Examen national de mathématiques SC (2022 Maroc)

Exercice 1 (3pts)

Dans l'espace rapporté à un repère orthonormé direct (O;i^→;j^→;k^→), on considère les points A(0;1;1), B(1;2;0) et C(-1;1;2).

(0.5) 1) a) Montrer que AB^→∧AC^→=i^→+k^→
(0.25) b) En déduire que x+z-1=0 est une équation cartésienne du plan (ABC).
(0.5) 2) Soit (S) la sphère de centre Ω(1;1;2) et de rayon R=√2
Déterminer une équation de phère (S).

(0.5) 3) Montrer que le plan (ABC est tangente à la sphère (S) au point A. 4) On considère la droite (Δ) passant par le point C est et perpendiculaire au plan (ABC)
(0.25) a) Déterminer une représentation paramétrique de la droite (Δ).
(0.5) b) Montrer que la droite (Δ) est tangente à la sphère (S) en un point D dont on déterminera les coordonnées.
(0.5) c) Calculer le produit scalaire AC^→.(i^→+j^→), puis en déduire la distance d(A,(Δ)).

Exercice 2 (3pts)

Dans le plan complexe rapporté à un repère orthonormé direct (O;u^→;v^→), on considère le points A d'affixe a=-1-i√3 , le point B d'affixe b=-1+i√3 et la translation t de vecteur OA^→.

(0.5) 1) Prouver que l'affixe du point D image du point B par la translation t est d=-2.
(0.5) 2) On considère la rotation R de centre D et d'angle

(	2π	)
	3

Montrer que l'affixe du point C image du point B par la rotation R est c=-4.

(0.5) 3) a) Ecrire le nombre suivant sous forme trigonométrique.
(0.5) b) En déduire que

(	b-c	)² =	c-d
	a-c		b-d

4) Soient (Γ) le cercle de centre D et de rayon 2, (Γ') le cercle de centre O et de rayon 4 et M un point d'affixe z appartenant aux deux cercles (Γ) et (Γ').
(0.25) a) Vérifier que |z+2|=2.
(0.5) b) Vérifier que z+z=-8 (remarquer que |z|=4).
(0.75) c) En déduire que les cercles (Γ) et (Γ') se coupent en un point unique qu'en déterminera.

Exercice 3 (3pts)

Une urne contient dix boules: trois boules blanches, trois boules vertes et quatre boules rouges indisernables au toucher. On tire au hasard simultanement trois boules de l'urne.

(0.75) 1) Montrer que

p(A) =	1
	6

où A est l'évènement "N'oubtenir aucune boule rouge".

(0.75) 2) Calculer p(B) où B est l'évènement "Obtenir tois boules blanches ou trois boules vertes".
3) Montrer que

p(C) =	1
	2

ou C est l'évènement "Obtenir exactement une boule rouge".
(0.75) 4) Calculer p(D) où D est l'évènement "Obtenir au moins deux boules rouges".

Exercice 4 (2.5pts)

On considère la fonction h définie sur IR par
h(x)=(x+1)e^x.

(0.75) 1) a) Vérifier que x→x^x est une primitive de la fonction h sur IR puis calculer

I =

-1 ∫ 0

h(x)dx

(0.75) b) A l'aide d'une intégration par parties calculer

J =

-1 ∫ 0

(x+1)²exdx

(0.5) 2) a) Résoudre l'équation différentielle (E): y"-2y'+y=0
(0.5) b) Montrer que la fonction h est la solution de (E) qui vérifie les conditions h(0)=1 et h'(0)=2.

Problème (8pts)

On considère la fonction numérique f définie sur IR par
f(x)=x(e^x/2 - 1)² et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→)(unité:1cm).

(0.5) 1) Calculer

lim +∞

f(x)

et

lim -∞

f(x)

(0.5) 2) Calculer et interprèter géométriquement le résultat.

lim +∞	f(x)
	x

(0.5) 3) a) Montrer que la droite (Δ) d'équation y=x est asymptote à la courbe (C) au voisinage de -∞.
(0.75) b) Etudier le signe de (f(x)-x) pour tout x de IR et en déduire la position relative de la courbe (C) et la droite (Δ).
(0.5) 4) a) Montrer que
f'(x)=(e^x/2 -1)²+xe^x/2(e^x/2-1) pour x de IR.
(0.5) b) Vérifier que x(e^x/2-1)≥0 pour tout x de IR puis en déduire le signe de la fonction dérivée f' sur IR.
(0.75) c) Dresser le tableau de variations de la fonction f sur IR.

(0.5) 5) a) Montrer que

f"(x)=	1	ex/2g(x)
	2

où g(x)=(2x+4)e^x/2-x-4 pour tout x de IR.
(0.5) b) A partir de la courbe c-dessous de la fonction g, déterminer le signe de g(x) sur IR (Remarque: g(α)=0).
(0.5) c) Etudier la concavité de la courbe (C) et déterminer les abscisses des deux points d'inflexions.

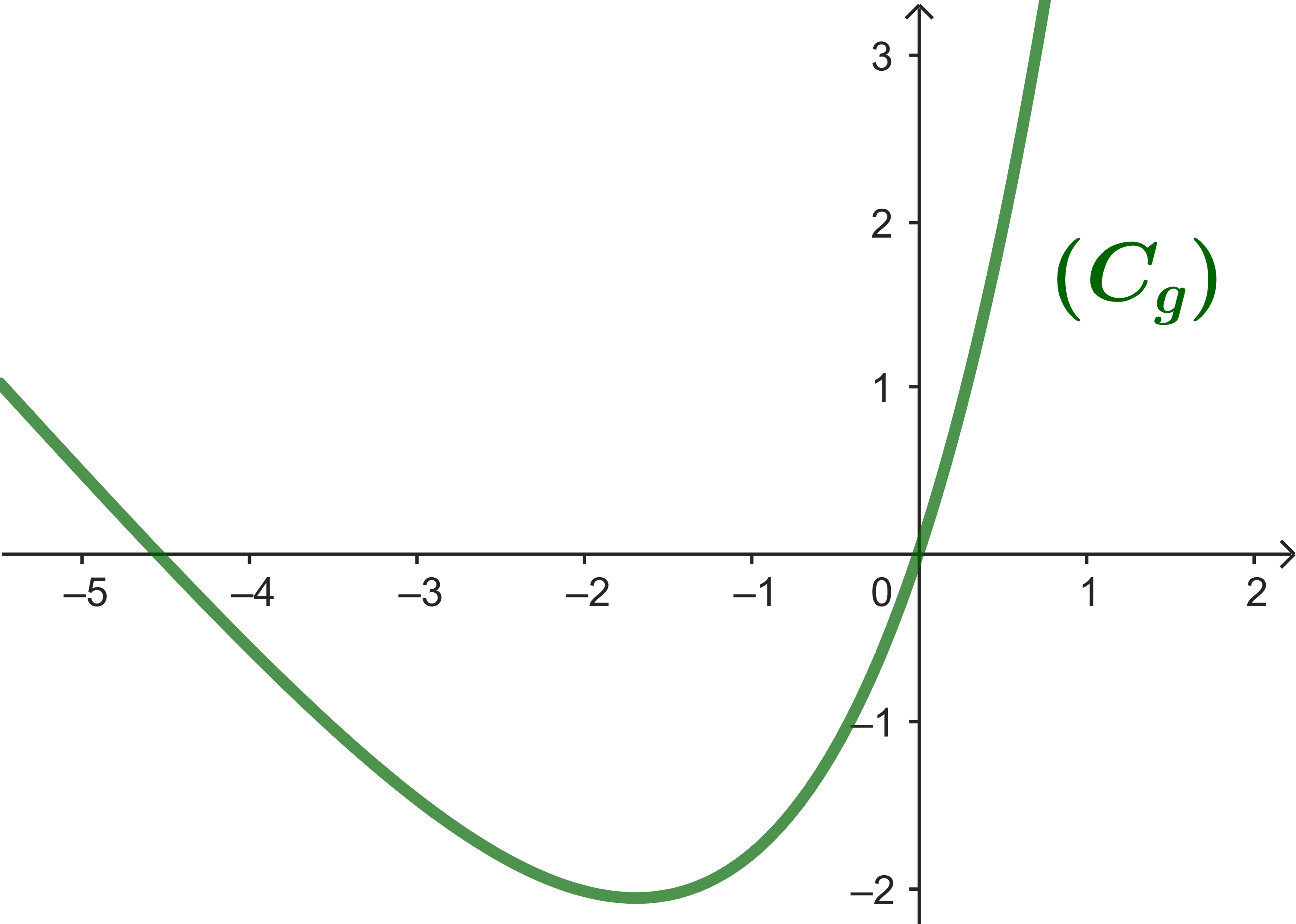
(1) 6) Construire la courbe (C) dans le repère (O;i^→;j^→)
(On prend: ln4=1,4 , α=-4,5 et f(α)=-3,5).

(0.5) 7) a) Montrer que la fonction f admet une fonction réciproque f^-1définie sur IR.
(0.25) b) Calculer (f^-1)'(ln4).
8) Soit (u_n) la suite numérique définie par u₀ et u_n+1=f(u_n) pour n de IN.
(0.5) a) Montrer par récurrence que 0< u_n< ln4 pour tout n de IN.
(0.5) b) Montrer que la suite (u_n) est décroissante.
(0.25) c) En déduire que la suite (u_n) est convergente.
(0.5) d) Calculer la limite de la suite (u_n).