Dérivabilité (1)
1- Dérivabilité
1.1 Dérivabilité en un point
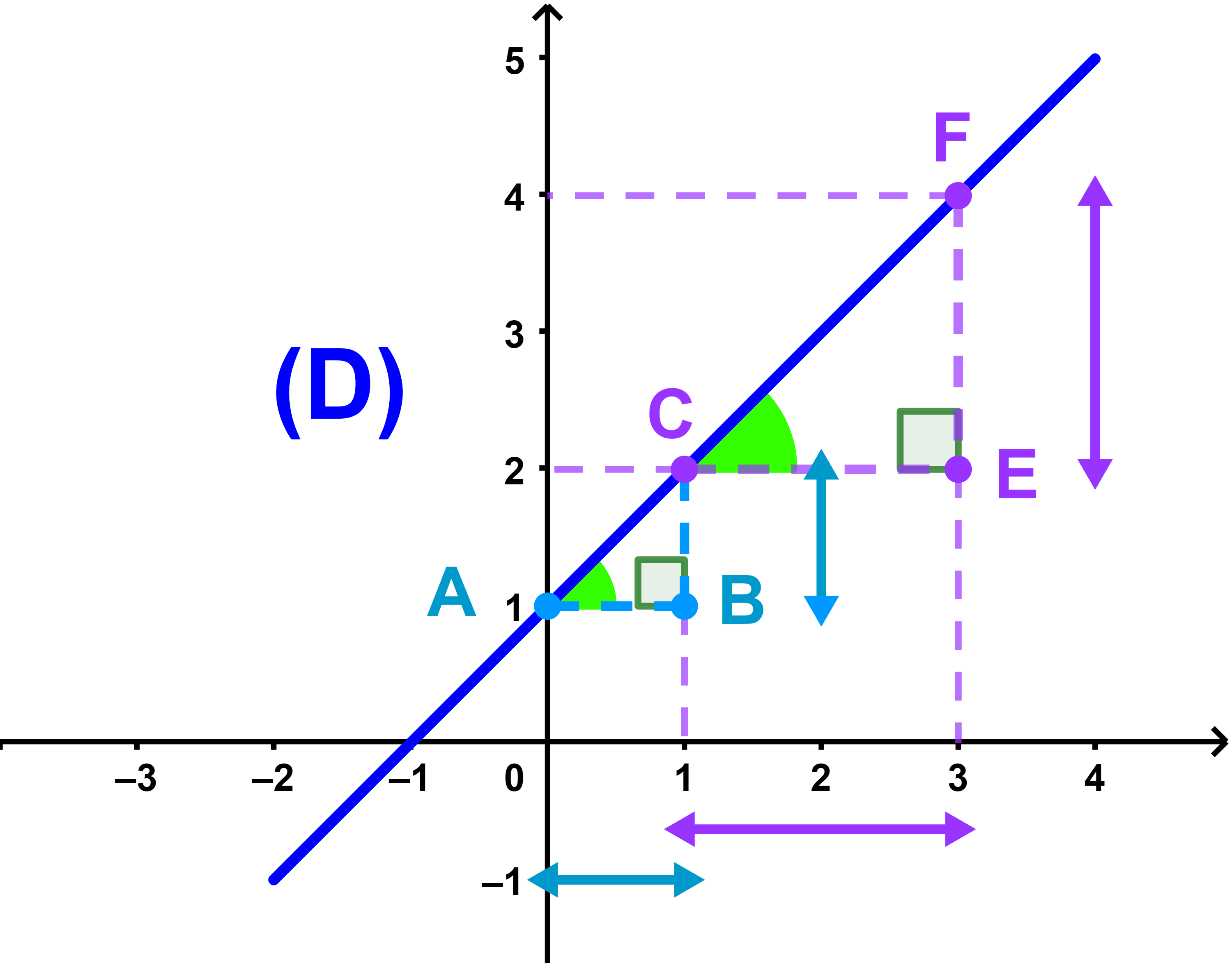
1.1.1 Coefficient directeur d'une droite
Soient A et B deux points différents d'une droite (D). le rapport
| m = | yC - yA |
| xC - xA |
est le Coefficient directeur de la droite (D).
y=mx+p est l'équation réduite de la droite (D).
p est l'ordonnée à l'origine.
Définition
Soit f est une fonction définie sur un intérvalle I et a∈I.
f est dérivable au point a signifie qu'il existe
un nombre réel L tel que
lim x→a |
f(x)-f(a) | = L |
| x-a |
L est le nombre dérivé de la fonction f en a, noté f'(a).
lim x→a |
f(x)-f(a) | = f '(a) |
| x-a |
Intérprétation graphique et équation de la tangente
Soit f une fonction dérivable au point a et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
Si M(x;y)∈(C) alors le nombre
lim x→a |
f(x) - f(a) | = f '(a) | |
| x-a |
est le coefficient directeur de la droite (T) qui touche (C) au point A(a;f(a)).
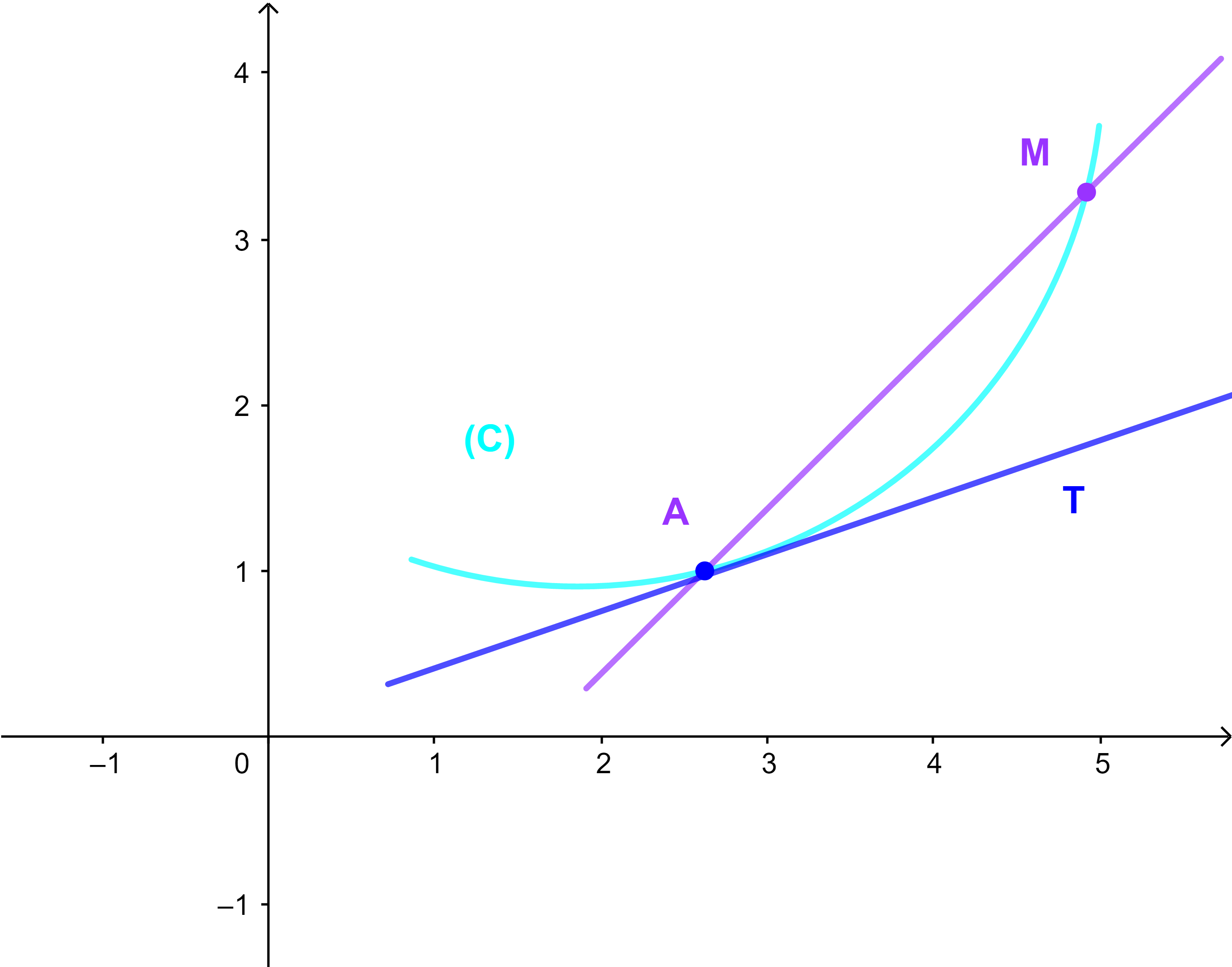
(T) est appelée tangent à (C) au point A
d'équation y=f'(a)(x-a)+f(a).
Propriété et définition
Soit f une fonction numérique définie sur un intervalle I tel que a∈I et (C) la courbe représentative de f dans un repère.
Si f est dérivable au point a alors la courbe (C) admet une tangente (T) au point A(a;f(a)).
L'quation y=f'(a)(x-a)+f(a) est appelée équation de la tangente (T). .
Exemple
Soit f une fonction numérique définie par f(x)=x².
montrer que f est dérivable au point 5 puis déterminer l'équation de la tangente au point d'abscisse 5.
Correction
1) On a (5∈D) et f(5)=5²=25.
lim x→5 |
f(x) - f(5) | = | lim x→5 |
x² - 25 |
| x-5 | x-5 |
| = | lim x→5 |
(x-5)(x+5) |
| x-5 | ||
| = | lim x→5 |
x + 5 = 10 |
donc f est dérivable au point 5 et f'(5)=10.
Puisque f est dérivable au point 5 alors la courbe (C) admet une tangente (T) d'équation
y=f'(5)(x-5)+f(5)=10(x-5)+25
ainsi (T): y=10x-25.