1- نهاية دوال اعتيادية عند +∞ وعند -∞ وعند 0

1.1 نهاية الدوال x→x² ; x→x³ ; x→xⁿ عند +∞ و عند 0

1.1.1 نشاط

اتمم الجدول واستنتج

x	..	10	10³	105	..	+∞
x²	0	...	...	...	..	...
x³	0	...	...	...	..	...

1.1.2 نتائج

1) كلما كبرت قيمة x كبرت قيمة x² واقتربت من لانهاية.
نقول ان نهاية x² عندما x يؤول الى +∞ هي +∞
ونكتب

lim x→+∞	x² = +∞

2) كلما كبرت قيمة x كبرت قيمة x³ واقتربت من لانهاية.
نقول ان نهاية x³ عندما x يؤول الى +∞ هي +∞ ونكتب

lim x→+∞	x³ = +∞

1.1.3 خلاصة

lim x→+∞	x = +∞		lim x→+∞	x³ = +∞
lim x→+∞	x² = +∞		lim x→+∞	xn = +∞ (n∈IN*)

ولدينا ايضا

lim x→0	x² = 0		lim x→0	x³ = 0

lim x→0	xn = 0	(n∈IN*)

1.2 نهاية الدوال x→x² و x→x³ عند -∞

1.2.1 نشاط

اتمم الجدول التالي واستنتج

x	-∞	..	-108	-104	10	0
x²	...	..	...	...	...	0
x³	...	..	...	...	...	0

1.2.2 نتائج

عندما x يصغر فان قيمة x³ تصغر وتقترب من - ∞.
نقول ان نهاية x³ عند -∞ هي -∞

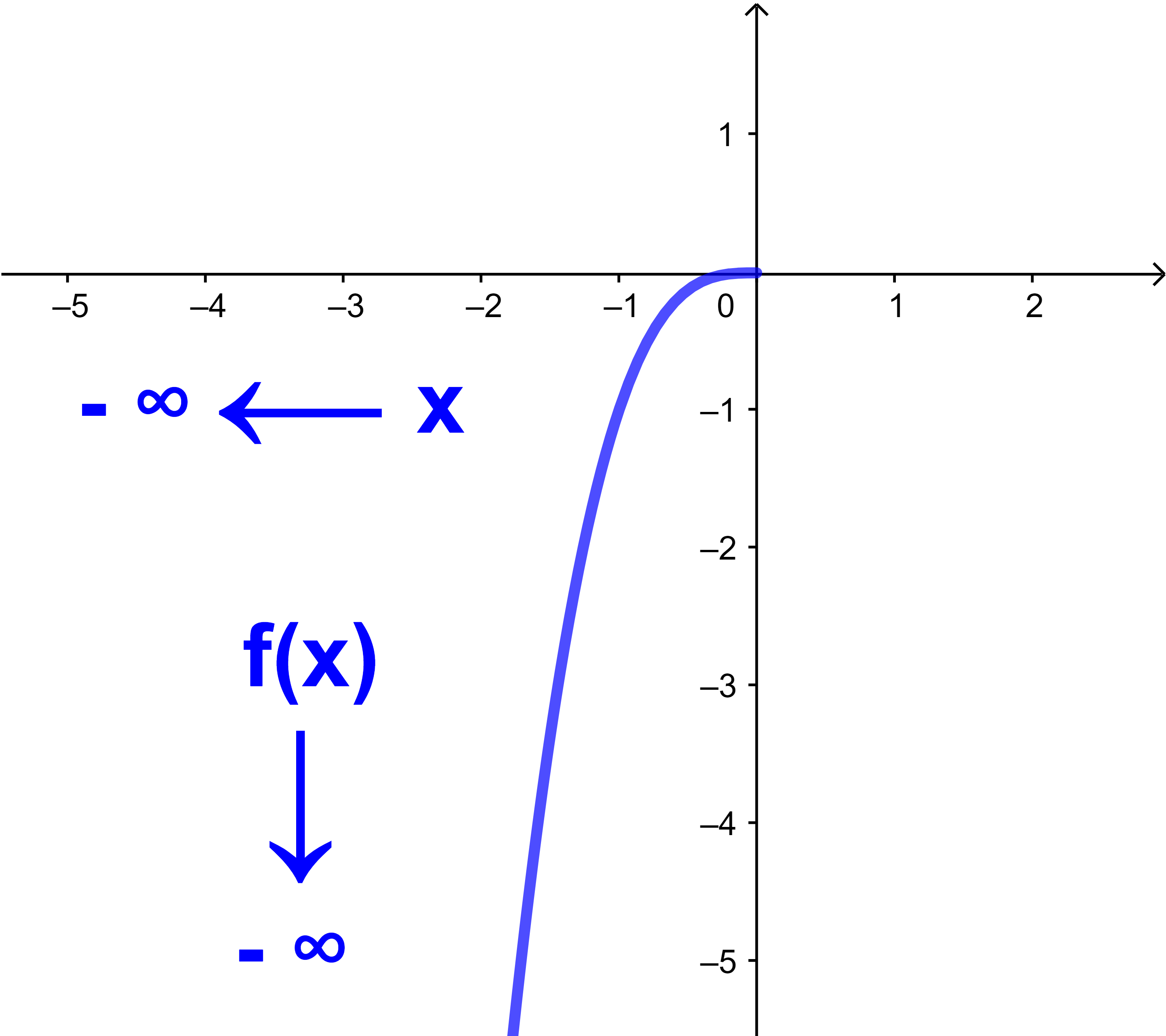
lim x→-∞	x³ = -∞	ونكتب

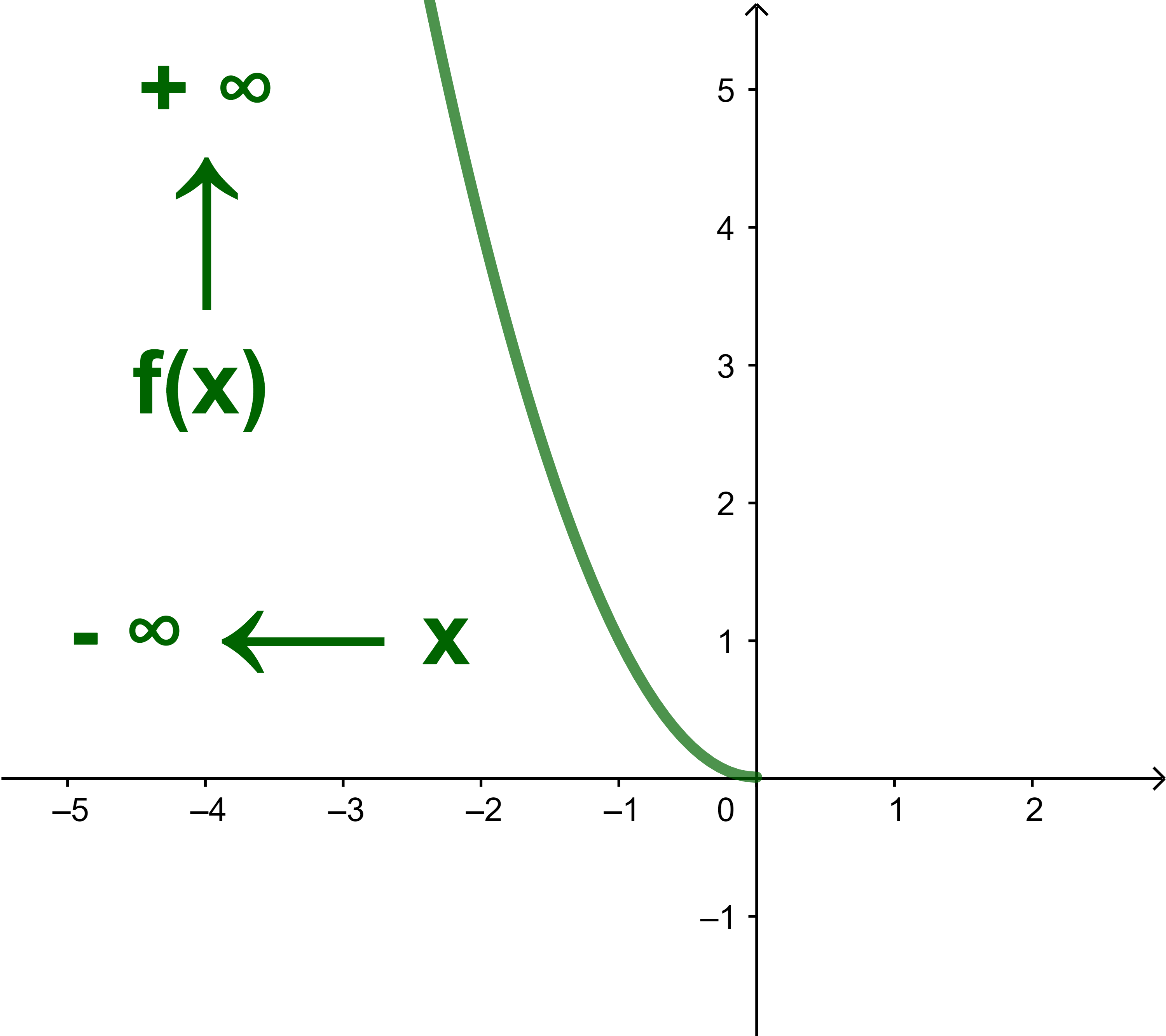
وعندما x يصغر فان قيمة x² تكبر وتقترب من +∞ ونكتب

lim x→-∞	x² = +∞

1.2.3 نتائج

lim x→-∞	x² = +∞
lim x→-∞	x³ = -∞

اذا كان n زوجي ويخالف 0 فان

lim x→-∞	xn = +∞

اذا كان n فردي ويخالف 0 فان

lim x→-∞	xn = -∞

أمثلة

lim x→-∞

x4 = +∞

lim x→-∞

x7 = -∞