2- دراسة دوال عددية

2.1 دراسة دوال اعتيادية للتذكير

2.1.1 مثال 1

لتكن f دالة عددية ذات المتغير x معرفة كما يلي
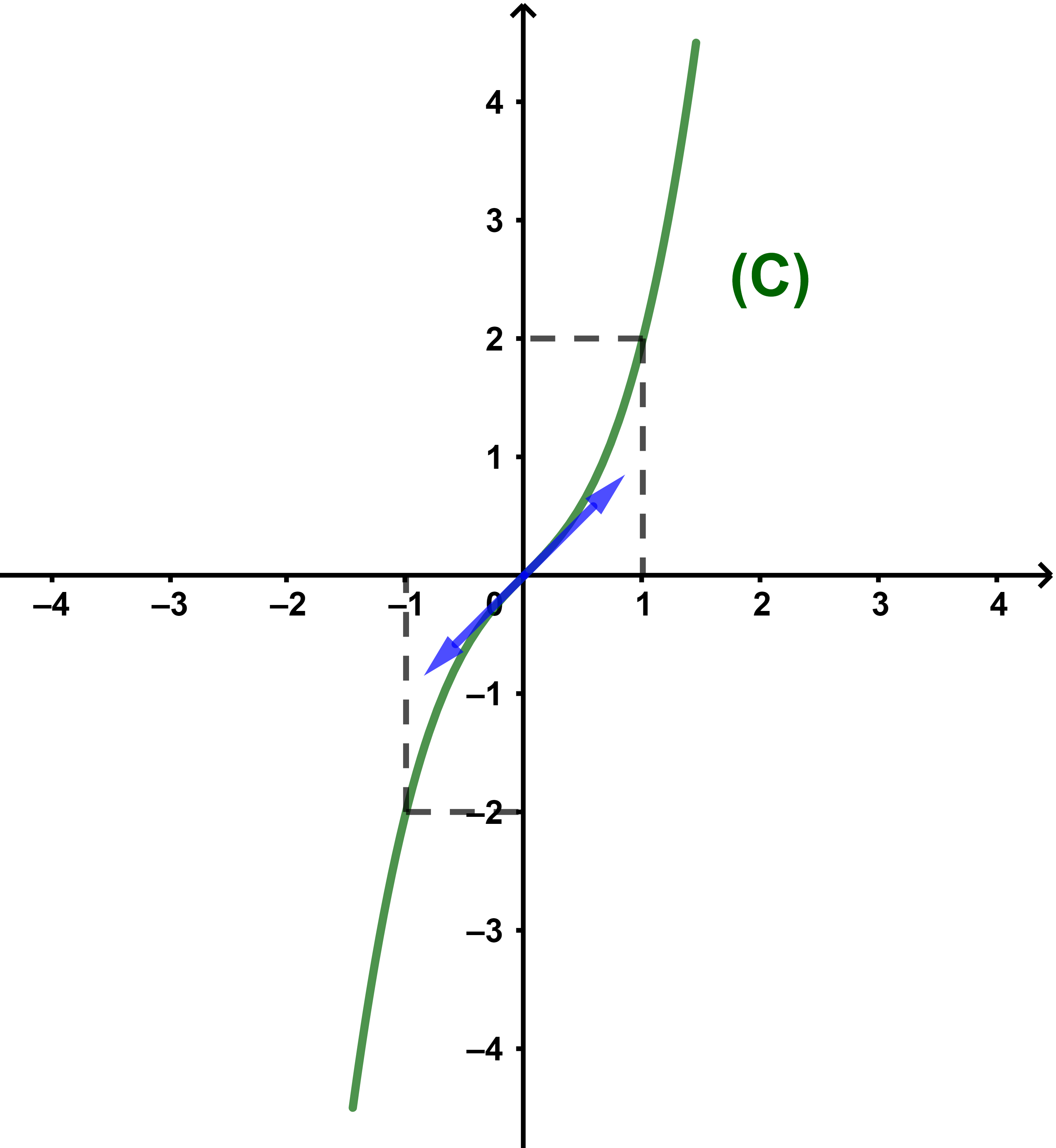
f(x)=x³+x و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) ادرس زوجية الدالة f واستنتج انه يكفي دراسة الدالة على المجال [0;+∞[.

2) احسب النهايتين التاليتين

lim - ∞

f(x)

lim + ∞

f(x)

3) احسب f'(x) حيث x∈D.
4) ادرس رتابة الدالة f وانشئ جدول تغيراتها.
5) (a) حدد معادلة المماس للدالة f عند النقطة 0.
(b) انشئ (C).

تصحيح
1) لدينا f حدودية اذن D=IR
ومنه فان لكل x∈IR لدينا -x∈IR.

ليكن x∈IR.
f(-x)=(-x)³+(-x)
=-x³-x=-(x³+x)
اذن لكل x∈IR لدينا f(-x)=f(x).
الدالة f اذن فردية ومنحنى الدالة f مماثل بالنسبة لأصل المعلم O وبالتالي يمكن دراسة الدالة على المجال E=[0;+∞[ ويسمى حيز المختصر للدراسة.
2) حساب النهايات

lim - ∞

f(x)

=

lim - ∞

x³ = - ∞

f دالة فردية اذن

lim + ∞

f(x)

= + ∞

ويمكن الاجابة باستعمال الخاصية

lim + ∞

f(x)

=

lim + ∞

x³ = + ∞

3) f دالة حدودية اذن قابلة للاشتقاق على IR
ليكن x∈IR.
f'(x)=(x³+x)'=3x²+1
اذن لكل x∈IR لدينا f'(x)=3x² +1.

4) اشارة f'(x)
f'(x)=0 ⇔ 3x²+1=0 ⇔ 3x²=-1
وهذا غير ممكن اذن المشتقة f' لا تنعدم.
ليكن x∈IR.
3x²≥0 اذن 3x²+1>0
ومنه فان لكل x∈IR لدينا f'(x)>0.
اذن f تزايدية قطعا على IR.

جدول التغيرات

x		-∞		+∞
f '(x)			+
f		-∞	↗	+∞

5) (a) الدالة f قابلة للاشتقاق على IR وبالخصوص في 0
اذن منحنى الدالة f يقبل مماسا (T) في النقطة 0
معادلته تكتب على الشكل y=f'(0)(x-0)+f(0).

لدينا f(x)= x³+x اذن f(0)=0
ولدينا f'(x)=3x²+1
اذن f'(0)=3.0²+1=1
ومنه فان معادلة المماس (T): y=x.
(b) منحنى الدالة f.
لرسم المنحنى (C) يكفي تعيين قيم افاصيل مناسبة لبعض النقط لمعرفة شكل المنحنى.