2- Etude des fonctions numériques

2.1 Etude des fonctions usuelles

2.1.1 Exemple 1

Soit f une fonction numérique définie par
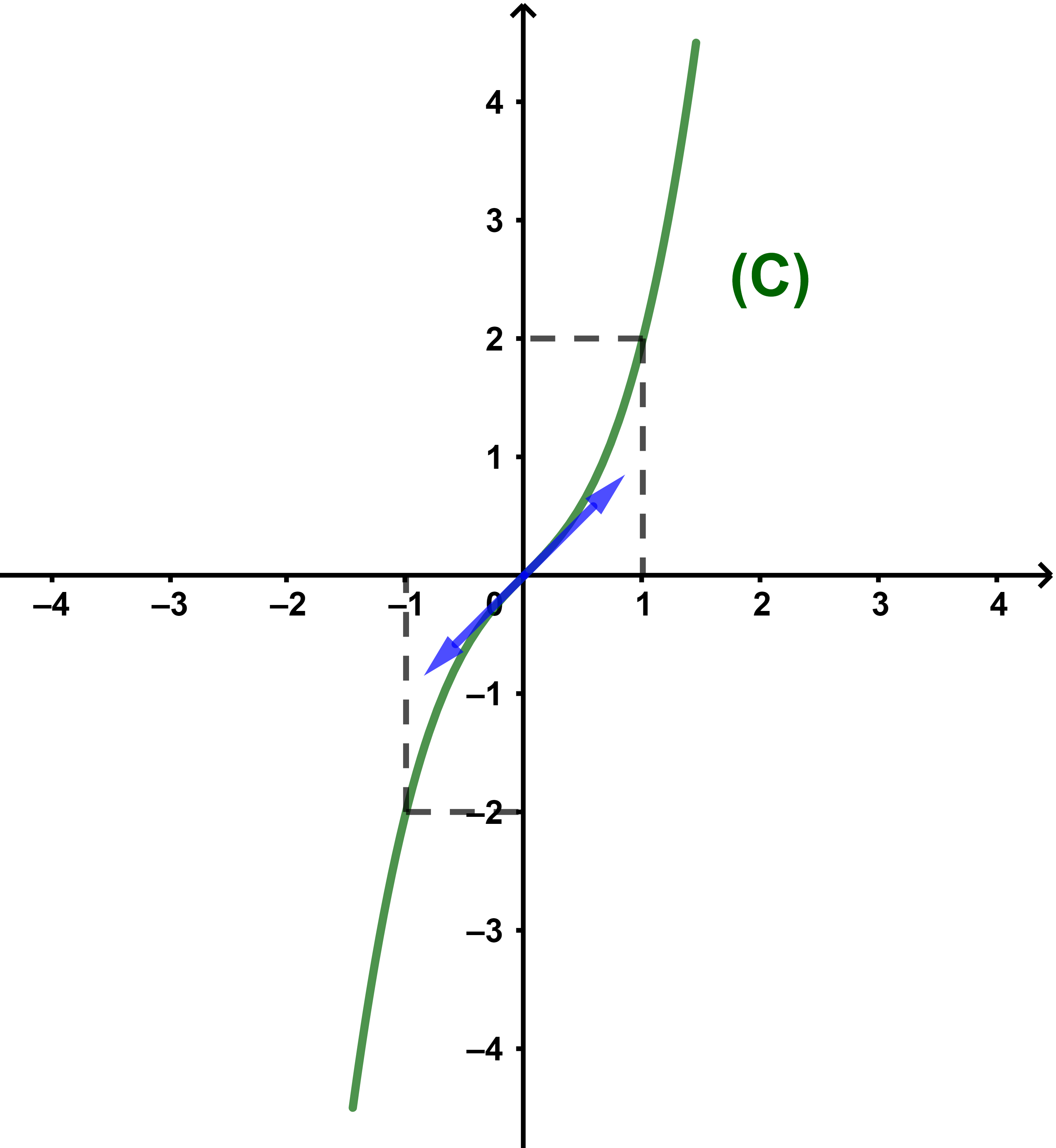
f(x)=x³+x et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
1) Etudier la parité de f et déduire qu'il suffit de l'étudier sur [0;+∞[.

2) Calculer les deux limites suivantes

lim - ∞

f(x)

lim + ∞

f(x)

3) Calculer f'(x) tel que x∈D.
4) Etudier la monotonie de f et tracer son tableau de variations.
5) Déterminer l'équation de la tangente au point 0 et tracer (C).

Correction
1) f est un polynôme donc D=IR
ainsi pour tout x∈IR on a -x∈IR.

Soit x∈IR
f(-x)=(-x)³+(-x)=-x³-x=-(x³+x).

donc pour tout x∈IR on a f(-x)=-f(x)
alors f est une fonction impaire et par conséquent la courbe (C) est symétrique par rapport à O.
Et donc il suffit d'étudier f sur l'intervalle [0;+∞[ et est appelé Domaine réduit d'étude.
2) Limites

lim - ∞

f(x)

=

lim - ∞

x³ = - ∞

Puisque f est impaire alors

lim + ∞

f(x)

= + ∞

Ou autrement

lim + ∞

f(x)

=

lim + ∞

x³ = + ∞

3) f est un polynôme donc dérivable sur IR.
Soit x∈IR.
f'(x)=(x³+x)'=3x²+1
donc pour tout x∈IR on a f'(x)=3x²+1.
4) Signe de f'(x).
f'(x)=0 ⇔ 3x²+1=0 ⇔ 3x²=-1
et ce n'est pas possible
donc f' ne s'annule pas.

Soit x∈IR
3x²≥0 donc 3x²+1>0
ainsi pour tout x∈IR on a f'(x)>0
f est donc strictement croissante sur IR.
Tableau de variations de f

x		-∞		+∞
f '(x)			+
f		-∞	↗	+∞

5) (a) f est dérivable sur IR et en particulier au point 0
donc la courbe (C) admet une tangente (T) au point d'abscisse 0 d'équation
y=f'(0)(x 0)+f(0)
On a f(x)=x³+x donc f(0)=0
et on a f'(x)=3x²+1
donc f'(0)=3.0²+1=1
ainsi (T): y=x.

(b) La courbe (C)