Exercice 1 tp

1) Soit f une fonction numérique définie par
f(x)=-2x²+4x+1 et (C_f) sa courbe reprèsentative dans un repère orthonormé (O;i^→;j^→).
(a) Calculer les deux limites suivantes

lim - ∞

f(x)

lim + ∞

f(x)

(b) Calculer f'(x) pour x∈D
(c) Etudier la monotonie de f et tracer son tableau de variations.
(d) Déduire un extremum de f.

2) Soit g une fonction numérique définie par
g(x) = x² -4 x+ 5 et (C_g) sa courbe reprèsentative
a) Calculer les deux limites suivantes

lim - ∞

g(x)

lim + ∞

g(x)

(b) Calculer f'(x) pour x∈D
(c) Etudier la monotonie de f et tracer son tableau de variations.
(d) Déduire un extremum de f.
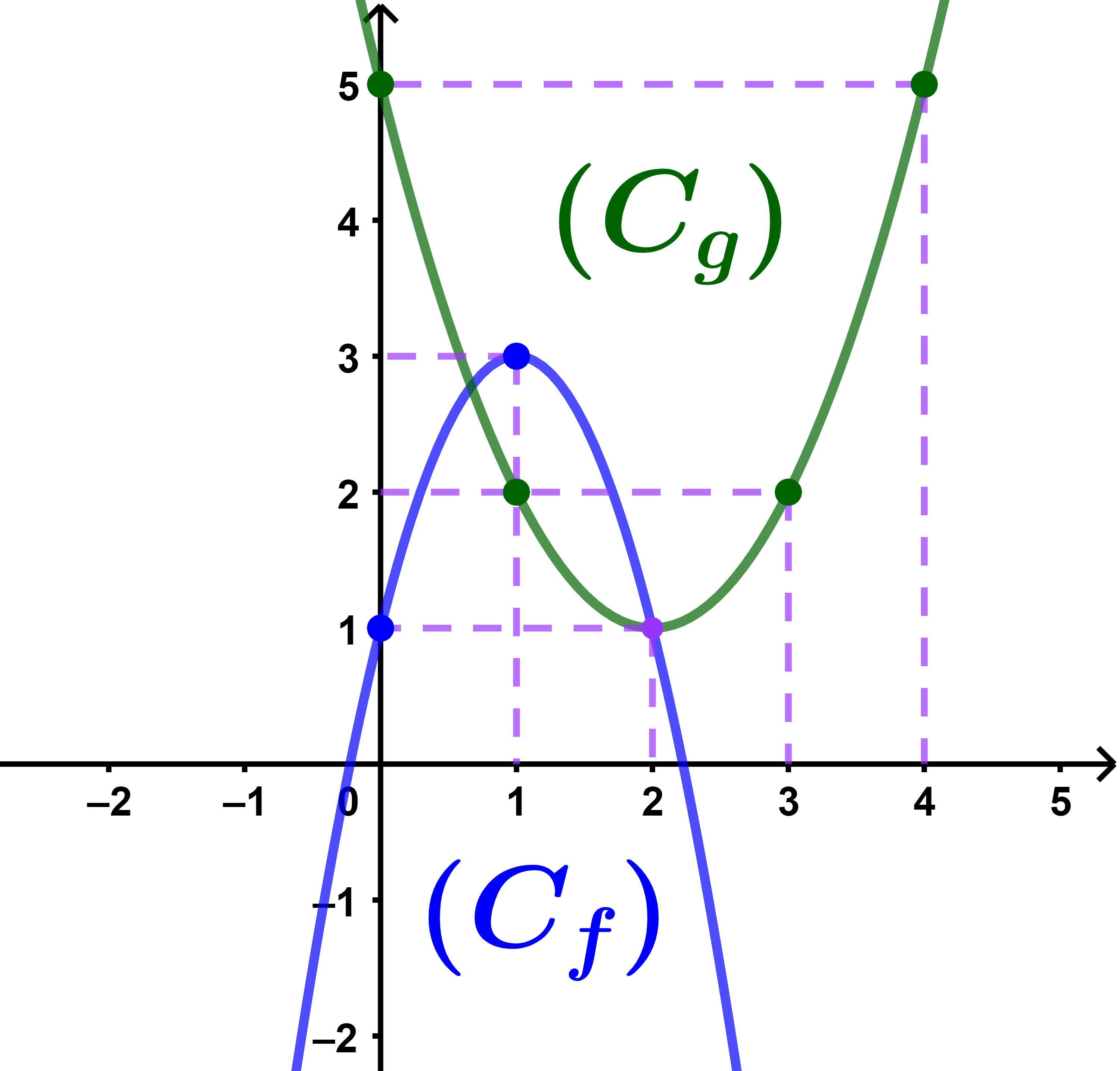
3) Construire les deux courbes (C_f) et (C_g) sur le même repère et résoudre graphiquement l'équation f(x)=g(x).

Correction

1) (a) On a f est un polynôme donc D=IR.

lim - ∞	f(x)	=	lim - ∞	- 2x² = - ∞
lim + ∞	f(x)	=	lim + ∞	- 2x² = - ∞

(b) f est un polynôme donc dérivable sur IR.

Soit x∈IR
f'(x)=(-2x²+4x+1)'=-4x+4
donc (∀x∈IR) f'(x)=-4x+4.

(c) Signe de f'(x)
f'(x)=0 ⇔ -4x+4=0
⇔ 4x=4 ⇔ x=1
f'(x) est de la forme ax+b et a=-4<0

x		-∞		1		+∞
- 4x + 4			+	0	-

Si x∈]-∞;1[ alors f'(x)>0
Si x∈]1;+∞[ alors f'(x)<0
et donc f est strictement croissante sur ]-∞;1] et strictement décroissante sur [1;+∞[.

Tableau de variations de f

x		-∞		1		+∞
f '(x)			+	0	-
f		-∞	↗	3	↘	-∞

(d) On a f'(1)=0 et f' change de signe de (+) à (-) donc f admet une valeur maximale f(1)=3.

2) (a) On a g est un polynôme donc D_g=IR.

lim - ∞

g(x)

=

lim - ∞

x² = + ∞

lim + ∞

g(x)

=

lim + ∞

x² = + ∞

(b) g est un polynôme donc dérivable sur IR. Soit x∈IR
g'(x)=(x²-4x+5)'=2x-4

(c) Signe de g'(x)
g'(x)=0 ⇔ 2x-4=0 ⇔ x=2
g'(x) est de la forme ax+b et a=2>0

x		-∞		2		+∞
2x - 4			-	0	+

Si x∈]-∞;2[ alors g'(x)<0

Si x∈]2;+∞[ alors f'(x)>0.

f est donc strictement décroissante sur ]-∞;2] et strictement croissante sur [2;+∞[.

x		-∞		2		+∞
g'(x)			-	0	+
g		+∞	↘	1	↗	+∞

(d) On a g'(2)=0 et g' change de signe de (+) à (-)
donc g(2)=1 est une valeur minimale.

3) Les courbes (C_f) et (C_g) se coupent en deux points donc l'équation f(x)=g(x) admet deux solutions l'un est 2 et l'autre compris entre 0 et 1.