Etude des fonctions numériques (11)
Exercice 1 tp
(I) On considère une fonction f définie par
| { | f(x) = | √(x)-1 | si x≠1 |
| x-1 | |||
| f(1) = | 1 | si x=1 | |
| 2 |
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) (a) Déterminer le domaine de définition de f.
2) Calculer la limite de f en +∞ et déduire une asymptote à la courbe (C).
3) Etudier la dérivabilité de f aux points 0 et 1.
4) Montrer que (∀x∈D\{0})
| f '(x) = | -1 | (f(x))² |
| 2√(x) |
et déduire la monotonie de f et tracer son tableau de variations.
5) Tracer la courbe (C).
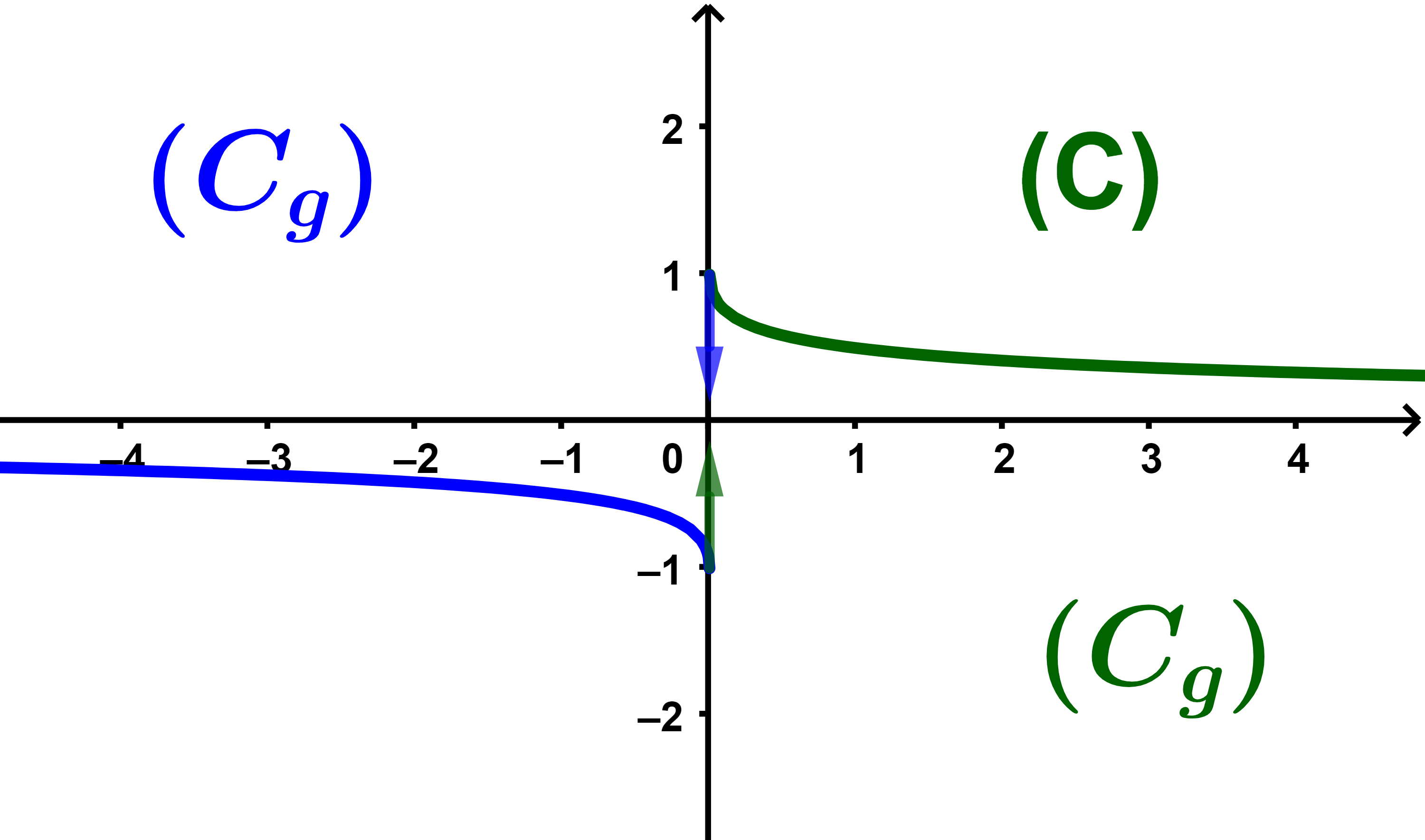
(II)) Soit g une fonction impaire et g(x)=f(x) sur D.
Tracer (Cg) sur le même repère.
Correction
(I) 1) (D={x∈IR/ f(x)∈IR}
={x∈IR/ x≥0 et x≠1}∪{1}=[0;+∞[.
2) LImite de f en +∞
lim +∞ |
f(x) = | lim +∞ |
√(x)-1 | |
| x-1 | ||||
=lim +∞ |
x-1 | = | lim +∞ |
1 |
| (x-1)(√(x)+1) | (√(x)+1) |
| Donc | lim +∞ | f(x) = 0 |
Ainsi la courbe (C) admet une asymptote horizontale d'équation y=0.
3) Dérivabilité en 0. On a f(0)=1
lim 0+ | f(x)- 1 | = | lim 0+ |
√(x)-x+1 |
| x-0 | x(x-1) |
| = | 1 | = -∞ |
| 0- |
et cela signifie que f n'est pas dérivable au point 0 et de plus la courbe (C) admet une demi-tangente verticale au point O(0;0).
Dérivabilité en 1
lim 1 | f(x) - | 1 |
| 2 | ||
| x-1 | ||
| = | lim 1 |
2√(x)-x-1 | |
| 2(x-1)² | |||
| = | lim 1 |
-(√²(x)-2√(x)+1²) | |
| 2(x-1)² | |||
| = | lim 1 |
-(√(x)-1)² | |
| 2(√(x)-1)²(√(x)+1)² |
| = | lim 1 |
-1 | = | -1 |
| 2(√(x)+1)² | 8 |
donc f est dérivable au point 1.
4) Les fonctions u:x→√(x)-1 et v:x→x-1 sont dérivables sur ]0;+∞[\{1} et v ne s'annule pas donc f est dérivable sur ]0;+∞[\{1}.
On a f est dérivable au point 1 donc f est dérivable sur D\{0}. Soit x∈D\{0}
| f '(x) = | (√(x)-1)'(x-1)-(√(x)-1).1 |
| (x-1)² |
| = | (x-1)-2√(x)(√(x)-1) |
| 2√(x)(x-1)² | |
| = | x-1-2x+2√(x) |
| 2√(x)(x-1)² |
| = - | (√(x)-1)² | = | -1 | f(x)² |
| 2√(x)(x-1)² | 2√(x) |
donc (∀x∈D\{0)}): f'(x)<0
ainsi f est strictement décroissante sur D\{0}.
| x | 0 | +∞ | |
| f'(x) | || | + | |
| f | 1 | ↘ |
0 |
(I-5) et (II) g est impaire donc sa courbe est symétrique par rapport à O.