Etude des fonctions numériques (15)
Exercice 1 tp
Soit f une fonction définie par
| f(x) = | x |
| √(|x+1|) |
et (C) sa courbe dans un repère (O;i→;j→).
1) Déterminer D, le domaine de définition de f.
2) Calculer les limites suivantes
lim (-1) |
f(x) | lim 1+ |
f(x) |
lim -∞ |
f(x) | lim +∞ |
f(x) |
et déterminer une asymptote à (C).
2) Etudier la monotonie de f et tracer son tableau de variations.
3) Tracer la courbe (C) et résoudre graphiquement l'équation f(x)=m selon les valeurs de m.
Correction
1) D={x∈IR/ x+1≠0} =]-∞;-1[∪]-1;+∞[.
| { | f(x) = | x | si x< -1 |
| √(-x-1) | |||
| f(x) = | x | si x> -1 | |
| √(x+1) |
lim -∞ |
x | = | lim -∞ |
x√(-x-1) |
| √(-x-1) | -x-1 | |||
| = | lim -∞ |
x | lim -∞ |
√(-x-1) |
| -x-1 |
lim -∞ |
x | = | lim -∞ |
x | = | -1 |
| -x-1 | -x |
lim -∞ |
-x-1 = +∞ ⇒ | lim -∞ |
√(-x-1) = +∞ |
donc
lim -∞ |
f(x) | = - ∞ |
lim +∞ |
x | = | lim +∞ |
x√(x+1) |
| √(x+1) | x+1 |
| = | lim +∞ |
x | lim +∞ |
√(x+1) |
| x+1 |
lim +∞ |
x | = | lim +∞ |
x | = | 1 |
| x+1 | x |
lim +∞ |
x+1 = +∞ ⇒ | lim +∞ |
√(x+1) = +∞ |
donc
lim +∞ |
f(x) | = + ∞ |
|x+1|≥0 donc
lim (-1) |
|x+1| ≥0 ⇒ | lim (-1) |
√(|x+1|)≥0 |
lim -1 |
x | = | -1 | - ∞ |
| √(|x+1|) | 0+ |
donc
lim -1 |
f(x) = | = - ∞ |
ainsi (C) admet une asymptote d'équation x=-1.
On a
lim -∞ |
f(x) = - ∞ |
lim -∞ |
f(x) | = | lim -∞ |
x |
| x | x√(-x-1) |
lim -∞ |
-x-1 = +∞ ⇒ | lim -∞ |
1 | = 0 |
| √(-x-1) |
donc
lim -∞ |
f(x) | = 0 |
| x |
Ainsi (C) admet une branche parabolique de direction (Ox).
On a
lim +∞ |
f(x) = + ∞ |
lim +∞ |
f(x) | = | lim +∞ |
x |
| x | x√(x+1) |
lim +∞ |
x+1 = +∞ ⇒ | lim +∞ |
1 | = 0 |
| √(x+1) |
Donc
lim +∞ |
f(x) | = 0 |
| x |
ainsi (C) admet une branche parabolique de direction (Ox)
2) Monotonie de f sur I=]-∞;-1[
| f(x) = | x | si x< -1 |
| √(-x-1) |
La fonction x→x est dérivable sur I
donc f est dérivable sur I.
Soit x∈I
| f '(x) = | √(-x-1) - x(√(-x-1))' |
| (√(-x-1))² | |
| = | 2(√(-x-1))² + x |
| 2(-x-1)√(-x-1) |
donc
| f '(x) = | -x-2 |
| 2(-x-1)√(-x-1) |
f'(x) est de signe de -x-2.
f'(x)=0⇔ -x-2=0⇔x=-2.
f est strictement croissante sur ]-∞;-2]
et strictement décroissante sur [-2;-1[
Monotonie de f sur J=]-1;+∞[.
| f(x)= | x | si x> -1 |
| √(x+1) |
Soit x∈J
| f '(x) = | √(x+1) - x(√(x+1))' |
| (√(x+1))² |
| = | 2(√(x+1))² - x |
| 2(x+1)√(x+1) |
donc
| f'(x) = | x+2 |
| 2(x+1)√(x+1) |
f'(x) est de signe de x+2
f'(x)=0⇔ x+2=0⇔x=-2
-2∉I2 et x+2>0 donc f est strictement croissante
sur ]-1;+∞[.
| x | -∞ | -2 | -1 | +∞ | |||||
| f'(x) | + | 0 | - | + | |||||
| f | -∞ |
↗ |
-2 | ↘ |
-∞ |
-∞ |
↗ |
+∞ | |
3) La courbe (C)
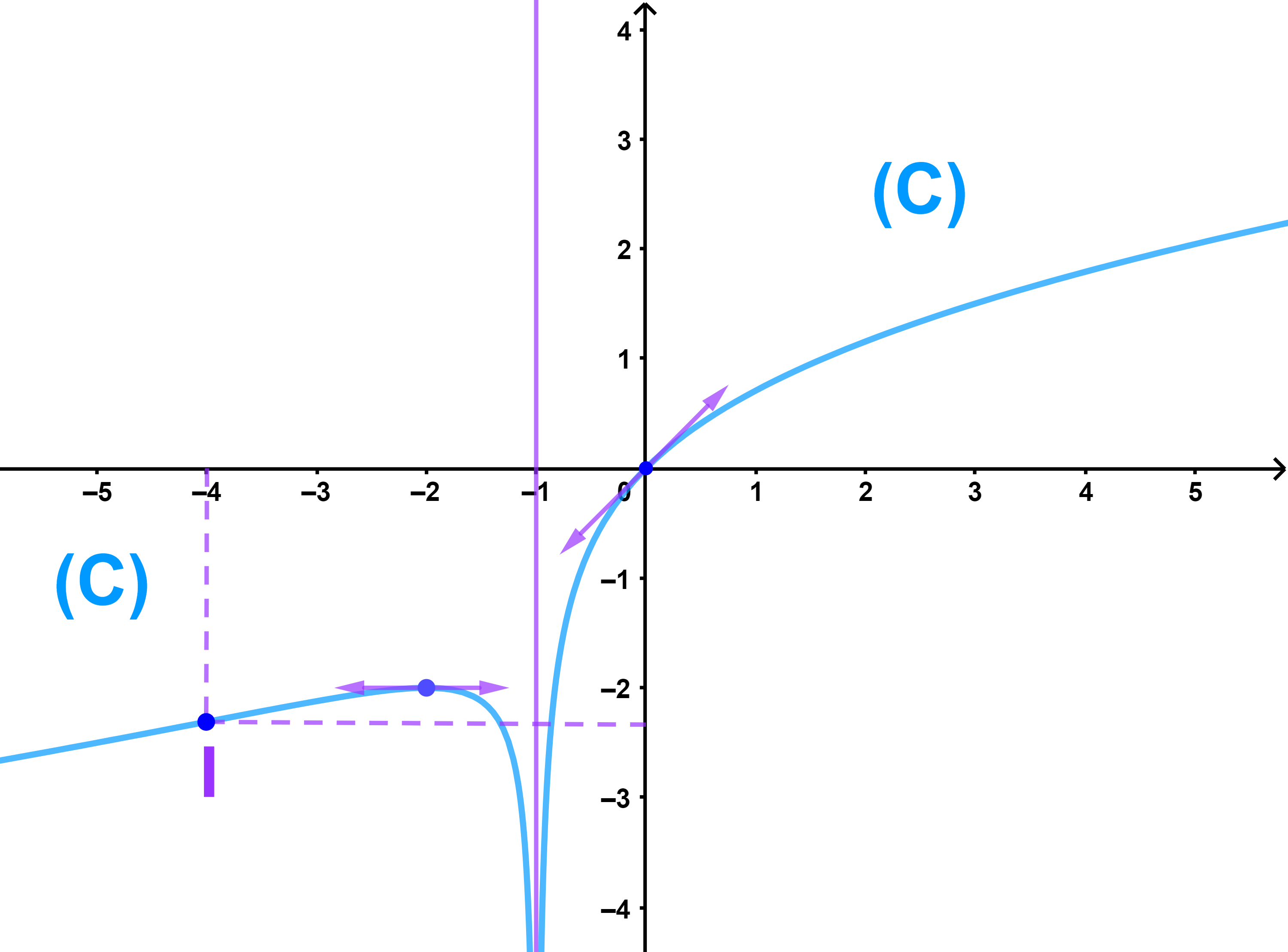
4) Résolutions graphique de (E): f(x)=m.
on considère la droite variante et paralléle à l'axe des ordonnées (Dm).
si m<-2 alors (Dm) coupe la courbe en trois points donc l'équation (E) admet trois solutions.
si m=-2 alors (Dm) coupe la courbe en deux points donc l'équation admet deux solutions.
si m>-2 alors (Dm) coupe la courbe en un seul point donc l'équation (E) admet une seule solution.