Etude des fonctions numériques (9)
Exercice 1 tp
Soit f une fonction numérique définie par
| f(x) = √(x+1)+ | 1 |
| √(x+1) |
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) Déterminer D, le domaine de définition de f.
2) Calculer les limites de f en +∞ et en -1 puis déterminer les branches infinies de (C).
3) Montrer que ∀x∈D
| f '(x)= | x |
| 2(x+1)√(x+1) |
et étudier son signe.
4) Tracer le tableau de variations de f.
5) tracer la courbe (C).
Correction
1) D={x∈IR/x+1≥0 et √(x+1)≠0} =]-1;+∞[.
2) Limite en +∞. On a
lim +∞ |
x+1 = +∞ |
| ⇒ | lim +∞ |
√(x+1) = +∞ |
| ⇒ | lim +∞ |
1 | = 0 |
| √(x+1) |
+∞ + 0 = +∞ donc
lim +∞ |
f(x) | = +∞ |
Limite de f en (-1)+
| x | -∞ | -1 | +∞ | ||
| x+1 | - | 0 | + |
lim (-1)+ |
1 | = | 1 | = +∞ |
| x+1 | 0+ |
| ⇒ | lim (-1)+ |
1 | = +∞ |
| √(x+1) |
lim (-1)+ |
f(x) = | lim (-1)+ |
√(x+1)+ | 1 |
| √(x+1) |
donc
lim (-1)+ |
f(x) = 0 + ∞ = + ∞ |
ainsi (C) admet une asymptote d'équation x=-1.
lim +∞ |
f(x) = +∞ |
lim +∞ |
f(x) | = | lim +∞ |
√(x+1) | + | 1 |
| x | x | x√(x+1) |
lim +∞ |
√(x+1) | = | lim +∞ |
√( | x+1 | ) |
| x | x² |
On a
lim +∞ |
x+1 | = | lim +∞ |
x |
| x² | x² |
| = | lim +∞ |
1 | =0 |
| x |
On a aussi
lim +∞ |
1 | = 0 |
| x√(x+1) |
Donc
lim +∞ |
f(x) | = 0 |
| x |
ainsi (C) admet une branche parabolique de direction l'axe des abscisses.
3) x→(x+1) est strictement positive et dérivable sur D donc f est dérivable sur D. Soit x∈D
| f '(x) = | 1 | - | (√(x+1))' |
| 2√(x+1) | (√(x+1))² |
| = | 1 | - | 1 |
| 2√(x+1) | (x+1)2√(x+1) |
donc
| f '(x) = | x |
| 2(x+1)√(x+1) |
f' est de signe de x donc f est strictement croissante sur IR+
et strictement décroissante sur
]-1;0].
4) Tableau de variations
| x | -1 | 0 | +∞ | ||||
| f'(x) | - | 0 | + | ||||
| f | +∞ | ↘ |
2 |
↗ |
+∞ | ||
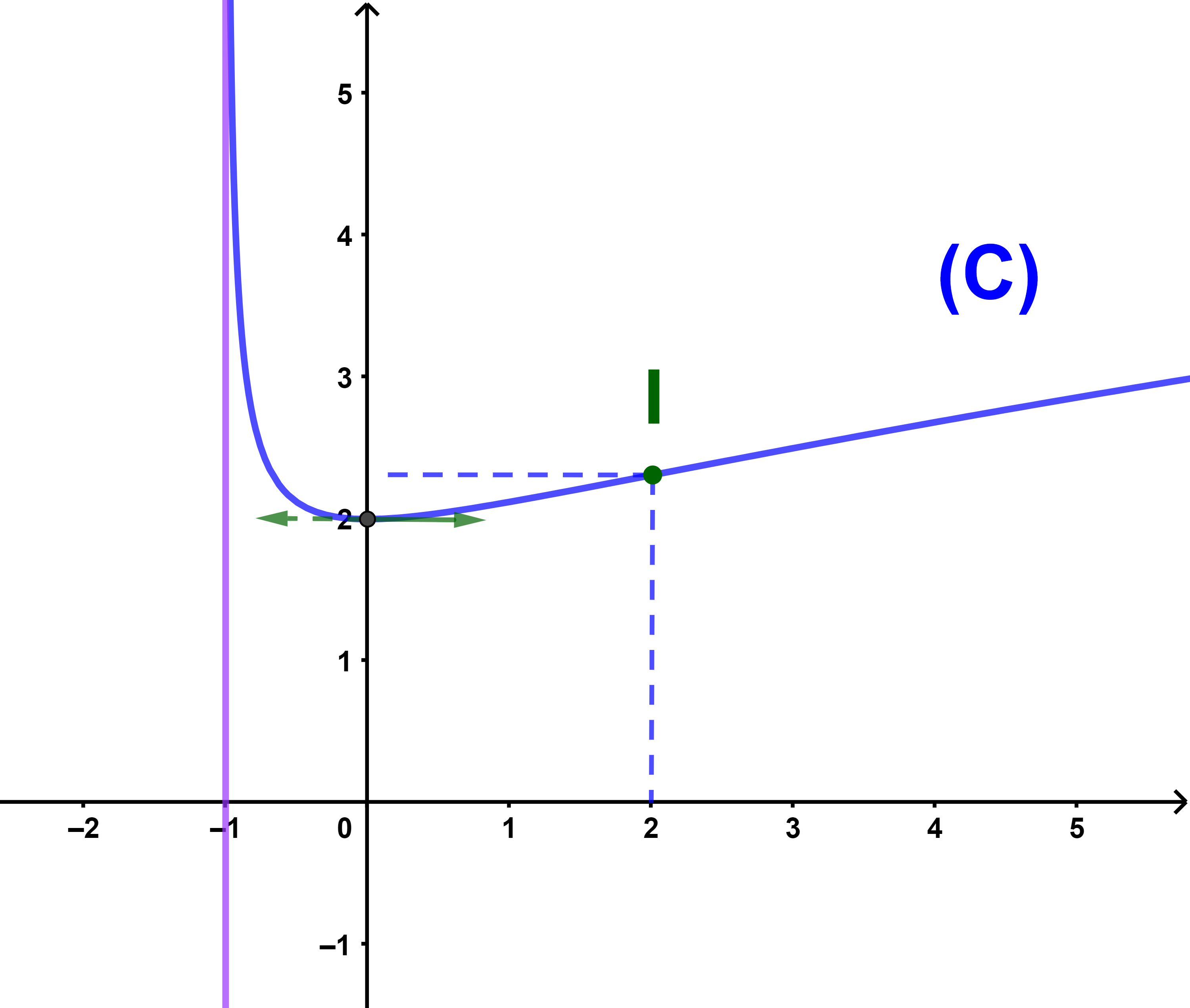
5) La courbe (C)