Exercice 1 tp

Soit f une fonction numérique définie par
f(x)= cos(x) + sin(2x).
Montrer que f est périodique de période 2π.

Correction

Les fonctions cosinus et sinus sont périodiques de période 2π.
La fonction h: x→sin(2x) est périodique de période π.

En effet
(1) (∀x∈IR) on a (x+π∈IR et x-π∈IR)
(2) Soit x∈IR.
h(x+π)=sin2(x+π)=sin(2x+2π)=sin(2x)
donc h(x+π)=h(x).
Puisque la période de la fonction cosinus est 2π alors la plus grande période T=2π qui doit être prise (car cos(x+π)≠cos(x)).

Soit x∈IR on a (∀x∈IR) x+π∈IR et x-π∈IR
f(x+2π)=cos(x+2π)+sin2(x+2π)
=cos(x)+sin(2x+4π)
=cos(x)+sin(2x)
donc (∀x∈IR): f(x+2π)=f(x).
ainsi f est périodique de période 2π.

1.2 Fonction bornée

1.2.1 Fonction majorée

Soit f une fonction définie sur un intérvalle I.
f est majorée sur I si
(∃M∈IR)(∀x∈I): f(x)≤M.

1.2.2 Fonction minorée

Soit f une fonction définie sur un intérvalle I.
f est minorée sur I si
(∃m∈IR)(∀x∈I): f(x)≥m.

1.2.3 Fonction bornée

Soit f une fonction définie sur un intérvalle I.
f est bornée sur I si
(∃m;M ∈IR)(∀x∈I): m≤f(x)≤M
ou encore
(f est bornée) ⇔ (∃α> 0)(∀x∈I): |f(x)|≤α.

Exercice

Soit f une fonction numérique définie par

Montrer que f bornée.

1.3 Comparaison de deux fonctions

1.3.1 Exemple

Soient f et g deux fonctions définies comme suit
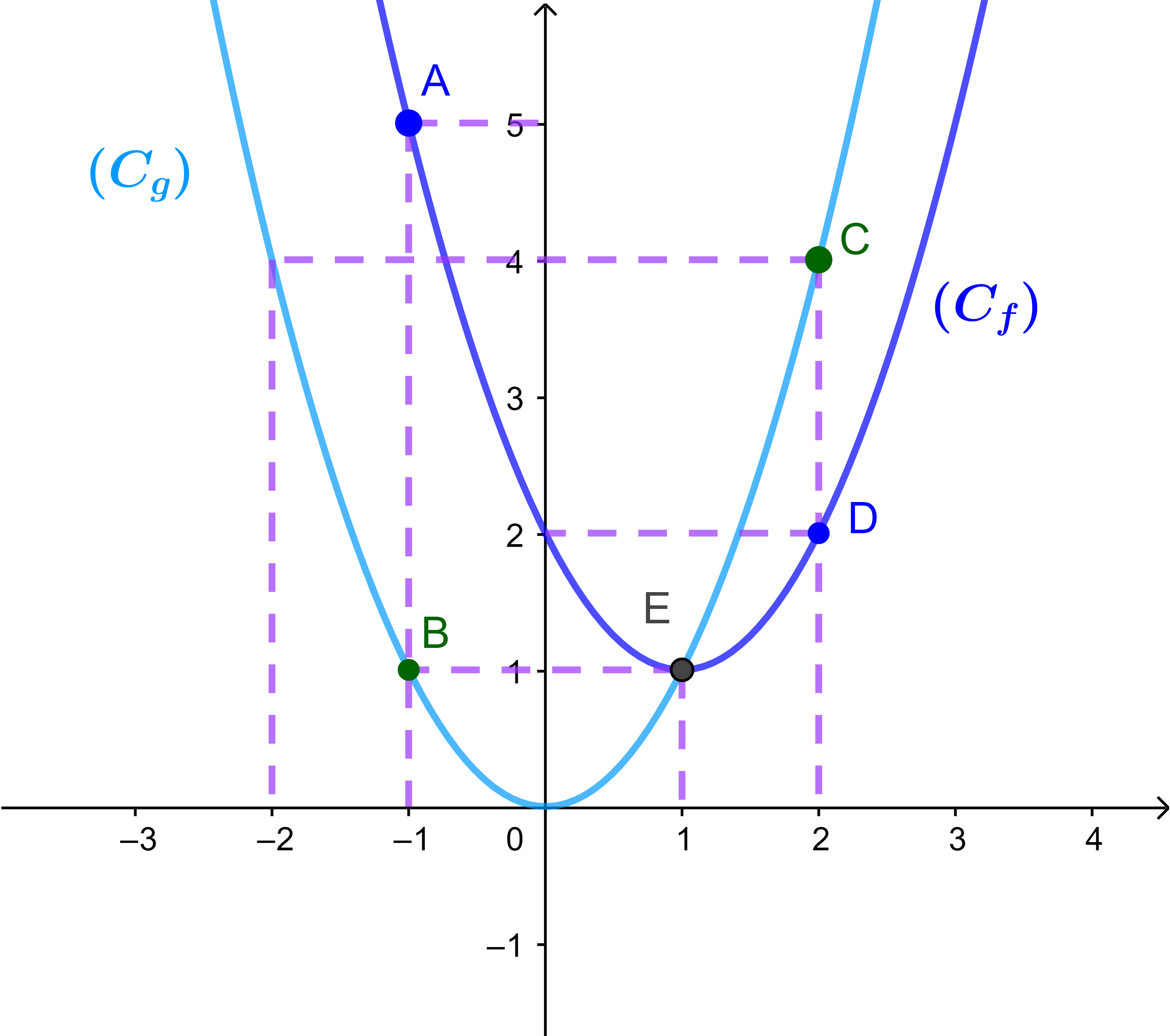
f(x)=x²-2x+1 et g(x) =x².
Tracer les courbes (C_f) et (C_g).
Comparer graphiquement et algébriquement f et g.

1.3.2 définition 1

On dit que f et g sont égales et on écrit f=g si les deux conditions suivantes sont vérifiées
1) D_f = D_g.
2) (∀x∈D): f(x)=g(x).

1.3.3 Définition 2

Soient f et g deux fonctions définies sur D.
f<g sur I⊂D si (∀x∈I): f(x)<g(x).
graphiquement: f<g signifie que la courbe (C_f) est au-dessous de la courbe (C_g) sur I.