Limite d'une fonction (1)
1- Limite des fonctions usuelles en ±∞ et en 0
1.1 Limite des fonctions usuelles en +∞ et en 0
1.1.1 Activité
Compléter le tableau et conclure.
| x | .. | 10 | 10³ | 105 | .. | +∞ |
| x² | 0 | ... | ... | ... | .. | ... |
| x³ | 0 | ... | ... | ... | .. | ... |
| √(x) | 0 | ... | ... | ... | .. | ... |
1.1.2 Résultats
Plus la valeur de x est élévée, plus la valeur de chacun de x² ; x³ et √(x) est élevée et se rapproche de l'infini.
On dit que +∞ est la limite de x² (ou x³ ou √(x)) quand x tend vers +∞ et on écrit
lim x→+∞ |
x² = +∞ | lim x→+∞ |
x³ = +∞ |
lim x→+∞ |
xn = +∞ (n∈IN*) | lim x→+∞ |
√(x) = +∞ |
On a aussi
lim x→0 |
x² = 0 | lim x→0 |
x³ = 0 |
lim x→0 |
xn = 0 (n∈IN*) | lim x→0 |
√(x) = 0 |
1.2 Limite des fonctions x→x² et x→x³ en -∞
1.2.1 Activité
Compléter le tableau et conclure.
| x | -∞ | .. | -108 | -104 | 10 | 0 |
| x² | ... | .. | ... | ... | ... | 0 |
| x³ | ... | .. | ... | ... | ... | 0 |
1.2.2 Résultats
1) Si x diminue
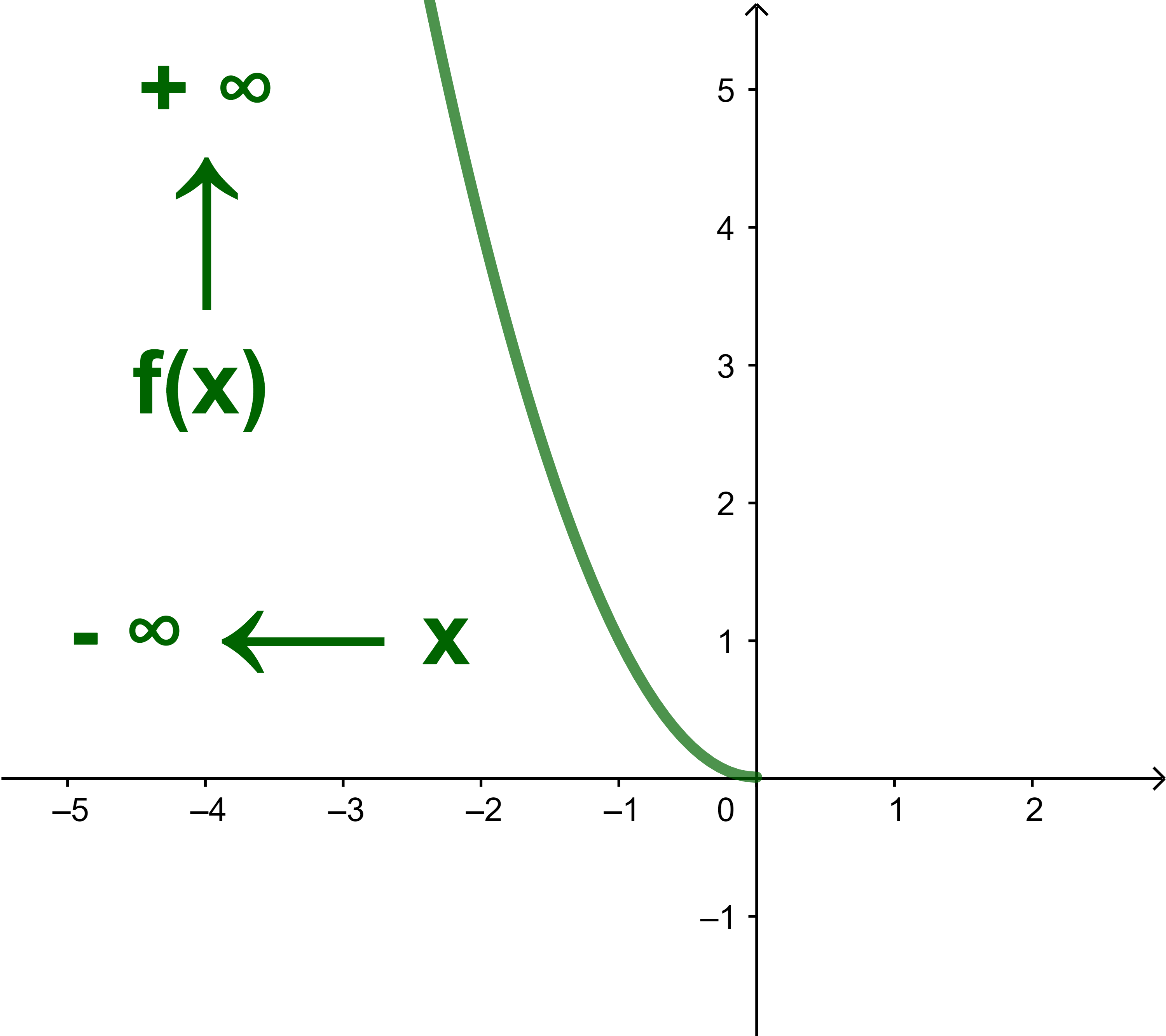
x² augmente et s'approche de +∞ et on écrit
lim x→-∞ |
x² = +∞ |
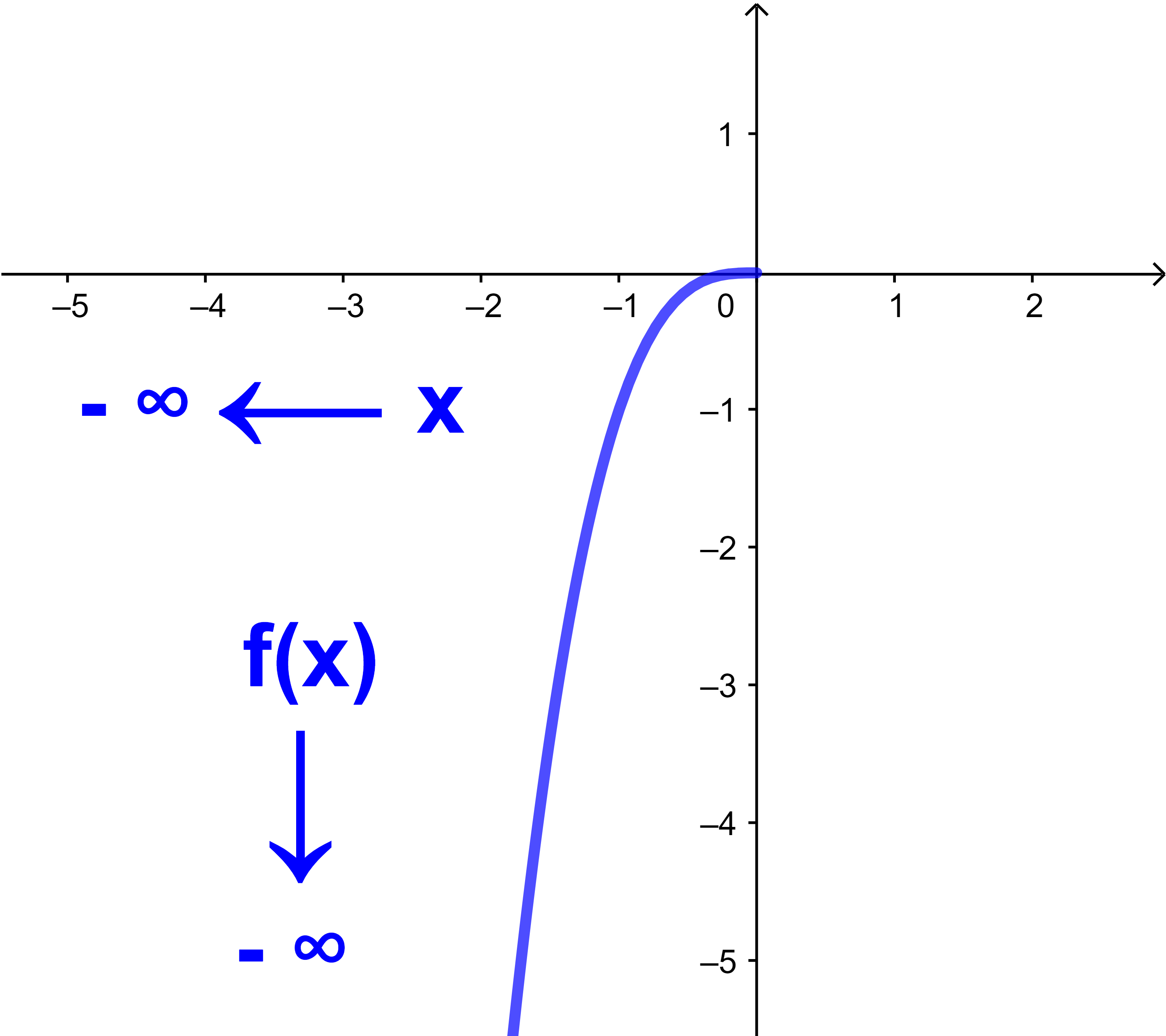
2) Si x diminue alors x³ diminue et s'approche de -∞.
On dit que -∞ est la limite de x³ quand x tend vers -∞
et on écrit
lim x→-∞ |
x³ = -∞ |
| Si n est pair et non nul | lim x→-∞ |
xn = +∞ |
| Si n est impair | lim x→-∞ |
xn = -∞ |
Exemples
lim x→-∞ |
x4=+∞ |
lim x→-∞ |
x7=-∞ |