مبادئ في المنطق (1)
تمرين 1 tp
حدد نفي كل من العبارات التالية
1. ∀x∈IR, x+1=10
2. ∃x∈IR, x+1=10
3. ∀x∈IR, x> 0
4.∃x∈IR, x≤2
تمرين 2 tp
اكتب العبارة التالية باستعمال المكممات
1. كل عدد نسبي له مقابل
2. ليس لكل عدد حقيقي مقلوبا
3. الجزء الصحيح لعدد حقيقي عدد صحيح نسبي
تمرين 3 tp
حدد نفي العبارات التالية
1) (∀x∈IR)(∃n∈IN) / n > x
2) (∀x∈IR)(∃n∈ℤ) / n≤ x < n+1
3) ∀(x;y)∈E²: f(x)=f(y) ⇒ x=y
4) ∀(x;y)∈IR²:
√(x²+1) + √(y²+1)=2 ⇔ (x=0) ∧ (y=0)
تمرين 4 tp
حل النظمة التالية :
| { | x²-4=0 |
| y=3 |
تصحيح
((x²-4=0)∧ y=3) ⇔([(x-2)(x+2)=0]∧y=3)
⇔ [(x=2∨x=-2)]∧y=3
⇔(x=2∧y=3)∨(x=-2∧y=3)
وبالتالي S={(2;3) ; (-2;3)}
تمرين 5 tp
حل النظمة التالية
| { | x²-4=0 |
| (y-1)(y+3)=0 |
تمرين 6 tp
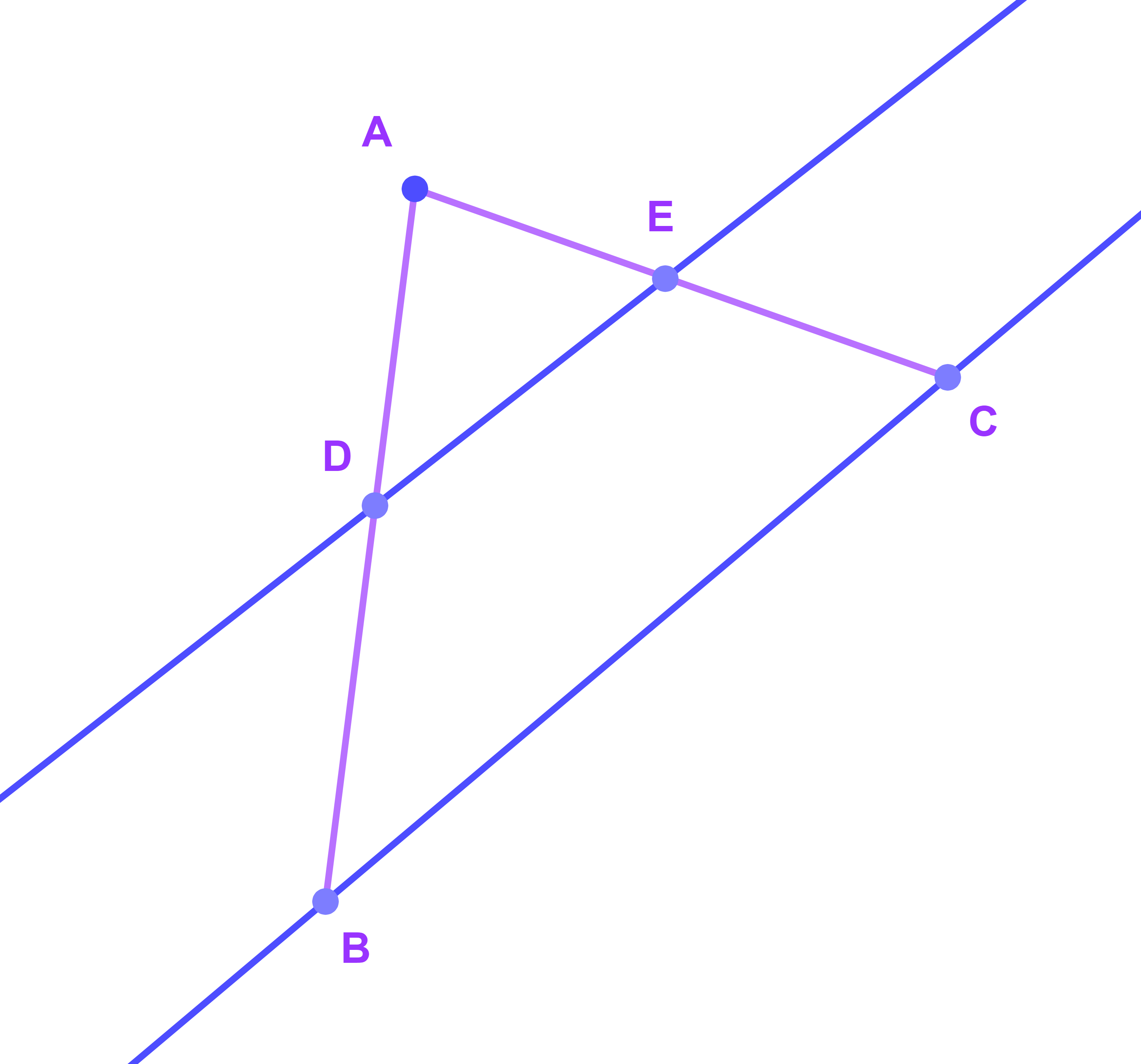
ليكن ABC مثلثا بحيث
AB=25; AD=12; AE=14 et AC=30 et E∈[AC] et F∈[AB]
هل (DE)||(BC) ?
تصحيح
نفترض ان المستقيمين متوازيان
(DE)||(BC) .
: حسب مبرهنة طاليس ان
| AB | = | AC |
| AD | AE | |
| 25 | = | 30 |
| 12 | 14 |
اي 350=360 وهذا غير ممكن,
نستنتج اذن ان المستقيمين (DE) و (BC)غير متوازيين
تمرين 7 tp
بين ان ∀n∈IN; a∈IR+: (1+a)n≥1+na
تصحيح
نبين بالترجع ان الخاصية ∀n∈IN;
a∈IR+: (1+a)n≥1+na صحيحة
توجد ثلاث مراحل للاجابة عن هذا السؤال
أ) نتحقق من الخاصية من اجل n=0 لان n يبدأ من الصفر (∀n∈IN)
(1+a)0=1 لان
1+a≠0 اذن
(1+a)0=1=1+0.a وهذا يعني ان الخاصية صحيحة من اجل n=0
ب) نفترض ان الخاصية صحيحة من اجل n ونبين انها صحيحة من اجل n+1
يعني نبين ان (1+a)n+1≥1+(n+1)a
ماذا يعني هذا؟ يعني نعتبر وضعية صحيحة في مرحلة ما ونبرهن اذا كانت صحيحة في المرحلة الموالية
لدينا اذن (1+a)n+1=(1+a).(1+a)n
وحسب الافتراض (1+a)n≥1+na
اذا ضربنا طرفي المتفاوتة بعدد موجب طرفا طرفا , المتفاوتة لا تتغير اذن
(1+a).(1+a)n≥(1+a)(1+na)
⇔(1+a)n+1≥1+na+a+na²
⇔(1+a)n+1≥1+a(n+1)+na²
na²> 0 اذن
1+a(n+1)+na²> 1+(n+1)a ومنه فان
(1+a)n+1≥1+a(n+1)
وهذا يعني ان الخاصية صحيحة من اجل n+1
ج) نستنتج اذن ان ∀n∈IN;
a∈IR+: (1+a)n≥1+na صحيحة