Produit vectoriel (1)
1- Orientation de l’espace - Produit vectoriel
1.1 Orientation de l’espace
1.1.1 Introduction
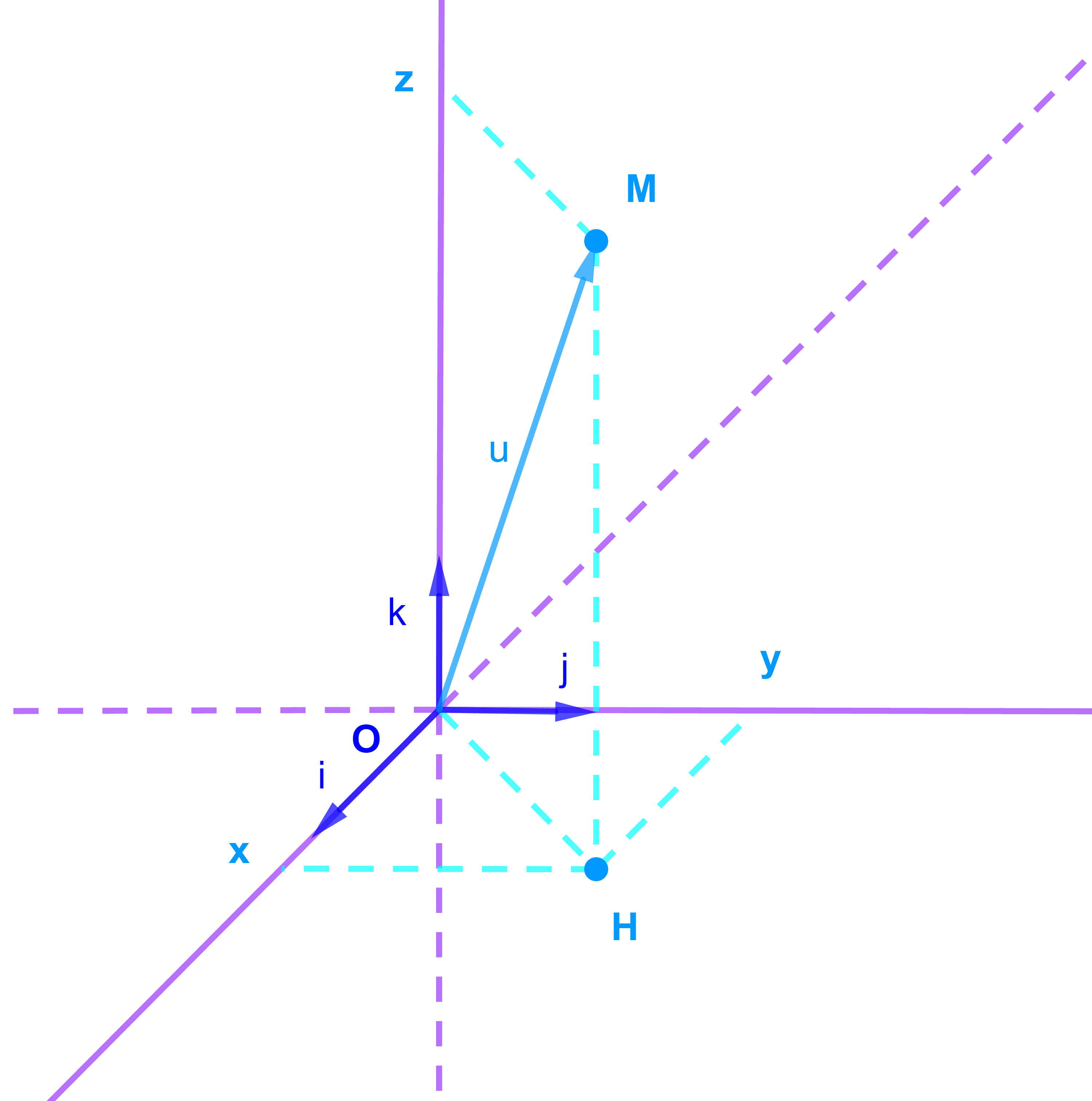
Soient i→ et j→ deux vecteurs orthogonaux de norme 1 dans l'espace usuel E3. Il y'a deux possibilités de leur adjoindre un troisième vecteur pour obtenir une base orthonormée dans V3, il existe donc deux bases B(i→;j→;k→) et B'(i→;j→;-k→).
1.1.2 Définition
Soit (OIJK) un tétraèdre.
On pose OI→=i→; OJ→=j→
et OK→=k→
Si l'angle (i→;j→) est positif
alors la base B(i→;j→;k→) est directe.
Et chaque triplet de vecteurs
non coplanaires (u→;v→;w→)
est orienté et l'espace est donc orienté.
1.1.3 Propriété
Soient B=(i→;j→;k→) une base orthonormée directe et O un point dans l'espace.
Le quadruplet (O;i→;j→;k→)
est un repère orthonormé direct.
Exemples
Soit (O;i→;j→;k→)
un repère orthonormé direct.
(i→;j→;k→)
est une base orthonormée directe.
(j→;i→;k→)
est une base orthonormée indirecte.
(j→;k→;i→)
est une base orthonormée directe.
1.2 Produit vectoriel
1.2.1 Définition
Soient u→ et v→ deux vecteurs
de V3.
Le produit vectoriel de u→
et v→, noté u→∧v→ est un vecteur défini par
1) Si u→ et v→ sont colinéaires alors
u→∧v→=O→.
2) Si u→ et v→
ne sont pas colinéaires alors
(a) (u→ ∧ v→)⊥u→
et (u→∧v→)⊥v→.
(b) La base (u→;v→;u→∧v→) est directe.
(c) ||u→∧v→||
=||u→||×||v→||sin(u→;v→).
1.2.2 Résultat
Soit S la surface d'un triangle (ABC).
| S = | 1 | ||AB→∧AC→|| |
| 2 |
| = | 1 | AB×ACsin(AB→;AC→) |
| 2 |
Exemples
| i→∧j→=k→ | k→∧j→ = - i→ | k→∧i→ = j→ | i→∧i→=O→ | j→∧j→ = O→ | k→∧k→ = O→ |
1.2.3 Antisymétrie et Bilinéarité
Soient u→ ; v→ et w→
des vecteurs dans V3 et k un nombre réel non nul.
Antisymétrie
u→∧v→=- v→∧u→
Bilinéarité
u→∧(v→+w→)=u→ ∧ v→ + u→ ∧ w→
et ku→∧v→ = u→∧(kv→) = (ku→)∧v→
Remarque
L'associativitée n'est pas vérifiée en général
c'est à dire u→∧(v→∧w→)≠(u→∧v→)∧w→.