تمرين 4 tp

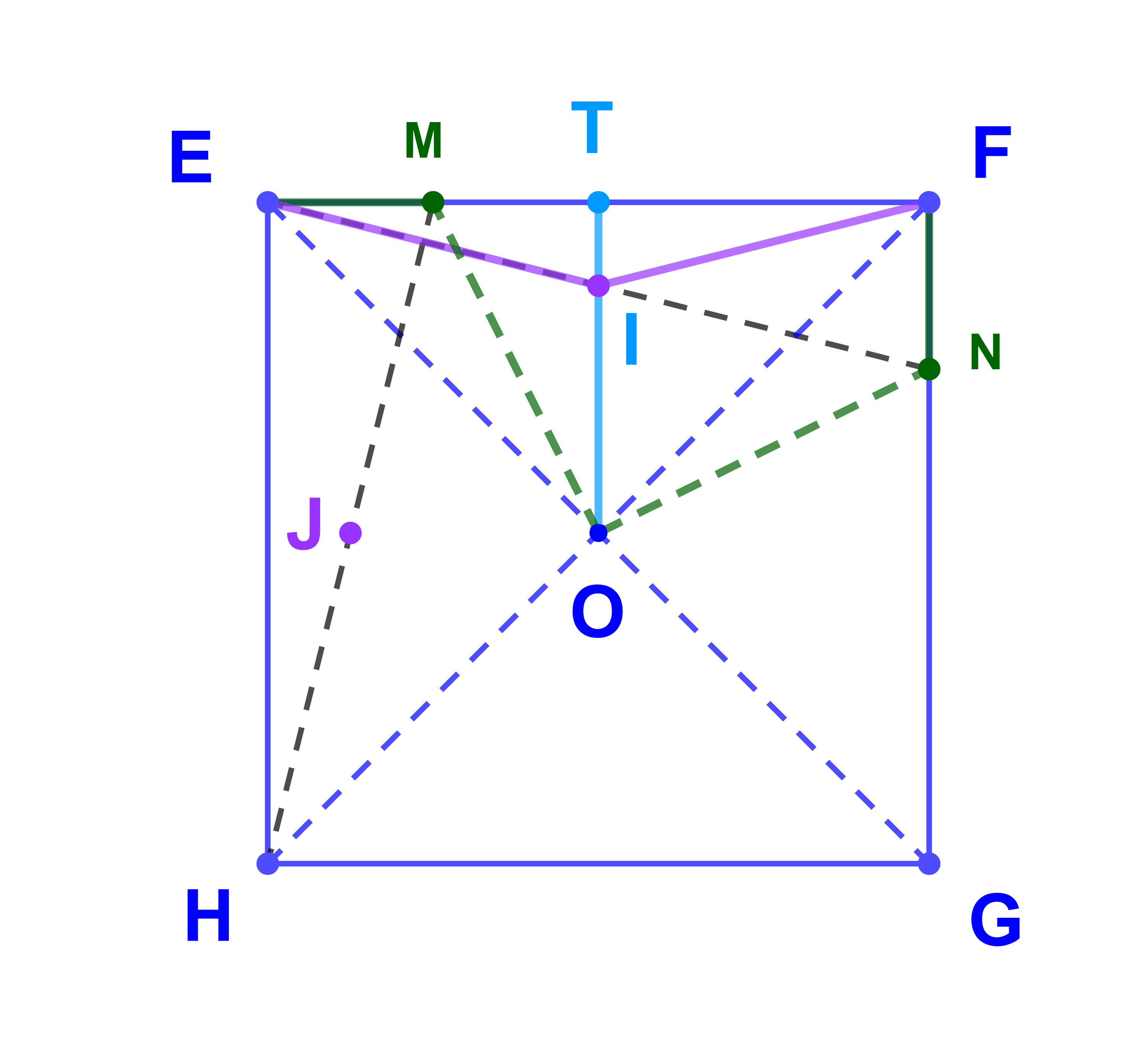
ليكن EFGH مربعا مركزه O و N∈[FG] بحيث FN^→=xFG^→ و M∈[EF] بحيث EM^→=xEF^→ و x∈IR
1) انشئ الشكل
2) حدد مركز وزاوية الدوران r الذي يحول F الى E ويحول G الى F
3) بين ان r(N)=M
4) لتكن I منتصف القطعة [EN]
(q1) بين ان المثلث IEF متساوي الساقين
(q2) حدد r(I)
5) حدد المحل الهندسي للنقطة I عندما تتغير M على [EF]

تصحيح

1) الشكل

2) r(F)=E⇒Ω∈med(EF)
r(G)=F⇒Ω∈med(FG)
اذن G∈med(EF)∩med(FG)
وبما ان EFGH مربع فان
med(EF)∩med(FG)={O} اذن O مركز الدوران r ونعلم ان قطري مربع متعامدان
اذن

(OF;OE)≡	π	[2π]
	2

وبالتالي r دورانا مركزه O وزاويته

α≡	π	[2π]
	2

3) نبين ان r(N)=M نضع r(N)=N'
لدينا FN^→=xFG^→ ونعلم ان الدوران يحافظ على معامل استقامية متجهتين وبما ان r(F)=E و r(G)=F فان EN'^→=xEF^→
ولدينا EM^→=xEF^→ اذن EN'^→ =EM^→
وهذا يعني ان N'=M وبالتالي r(N)=M

4) (q1) نعتبر المثلث EGN , لدينا O منتصف القطر [EG] و I منتصف [EN] اذن (OI)||(GN) وبما ان EFGH مربع فان (OI) واسط القطعة [EF] اذن IE=IF وبالتالي المثلث IEF متساوي الساقين
(q2) نحدد r(I), لدينا OE=OH و(OE)⊥(OH) اذن r(E)=H ولدينا r(N)=M و I منتصف [EN] وبما ان الدوران يحافظ على منتصف قطعة فان r(I)=J حيث J منتصف [MH]

5) لدينا EM^→=xEF^→ اذن عندما تتغير M على القطعة [EF] فان x يتغير في المجال [0;1]

IO→ =	1	NG→ =	1	(NF→+FG→)
	2		2

=	(1-x)	FG→ = tFG→ ;	t∈[0;	1	]
	2			2

وهذا يعني ان المحل الهندسي ل I هو القطعة [OT]