Etude de fonctions (12)
Exercice 1 tp
Soit f une fonction numérique définie par
| { | f(x) = | 2x | si x≤0 |
| x²+1 | |||
| f(x) = | 2√(x) | si x> 0 | |
| x²+1 |
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) Déterminer D, le domaine de définition de f
2) Calculer les limites suivantes
lim (-1) |
f(x) | ; | lim 1+ |
f(x) |
lim -∞ |
f(x) | et | lim +∞ | f(x) |
et déterminer les asymptotes de (C).
3) Etudier la continuité et la dérivabilité de f au point 0.
4) Etudier la monotonie de f sur les intervalles ]-∞;0[ ; ]0;+∞[
et tracer son tableau de variations.
5) Tracer la courbe (C) et résoudre graphiquement et selon la paramétre m l'équation f(x)=m.
Correction
1)
D={x∈]-∞;0]/ f(x)∈IR}
∪{x∈]0;+∞[/ f(x)∈IR}
i1. (∀x∈]-∞;0]: x²+1≠0) ⇒f(x)∈IR
i2. (∀x∈]0;+∞[: √(x)∈IR et x²+1≠0) ⇒f(x)∈IR
⇒ D=]-∞;0]∪]0;+∞[=IR.
lim -∞ |
f(x) = | lim -∞ |
2x |
| x²+1 |
=lim -∞ |
2x | =lim -∞ |
2 |
| x² | x |
| donc | lim -∞ |
f(x) = 0 |
lim +∞ |
f(x) = | lim +∞ |
2√(x) |
| x²+1 | |||
| = | lim +∞ |
2x | |
| (x²+1)√(x) |
=lim +∞ |
2 | × | lim +∞ |
1 |
| x | √(x) |
lim +∞ | 2 | = 0 et | lim +∞ | 1 | = 0 |
| x | √(x) |
| donc | lim +∞ |
f(x) = 0 |
Asymptotes de (C)
| On a | lim -∞ | f(x) = 0 |
Donc (C) admet une asymptote d'équation y=0 au voisinage de -∞.
| on a | lim +∞ | f(x) = 0 |
donc (C) admet une asymptote d'équation y=0 au voisinage de +∞.
3) (a) Continuité au point 0, on a f(0)=0
lim 0- |
f(x) = | lim 0- | 2x |
| x²+1 |
| = | 2.0 | = 0 |
| 0²+1 |
| donc | lim 0- |
f(x) = 0 = f(0) |
ainsi f est continue à gauche à 0.
lim 0+ | f(x) = | lim 0+ | 2√(x) | = 0 |
| x²+1 |
| = | 2√(0) | = 0 |
| 0²+1 |
| Donc | lim 0+ |
f(x) = 0 = f(0) |
ainsi f est continue à droite à 0.
Puisque f est continue à droite et à gauche à 0
alors f est continue au point 0.
(b) Dérivabilité à gauche à 0
lim 0- | f(x)-f(0) | =lim 0- | 2 | = 2=f'g(0) |
| x-0 | x²+1 |
f est dérivable à gauche à 0.
Dérivabilité à droite à 0
lim 0+ |
f(x)-f(0) | =lim 0+ |
2 |
| x-0 | (x²+1)√(x) |
lim 0+ |
2 | = 2 | et | lim 0+ |
1 | = +∞ |
| (x²+1) | √(x) |
| donc | lim 0+ |
f(x)-f(0) | =+∞ |
| x-0 |
alors f n'est pas dérivable à droite à 0 et donc n'est pas dérivable en 0.
4) Monotonie de f sur ]-∞;0[
| f(x) = | 2x | si x≤0 |
| x²+1 |
x→2x et x→x²+1 sont dérivables sur IR et en particulier sur ]-∞;0[
et puisque (∀x∈]-∞;0[): x²+1≠0 alors f est dérivable sur I=]-∞;0[. Soit x∈I
| f '(x)= | 2(x²+1)-2x.2x | = | -2(x²-1) |
| (x²+1)² | (x²+1)² |
f'(x) est de signe de -2(x²-1).
f'(x)=0⇔x=1 ou x=-1.
On a x≤0 donc x=-1
a=-2< 0 (fonction de référence) alors
| { | f '(x) ≥ 0 | si x∈[-1;0] |
| f '(x) ≤ 0 | si x∈]-∞;-1] |
f est donc strictement décroissante sur
]-∞;-1] et strictement croissante sur [-1;0].
Monotonie de f sur ]0;+∞[.
x→2√x et x→x²+1 sont dérivables sur ]0;∞[
et puisque ∀x∈]-∞;0] on a x²+1≠0 alors f est dérivable sur ]0;+∞[.
| f(x) = | 2√(x) | si x> 0 |
| x²+1 |
| f '(x) = | (x²+1)÷(√x)-4x.√x | = | -(3x²-1) |
| (x²+1)² | (x²+1)²√(x) |
f'(x) est de signe de -(3x²-1).
f'(x)=0⇔x=√(1/3) ou x=-√(1/3).
x > 0 donc x=√(1/3)
a=-3< 0 (fonction de référence)
| { | f '(x) ≥ 0 | si x∈]0 ; √(1/3)] |
| f '(x) ≤ 0 | si x∈[√(1/3) ; +∞[ |
alors f est strictement croissante sur
]0;√(1/3)] et strictement décroissante sur [√(1/3);+∞[.
| { | f '(x) = | -2(x²-1) | si x≤0 |
| (x²+1)² | |||
| f '(x) = | - (3x²-1) | si x> 0 | |
| (x²+1)√(x) |
Tableau de variations de f
| x | -∞ | -1 | 0 | √(1/3) | +∞ | ||||
| f'(x) | - | 0 | + | 2|| | + | 0 | - | ||
| f | 0 | ↘ | -1 |
↗ |
0 | ↗ | √(3√(3))/4 | ↘ | 0 |
5) La courbe
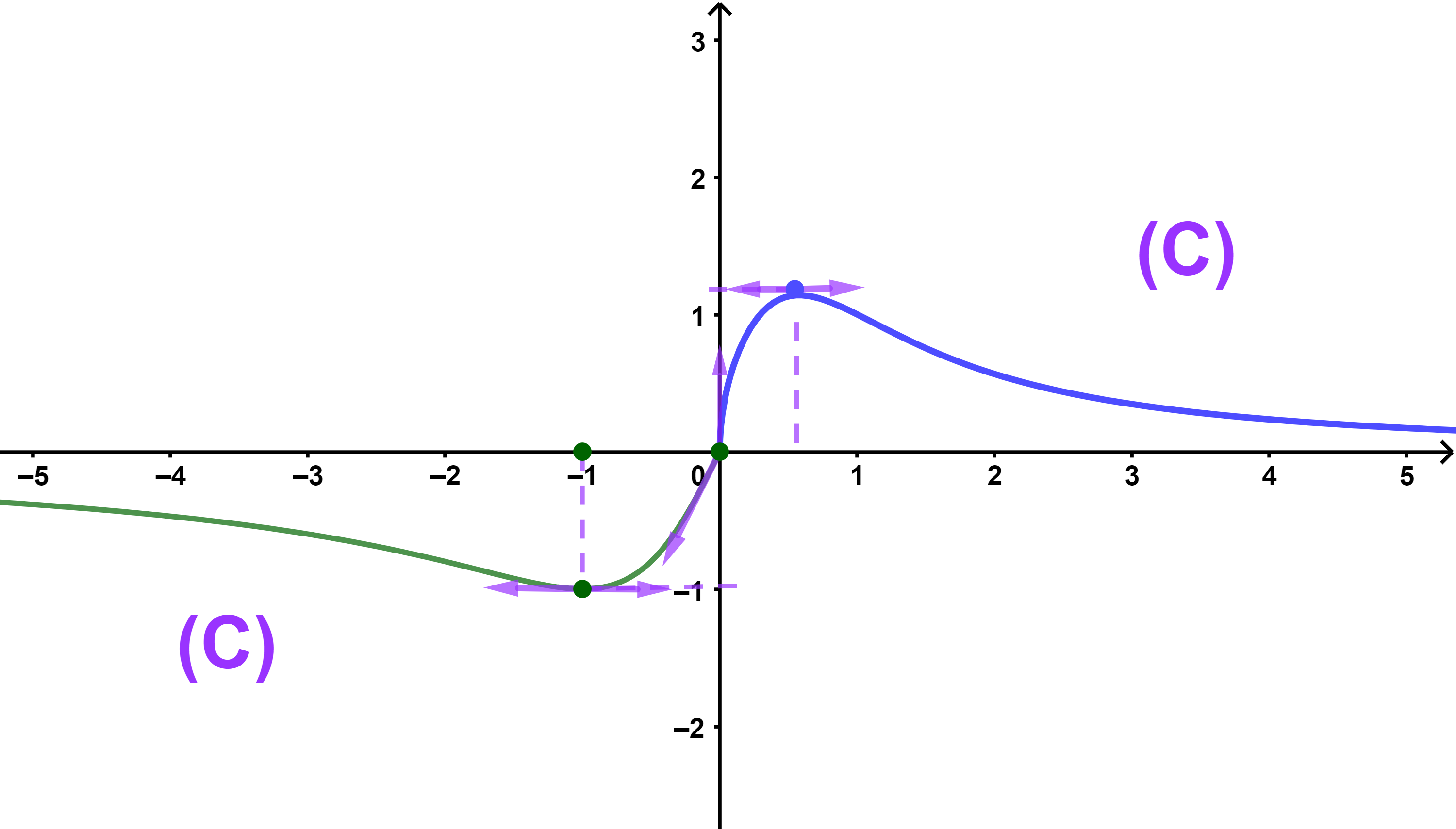
Pour résoudre graphiquement l'équation (E): f(x)=m on considère les droites parallèles à l'axe des ordonnées, notée (Dm).
Si m<-1 ou m> f(√(1/3)) alors (Dm) ne coupe pas la courbe et donc l'équation (E) n'a pas de solution.
Si m=-1 alors (Dm) coupe la courbe en un seul point et donc l'équation (E) admet une seule solution -1.
Si (-1< m < 0) ou (0< m < f(√(1/3)) alors (Dm) coupe la courbe en deux points et donc l'équation(E) admet deux solutions.
Si m=0 ou m=f(√(1/3)) alors (Dm) coupe la courbe en un seul point et donc l'équation (E) admet une seule solution.