Calcul Intégral (1)
Intégrale d’une fonction
1- Intégrale d’une fonction continue sur un segment
1.1 Définition et notations
Soient f une fonction définie sur I=[a;b] et F une primitive de f.
Le nombre F(b)-F(a) est appelé intégrale de la fonction f de a à b et on écrit
| b ∫ a |
f(x)dx | = [F(x)] | b a |
On lit somme f(x)dx de a à b ou intégrale de a à b de f(x)dx.
Remarque
1) Si G est une autre primitive de f alors
| b ∫ a |
f(x)dx | = [G(x)] | b a |
= G(b)-G(a)=F(b)-F(a).
2) On peut utiliser autre lettre que x, par exemples t;u;..
| b ∫ a |
f(x)dx | = | b ∫ a |
f(t)dt | = [F(t)] | b a |
Exemple 1
| 2 ∫ 1 |
3x²dx | = [x³] | 2 1 |
= 8-1=7 |
Exemple 2
| e ∫( 2 |
1 | )dx = [lnx] | e 2 |
= lne -ln2= 1-ln2 |
| x |
1.1.2 Interprétation géométrique de l'integrale
Le plan est rapporté à un repère orthonormé (O;i→;j→). On considère une fonction f continue et positive sur un intervalle [a ; b] et (C) sa courbr représentative. L'intégrale I définie par
| I = | b ∫ a |
f(x)dx |
représente S, l'aire du domaine délimité par la courbe (C) ; l'axe des abscisses et les deux droites (D):x=a et (D'):x=b.
Démonstration
On subdivise le segment [a;b] en n subdivisions de largeur
| δ= | b-a |
| n |
On considère les micros rectangles de largeur δ et de hauteur f(xi).
L'aire de chaque rectangle est égal à δ.f(xi).
Il y'a deux façons différentes de tracer ces rectangles.
Nous étudierons une seule façons, le cas d'une fonction croissante sur l'intervalle I et nous reviendrons sur ce paragraphe à la fin de ce tutoriel.
Première façon un des sommets de chaque rectangle est sous la courbe (C) et les deux sommets qui appartiennent à l'axe des abscisses
alors la somme de leurs surfaces est notée un.
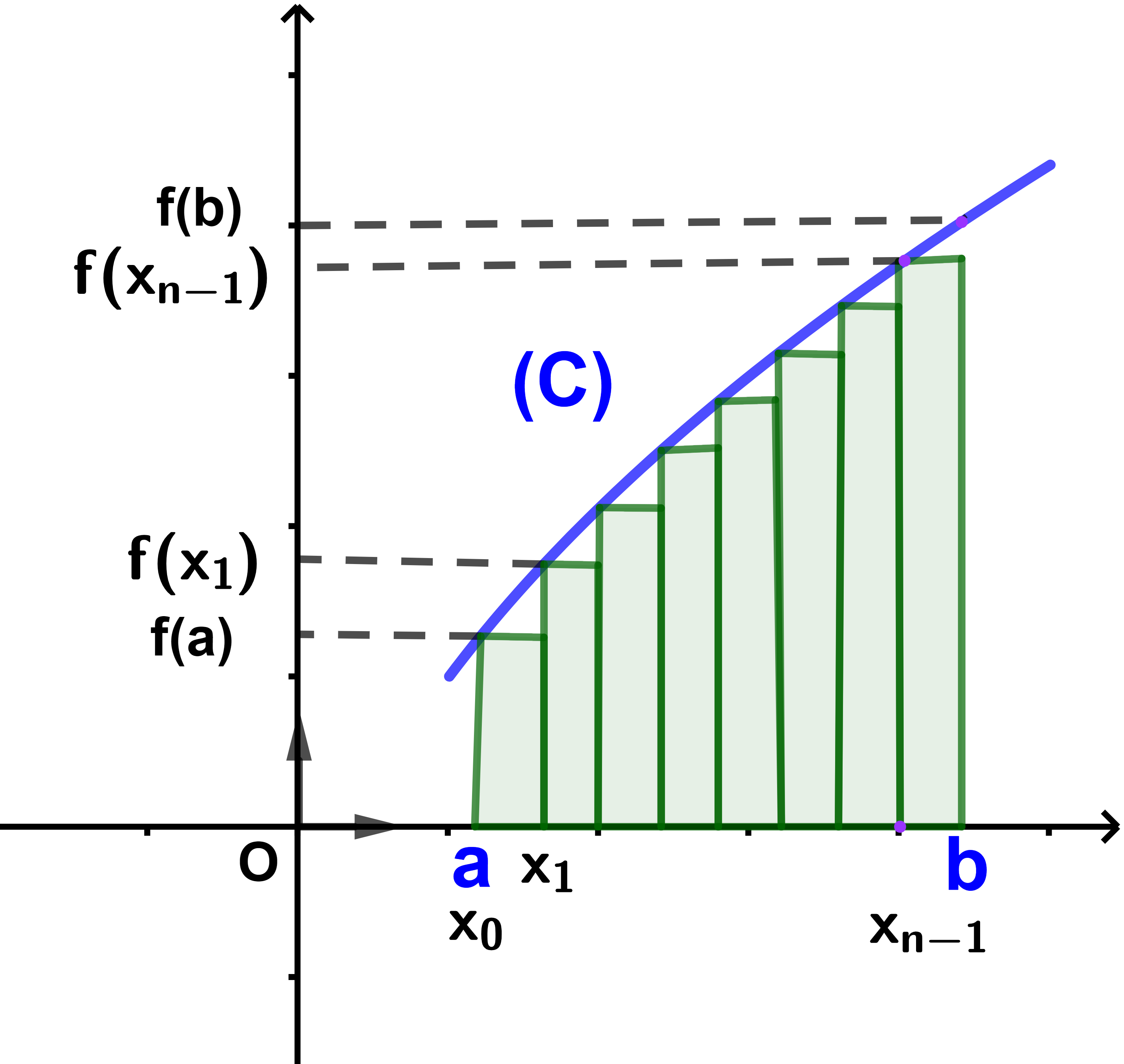
un=δ.f(x0) + δ.f(x2) + .. + δ.f(xn-1)
| un = δ . | k=n-1 Σ k=0 |
f(a+kδ) |
un est une approximation par défaut du surface S donc
| un ≤ | b ∫ a |
f(x)dx |
et quand n→+∞ alors la suite (un) tend vers S.