Calcul de probabilités (9)
3.4 Fonction de répartition
3.4.1 Définition
Soient (w;p) univers probabilisé fini et x la variable aléatoire définie sur w
et x(w)={x1 ; x2 ;..; xq}.
On appelle Fonction de répartition la fonction F définie de IR vers [0;1] par F(x)=p(X < x)
∀x∈]xi ; xi+1]
F(x) = p(X = x1)+p(X = x2) +..+ p(X = xi).
Pourquoi p(X = xi) et pas p(X = xi+1 alors tout simplement
X< x et xi+1∈]xi ; xi+1]
| x | F(x) = p(X < x) |
|---|---|
| ]-∞ ; x1] | 0 |
| ]x1 ; x2] | p(X = x1) |
| ]x2 ; x3] | p(X = x1+p)(X = x2) |
| .. | .. |
| ]xn-1 ; xn] | p(X = x1)+p(X = x2) +..+ p(X = xn-1) |
| ]xn ; +∞[ | 1 |
3.4.2 Exemple
Soient (w ; p) univers probabilisé fini et x la variable aléatoire définie sur w.
On considère la loi de probabilité finie de x définie par le tableau suivant
| xi | 0 | 1 | 2 | 3 |
| p(X=xi) | 0,3 | 0,4 | 0,1 | 0,2 |
Déterminons la fonction de répartition de la variable x.
| x | F(x) = p(X< x) | |
|---|---|---|
| ]-∞ ; 0] | 0 | |
| ]0 ; 1] | p(X=0)=0,3 | |
| ]1 ; 2] | p(X=0)+p(X=1)=0,7 | |
| ]2 ; 3] | p(X=0)+p(X=1)+p(X=2)=0,8 | |
| ]3 ; +∞[ | 1 |
Exercice 1 tp
Le tableau ci-dessous détermine la loi de probabilité d'une variable aleatoire X
| xi | 0 | 1 | 2 | 3 | 4 | |
| p(X=xi) | 0,2 | 0,1 | 0,4 | 0,2 | 0,1 |
1) Déterminer F la fonction de la répartition de la variable aléatoire X.
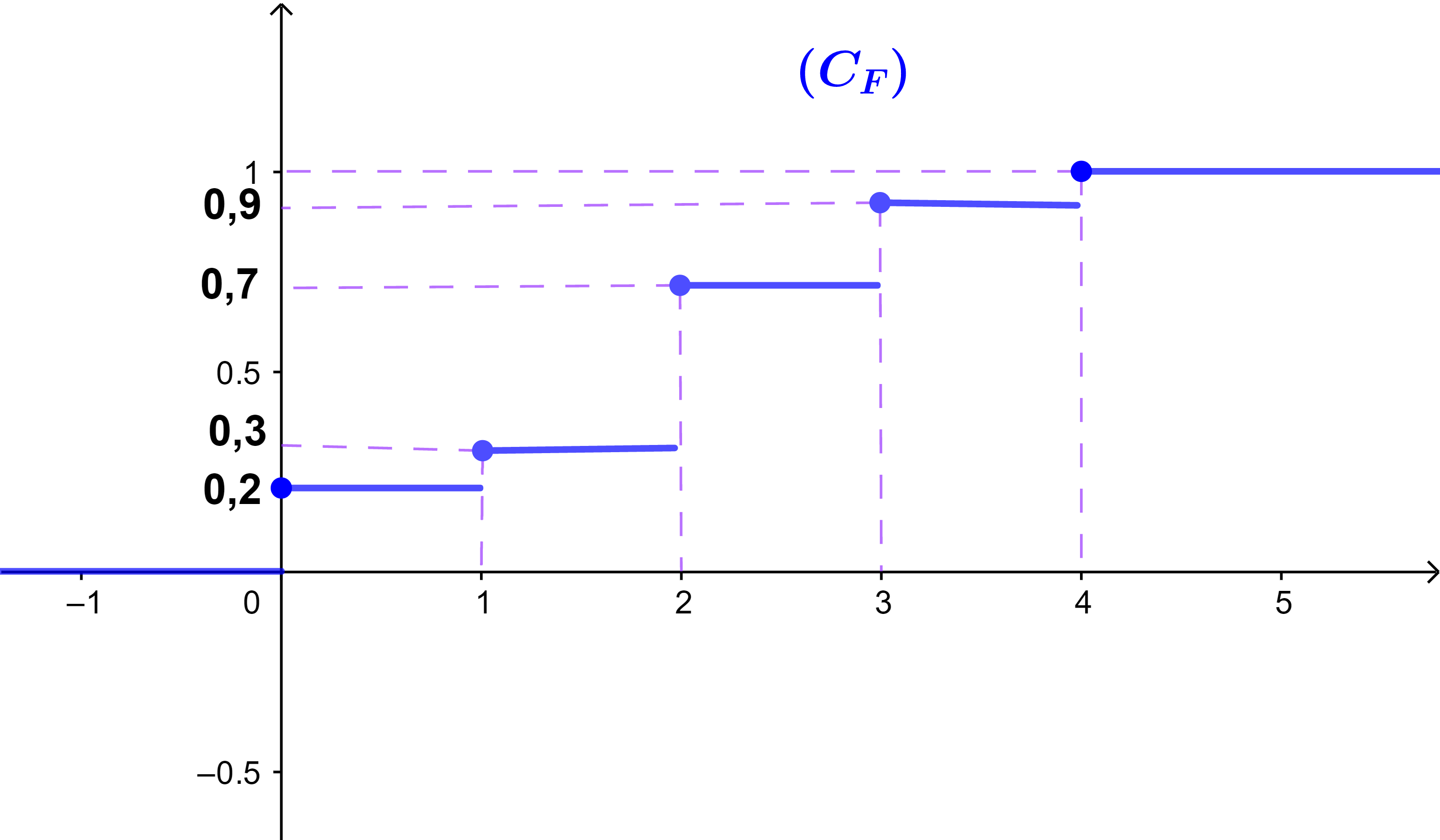
2) Tracer dans un repère orthogonal la courbe représentative de la fonction de répartition F.
Correction
1) On rappelle que F est définie de IR vers [0;1] par
X(Ω)={0 ; 1 ; 2 ; 3 ; 4}.
| (x∈IR) | F(x) = p(X < x) |
| Si x∈]-∞ ; 0] | F(x) = 0 |
| Si x∈]0 ; 1] | F(x) = p(X=0) = 0,2 |
| Si x∈]1 ; 2] | F(x) = p(X=0)+p(X=1) = 0,3 |
| Si x∈]2 ; 3] | F(x) = p(X=0) +p(X=1) +pX=2) = 0,7 |
| Si x∈]3 ; 4] | F(x) = p(X=0) + p(X=1) +p(X=2)+p(X=3) = 0,9 |
| Si x∈]4 ; +∞[ | F(x) = 1 |
2) la courbe représentative (CF)