Vecteurs de l'espace (4)
2.3.3 Exemples
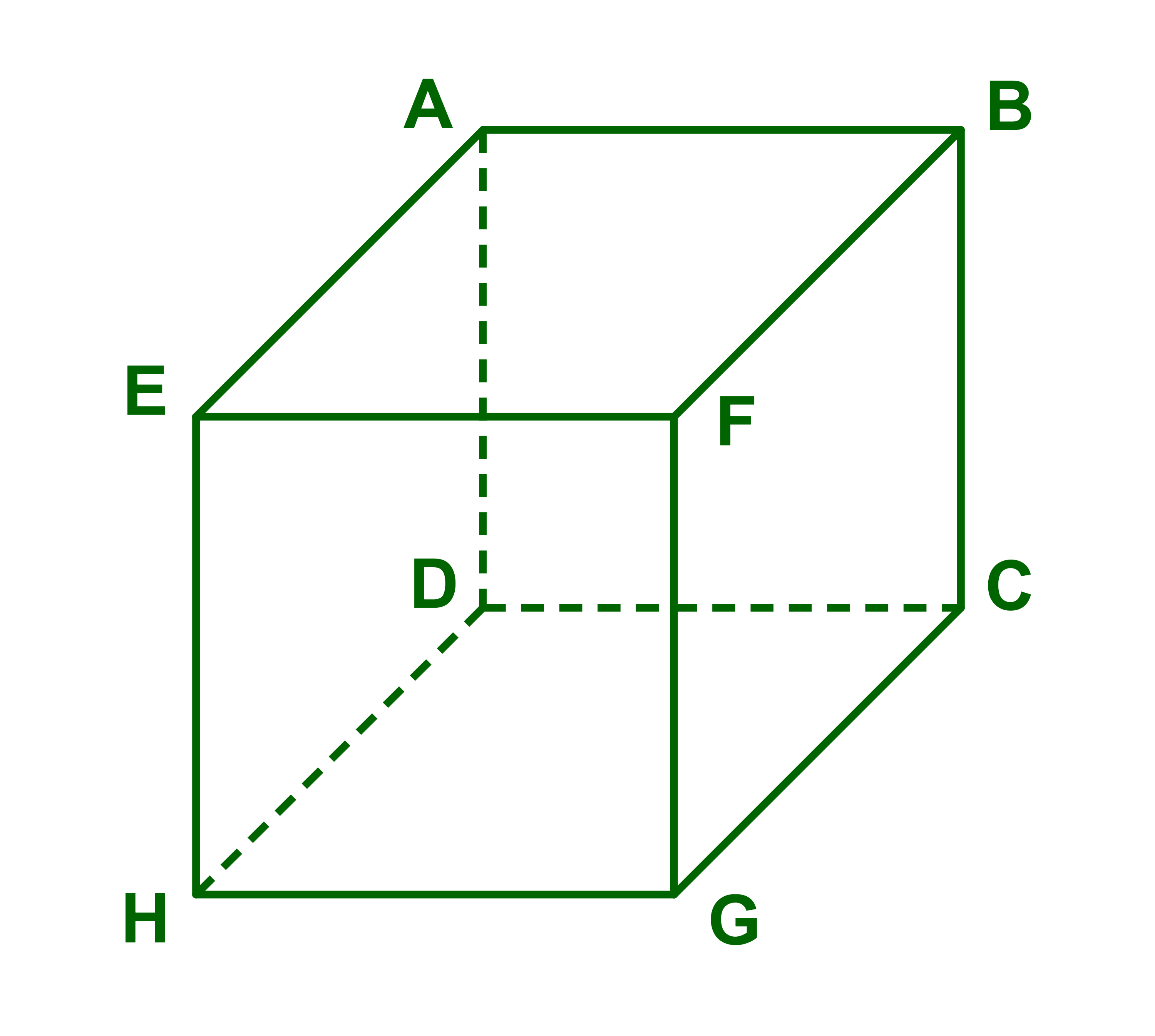
1) Soit ABCDEFGH un cube.
Les points A ; B ; C et D sont coplanaires.
Les vecteurs AB→ ; AC→ et AD→ sont donc coplanaires.
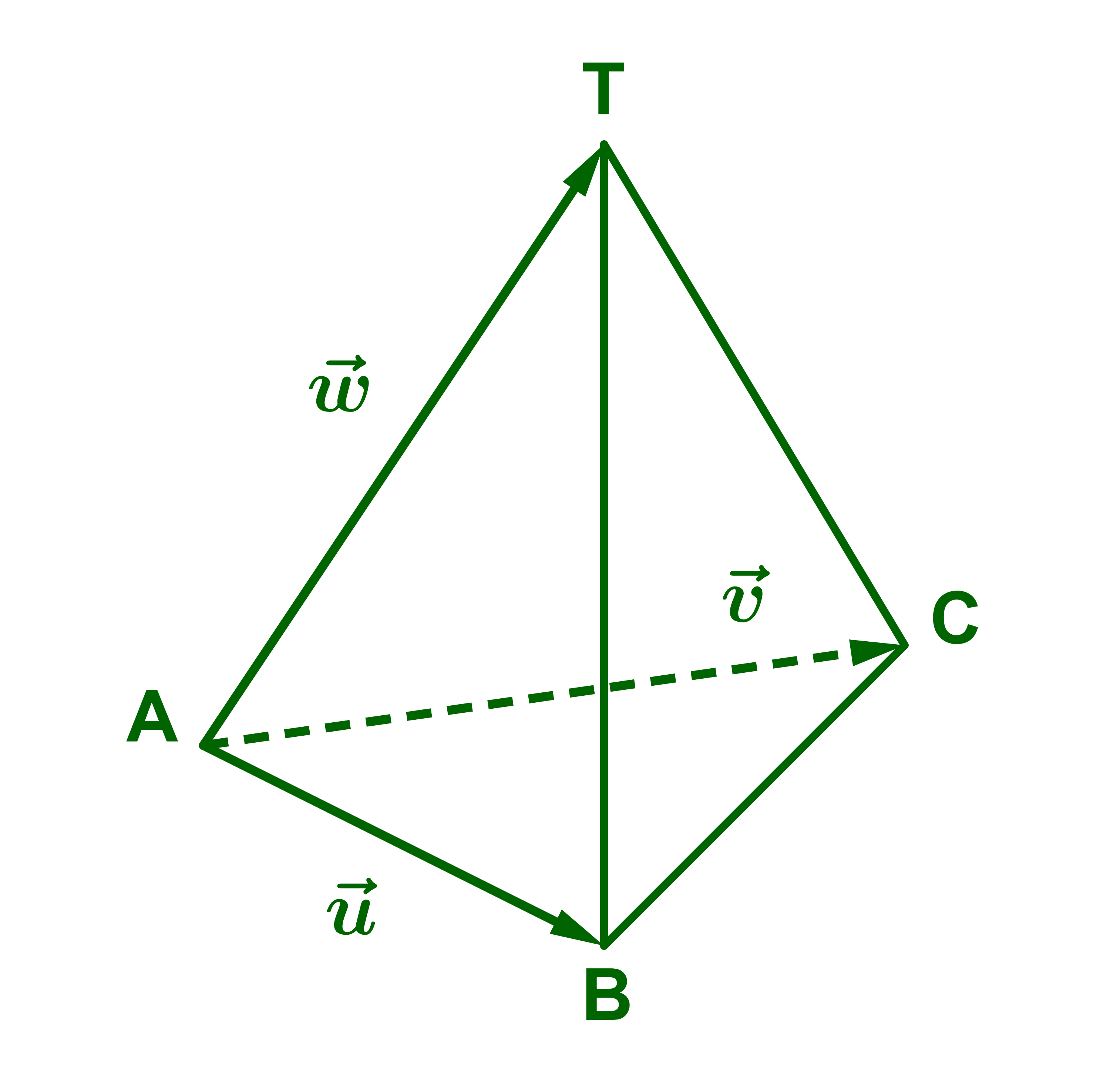
2) Si TABC est un tétraèdre alors les points A ; B ; C et T ne sont pas coplanaires
ainsi les vecteurs AB→ ; AC→ et AT→ ne sont pas coplanaires.
2.3.4 Propriété
Soient u→ et v→ deux vecteurs non colinéaires
et w→∈𝕍3.
u→ ; v→ et w→ sont coplanaires ⇔
(∃(x;y)∈IR²): w→=xu→+yv→.
2.3.5 Résultat
Si (∃(x;y)∈IR²): AM→=xAB→+yAC→ alors A ; B ; C et M sont coplanaires.