تمرين 1 tp

ليكن TBCD رباعي اوجه, بحيث كل اوجهه مثلثات متساوية الاضلاع
بين ان TC^→ ⊥BD^→ ; TB^→⊥CD^→ و TB^→⊥CD^→.

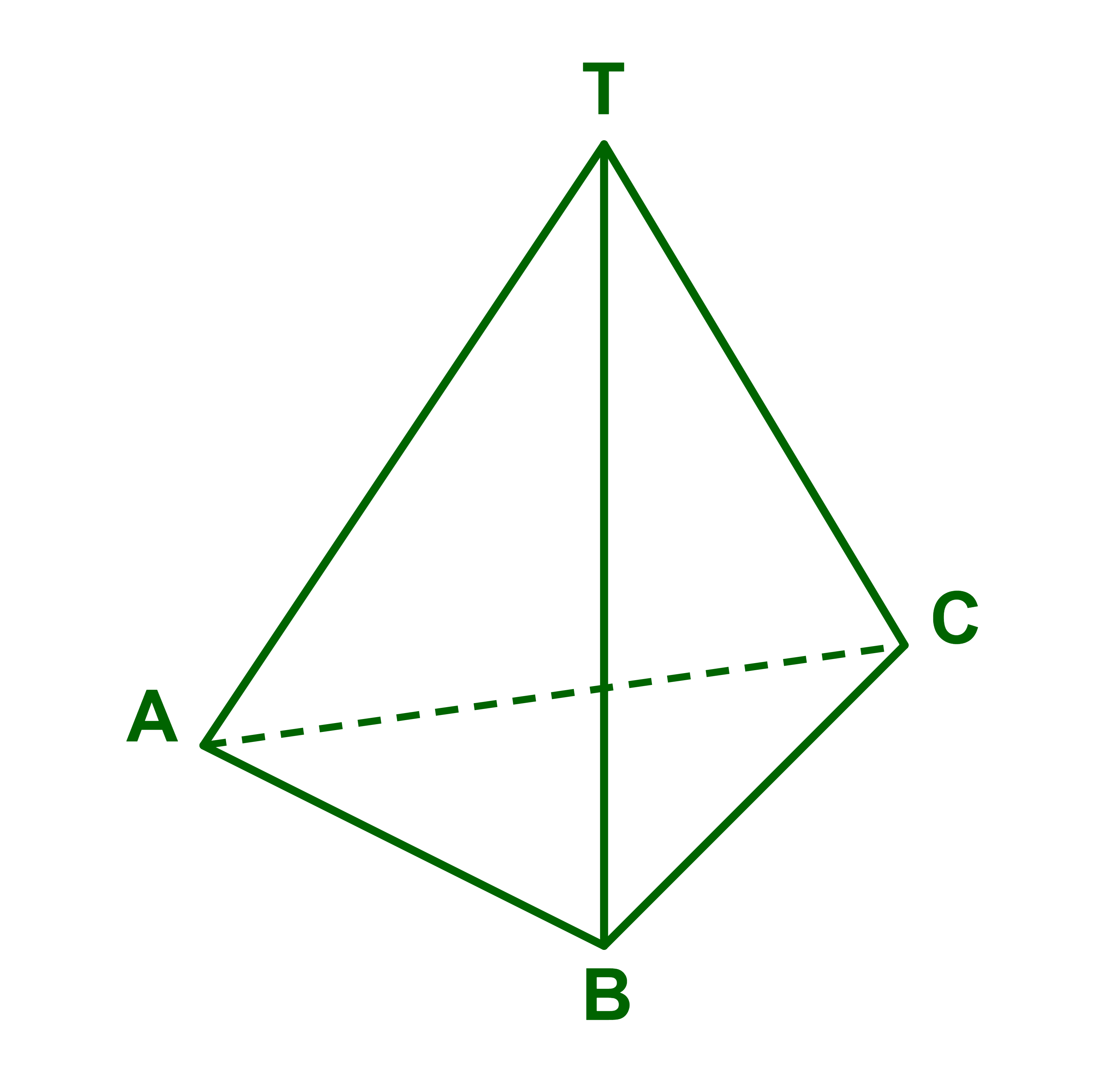
تصحيح

1) نبين ان TC^→ ⊥BD^→
نعتبر المثلث المتساوي الاضلاع TBD و I منتصف القطعة [BD]
لدينا (BD)⊥(TI)
نعتبر المثلث المتساوي الاضلاع CBD
لدينا (BD)⊥(CI)
اذن

{	(BD)⊥(TI)	⇒ (BD)⊥(TCI)
	(BD)⊥(CI)

لدينا اذن

{	(TC)⊂(TCI)	⇒ (BD)⊥(TC)
	(BD)⊥(TCI)

ومنه فان TC^→ ⊥BD^→

نبين بنفس الطريقة
TB^→⊥CD^→ و TB^→⊥CD^→

تمرين 2 tp

ليكن TBCD رباعي اوجه, O منتصف القطعة [BD] و I و J نقطتين بحيث

BI→ =	1	BC→	;	DJ→ =	1	DC→
	3				3

1) بين ان I; J; T و D غير مستوائية
2) لتكن K نقطة بحيث

CK→ =	2	CO→
	3

بين ان K منتصف القطعة [IJ]

تصحيح

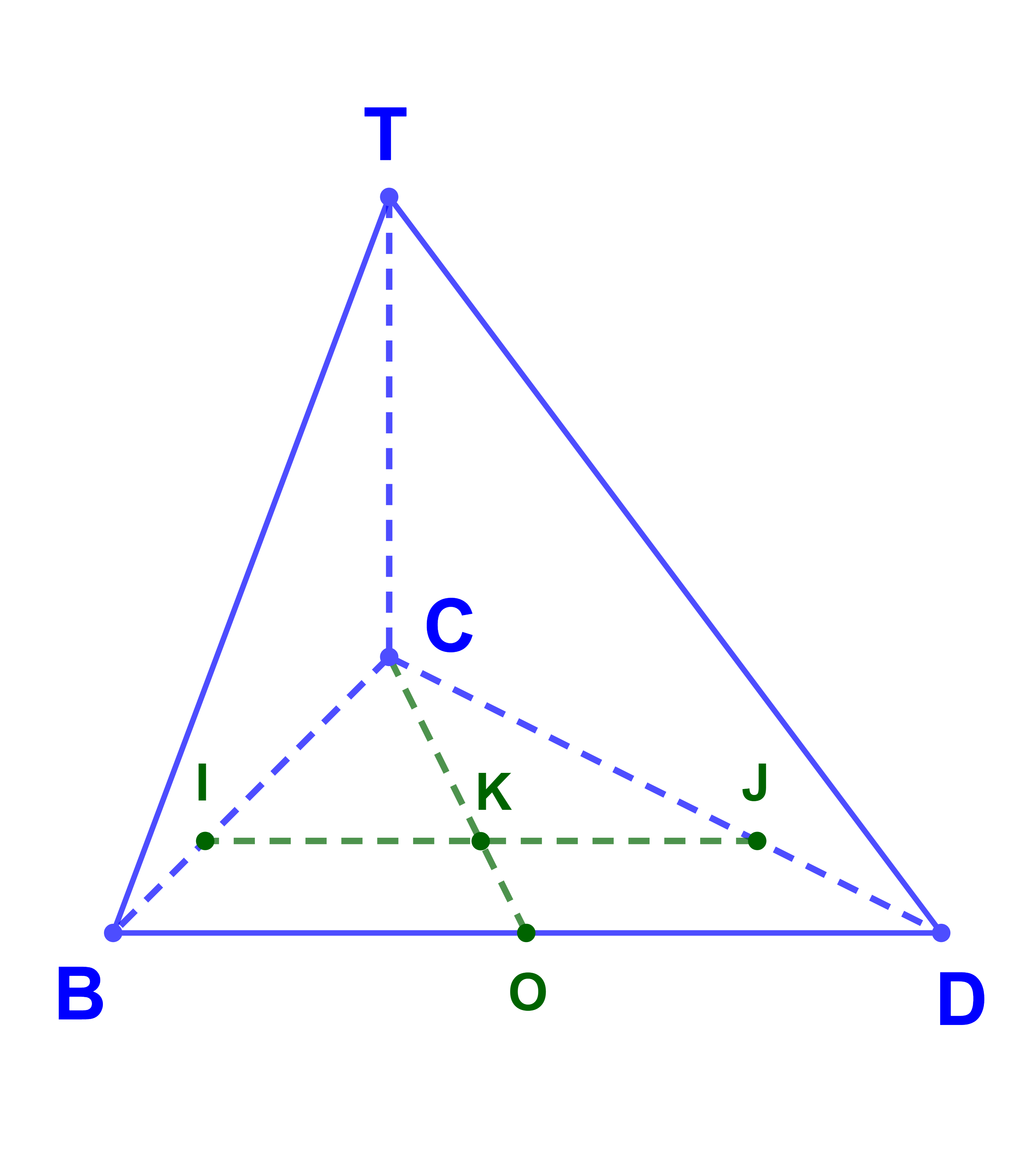1) نبين ان I; J; T و D غير مستوائية
نفترض انها مستوائية اذن توجد في نفس المستوى , المستوى (IJD) لان النقط I; J و D غير مستوائية
ومنه فان T∈(IJD)

اذن (TCD); (TBD) و (BCD) مستويات منطبقة وهذا يتنافى مع كون (TBDC) رباعي اوجه وبالتالي النقط I; J; T و D غير مستوائية
2) نبين ان K منتصف [IJ]

CK→ =	2	CO→	⇒ OK→ =	1	OC→
	3			3

لدينا من جهة اولى

{	OK→ =	1	OC→
		3
	BI→ =	1	BC→
		3
⇒	KI→ =	1	OB→
		3

ومن جهة اخرى

{	OK→ =	1	OC→
		3
	DI→ =	1	DC→
		3
⇒	KJ→ =	1	OD→
		3

وبما ان O منتصف [BD] فان OD^→= - OB^→ اذن

KJ→ =	-1	OB→= -KI→
	3

KI^→ = - KJ^→ يعني ان I, منتصف القطعة [IJ]

تمرين 3 tp

ليكن TBCD رباعي اوجه و I و J نقطتين بحيث

DI→ =	1	TB→	;	BJ→ =	1	BT→	+ BC→
	2				2

1) انشئ الشكل
2) بين ان النقط I; D; J و C مستوائية
3) بين ان الرباعي IDJC متوازي اضلاع

تمرين 4 tp

ليكن PABCD هرما قاعدته, ABCD مربع مرطزه O وكل الاوجه الاخرى مثلثات متساوية الاضلاع
لتكن M نقطة من المستوى (ABC) بحيث

OM→ =	1	AB→
	2

1) حدد المحل الهندسي للنقطة M
2) لتكن N منتصف [PM]
عندما M تتغير في المستوى (ABC), حدد المحل الهندسي للنقطة N مع تحديد عناصره المميزة