Espace analytique (1)
2- Repère dans l'espace
2.1 Coordonnées d’un point et d'un vecteur
2.1.1 Définition
Soient O un point dans l'espace 𝔼 et i→ ; j→ et k→ trois vecteurs non coplanaires.
Le quadruplé (O;i→;j→;k→)
est appelé repère dans l'espace.
Si de plus i→ ; j→ et k→
sont orthogonaux deux à deux
et ||i→||=||j→||=||k→||=1
alors le repère est orthonormé.
Notons que désormai l'espace 𝔼 est rapporté au repère orthonormé (O;i→;j→;k→).
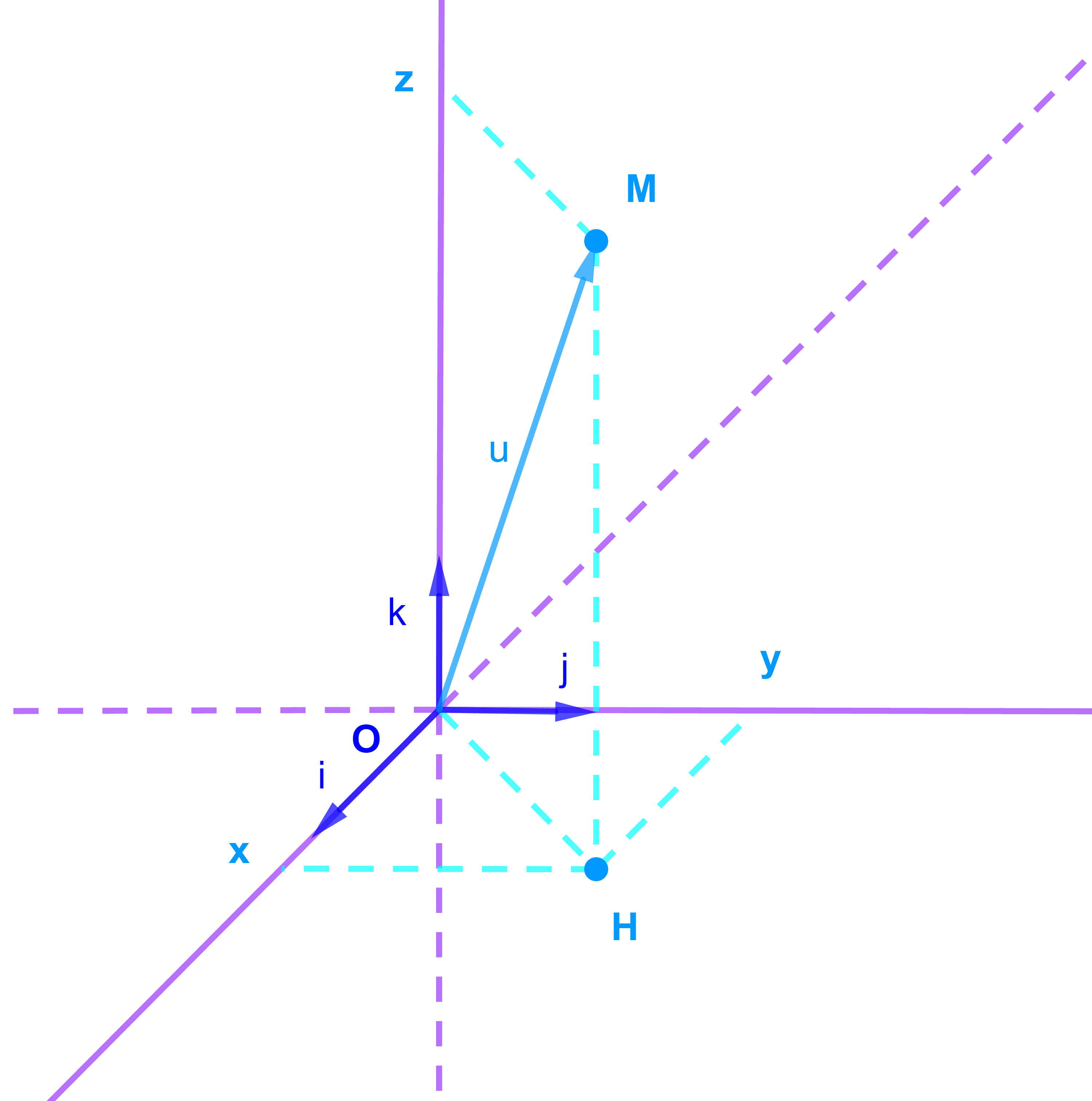
2.1.2 Coordonnées d’un point
L'espace 𝔼 est rapporté à un repère orthonormé (O;i→;j→;k→).
(∀M∈𝔼)(∃(x;y;z)∈ℝ³):
OM→= xi→+yj→+zk→.
Les nombres x ; y et z sont appelés les coordonnées du points M et on écrit M(x;y;z).
On dit également que les nombres x ; y et z sont les coordonnées du vecteur OM→ et on écrit OM→(x;y;z) Ou encore
| OM→ | x | |
|---|---|---|
| y | ||
| z |
x est l'abscisse de M.
y est l'ordonnée de M.
z est le cote de M.
2.1.3 Coordonnées d’un vecteur dans une base
Base de l'espace Trois vecteurs u→ ; v→ et w→ non coplanaires déterminent une base dans l'espace, noté (u→;v→;w→).
Exemple (O;i→;j→;k→) est un repère de l'espace donc (i→;j→;k→) est une base.
Propriété
Soit B=(u→;v→;w→) une base.
(∀e→∈𝕍3)(∃(x;y;z)∈IR³)
e→=xu→+yv→+zw→
et on écrit e→B(x;y;z).
Coordonnées de u→+v→
Soit (i→;j→;k→) une base de l'espace.
On considère deux vecteurs u→(x;y;z) et v→(x';y';z').
On a u→+v→(x+x';y+y';z+z').
Exemple
Soient u→(3;1;2) et v→(-5;7;1) deux vecteurs.
u→+v→(-2;8;3).
Coordonnées de tu→
Soient u→(x;y;z) un vecteur
et t un nombre réel.
On a tu→(tx:ty;tz).
Exemple
Soient u→(5;-4;7) un vecteur et t=-3.
On a -3u→(-15;12;-21).