Etude des fonctions numériques (12)
Exercice 1 tp
Soit f une fonction définie par
| f(x) = | 1 | x -1 + √(x+2) |
| 2 |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
1) Déterminer D le domaine de définition de f et
calculer la limite de f en +∞.
2) (a) Déterminer une direction asymptotique (Δ) à la courbe (C)
(b) Etudier les positions relatives de la droite (Δ) et la courbe (C).
3) Montrer que (C) admet une demi-tangente verticale au point d'abscisse -2.
4) (a) Montrer que (∀x∈D\{-2})
| f '(x) = | 1 | (1+ | 1 | ) |
| 2 | √(x+2) |
(b) Déduire les variations de f et tracer son tableau de variations.
5) (a) Tracer la courbe (C).
(b) Résoudre graphiquement l'équation f(x)=0 et donner un encadrement de la solution.
(c) Déduire le signe de la fonction f.
Correction
1) D={x∈IR/ x+2≥0}=[-2;+∞[
lim +∞ |
f(x) = | lim +∞ |
1 | x-1+√(x+2) |
| 2 | ||||
=lim +∞ |
1 | x-1+ | lim +∞ |
√(x+2) |
| 2 |
lim +∞ |
1 | x-2 = +∞ ⇒ | lim +∞ |
√(x+2) = +∞ |
| 2 |
| donc | lim +∞ | f(x) = +∞+∞ = +∞ |
| 2) (a) On a | lim +∞ | f(x) = +∞ |
lim +∞ |
f(x) | = | lim +∞ |
1 | - | 1 | + | √(x+2) |
| x | 2 | x | x |
| = | lim +∞ |
1 | - | 1 | +√( | 1 | + | 2 | ) |
| 2 | x | x | x² |
| on a | lim +∞ |
1 | = | lim +∞ |
1 | = 0 |
| x | x² |
| donc | lim +∞ |
f(x) | = | 1 |
| x | 2 |
lim +∞ |
f(x)- | 1 | x | = | lim +∞ |
-1+√(x+2)=+∞ |
| 2 |
ainsi la courbe (C) admet une branche parabolique de direction la droite
| (Δ): y = | 1 | x |
| 2 |
(b) Positions relatives de (C) et (Δ)
| f(x) - | 1 | x | = -1+√(x+2) |
| 2 |
Signe de -1+√(x+2).
-1+√(x+2)≥0 ⇔√(x+2) ≥ 1
⇔ x+2 ≥ 1 ⇔ x ≥ -1
donc (C) est au-dessus de (Δ) sur [-1;+∞[ et (C) est au-dessous sur [-2;-1].
3) Dérivation en -2+
on a f(-2)=-2
lim -2+ |
f(x)+2 | = | lim -2+ |
x+2+2√(x+2) |
| x+2 | 2(x+2) |
| = | lim -2+ |
1 | + | √(x+2) |
| 2 | (x+2) | |||
| = | lim -2+ |
1 | + | 1 |
| 2 | √(x+2) |
lim -2+ |
f(x)+2 | = | 1 | + | 1 | = +∞ |
| x+2 | 2 | 0+ |
et cela signifie que f n'est pas dérivable au point -2 et de plus (C) admet une demi-tangente verticle au point d'abscisse -2.
4) (a) La fonction x→x+2 est un polynôme donc dérivable sur IR et en particulier sur l'intervalle I=]-2;+∞[ et de plus elle est strictement positive sur I donc la fonction x→√(x+2) est dérivable sur I=]-2;+∞[.
La fonction
| x→ | 1 | x - 1 |
| 2 |
est un polynôme donc dérivable sur IR et en particulier sur l'intervalle I=]-2;+∞[
ainsi la fonction f est dérivable sur I.
Soit x∈I
| f '(x) = ( | 1 | x | -1 + √(x+2))' |
| 2 | |||
| = | 1 | + | 1 |
| 2 | 2√(x+2) |
| f '(x) = | 1 | (1+ | 1 | ) |
| 2 | √(x+2) |
(b) (∀x∈D\{-2}): √(x+2)>0 donc f'(x)>0 donc f est strictement croissante sur D.
| x | -2 | +∞ | |
| f '(x) | + | ||
| f | -2 |
↗ |
+∞ |
5) (a) la courbe (C)
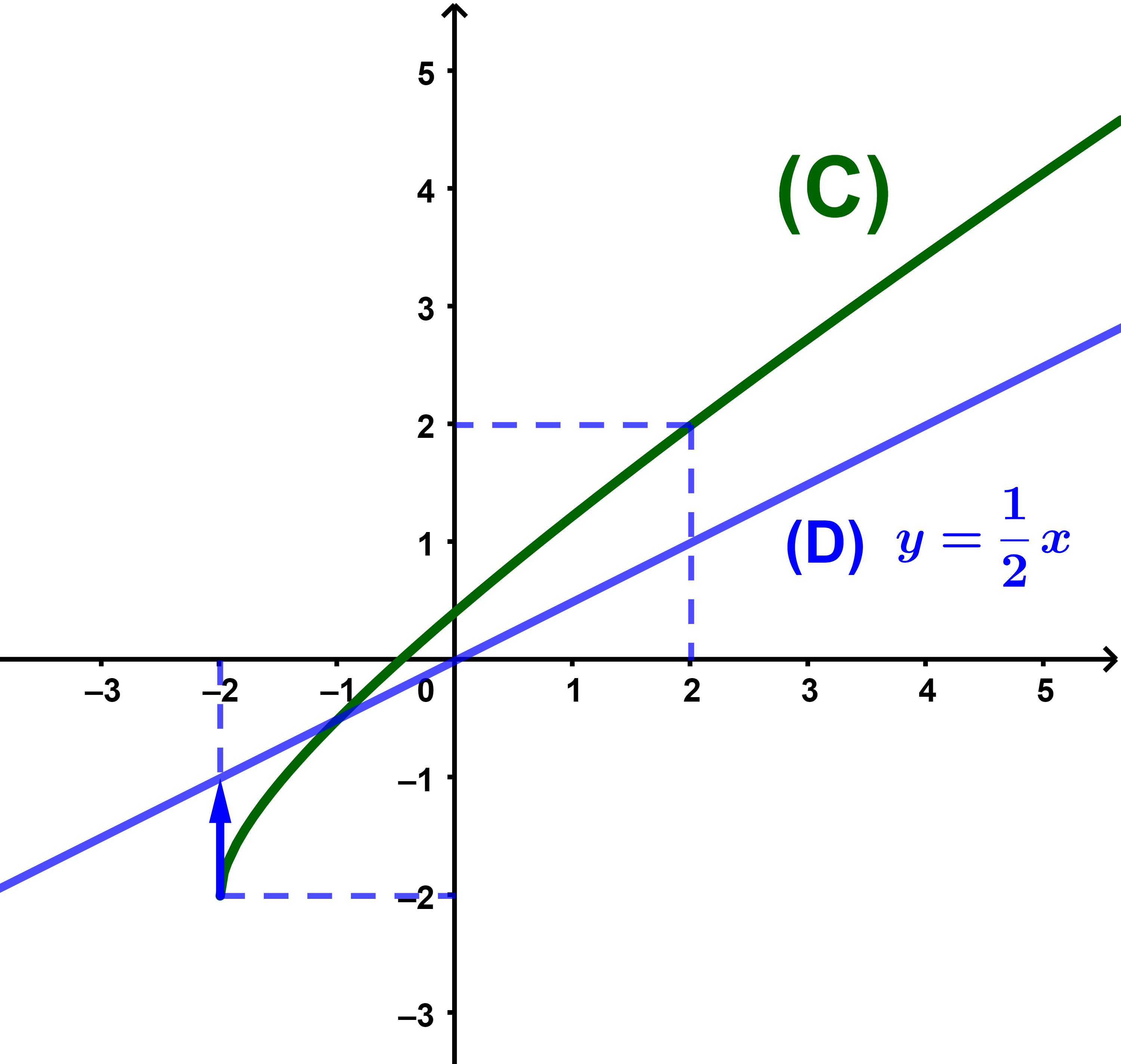
(b) La courbe (C) coupe l'axe des abscisses en un seul point donc l'équation f(x)=0 admet une seule solution, notée a avec -1<a<0.
(c) La courbe (C) est au-dessous de l'axe des abscisses sur l'intervalle [-2;a] et au-dessus de l'axe des abscisses sur l'intervalle [a;+∞]
ainsi f est positive sur [a;+∞.
et négative sur l'intervalle [-2;a].
| x | -2 | a | +∞ | ||||
| f(x) | - | 0 | + |