2 تقعر دالة ونقط انعطاف

2.1 تقعر منحنى دالة

2.1.1 تعريف

لتكن f دالة عددية قابلة للاشتقاق على I و (C) المنحنى الممثل لها في معلم
اذا كان المنحنى (C) فوق جميع مماساته على المجال I فان المنحنى Cf محدبا على المجال I
(تقعره موجه نحو الاراتيب الموجبة)
واذا كان المنحنى (C) تحت جميع مماساته على المجال I فان المنحنى (C) مقعرا على المجال I
(تقعره موجه نحو الاراتيب السالبة)

2.1.2 مثال

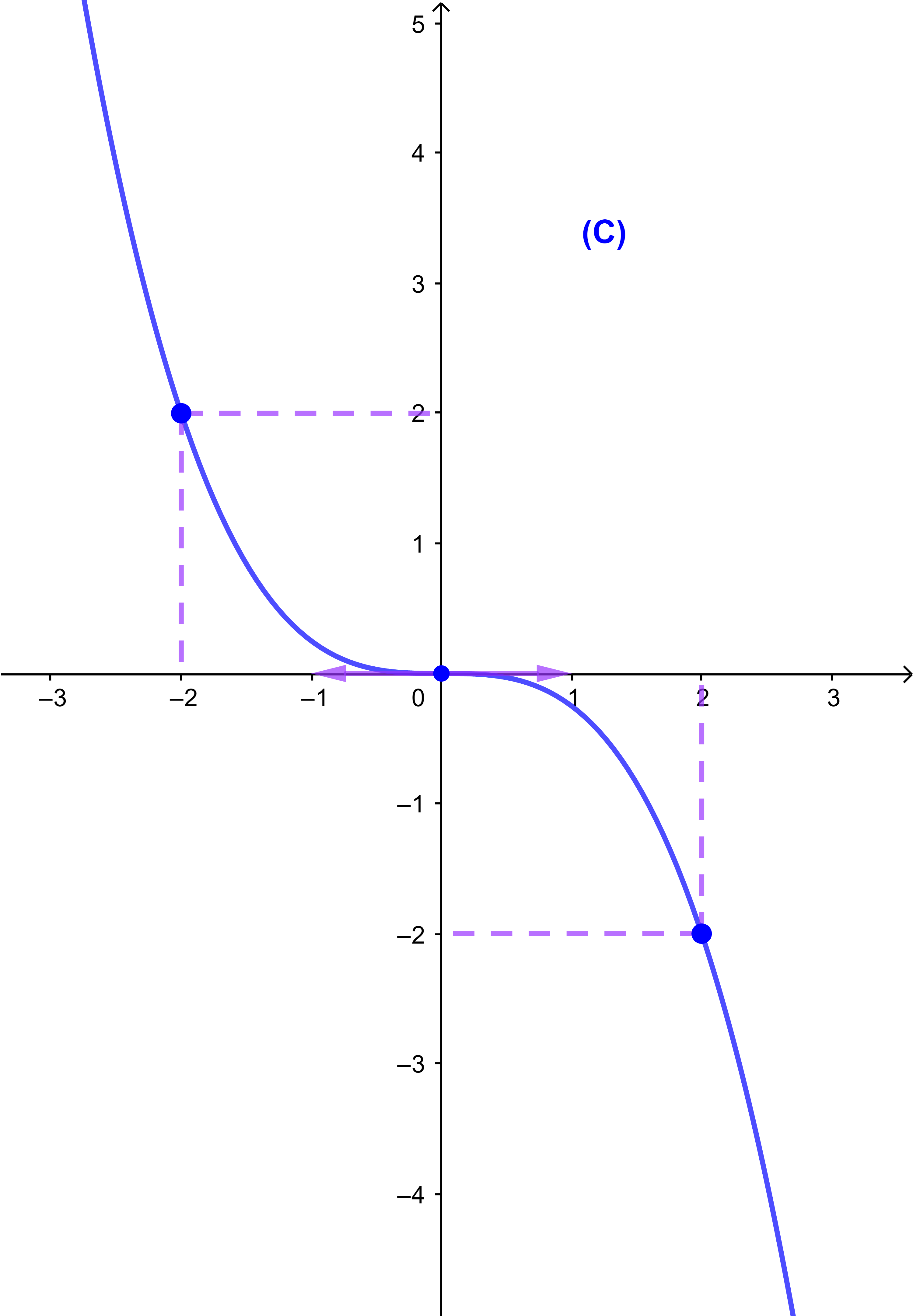
لتكن f دالة عددية معرفة كما يلي f(x)=x³ لدينا f حدودية اذن قابلة للاشتقاق على IR
والمنحنى (C) يوجد فوق جميع مماساته على IR+ , نقول اذن المنحنى (C) محدبا على IR+
والمنحنى (C) يوجد تحت جميع مماساته على IR- , نقول اذن المنحنى (C) مقعرا على IR-

تمرين

ماذا يمكن القول عن تقعر المنحنى (Cg) بحيث g(x)= -x³ ?

2.2 نقطة الانعطاف

2.2.1 تعريف

لتكن f دالة عددية قابلة للاشتقاق على مجال I و a∈I و (C) المنحنى الممثل لها في معلم
نقول ان نقطة A(a;f(a)) نقطة انعطاف للمنحنى (C )اذا كان تقعر (C) يتغير في النقطة A

مثال

لتكن f دالة عددية معرفة بما يلي f(x)= x³, النقطة O نقطة انعطاف للمنحنى (C)

خاصيات

لتكن f دالة عددية قابلة للاشتقاق مرتين على مجال I و (C) منحناها في معلم (O;i^→;j^→)
اذا كان ∀x∈I : f"(x)≥0 فان المنحنى (C) محدب
اذا كان ∀x∈I : f"(x)≤0 فان المنحنى (C) مفعر
اذا كان ∀x∈I : f"(a)=0 و f" تغير اشارتها في a
فان A(a;f(a)) نقطة انعطاف للمنحنى

3- عناصر تماثل منحنى دالة

3.1 الزوجية

3.1.1 خاصية

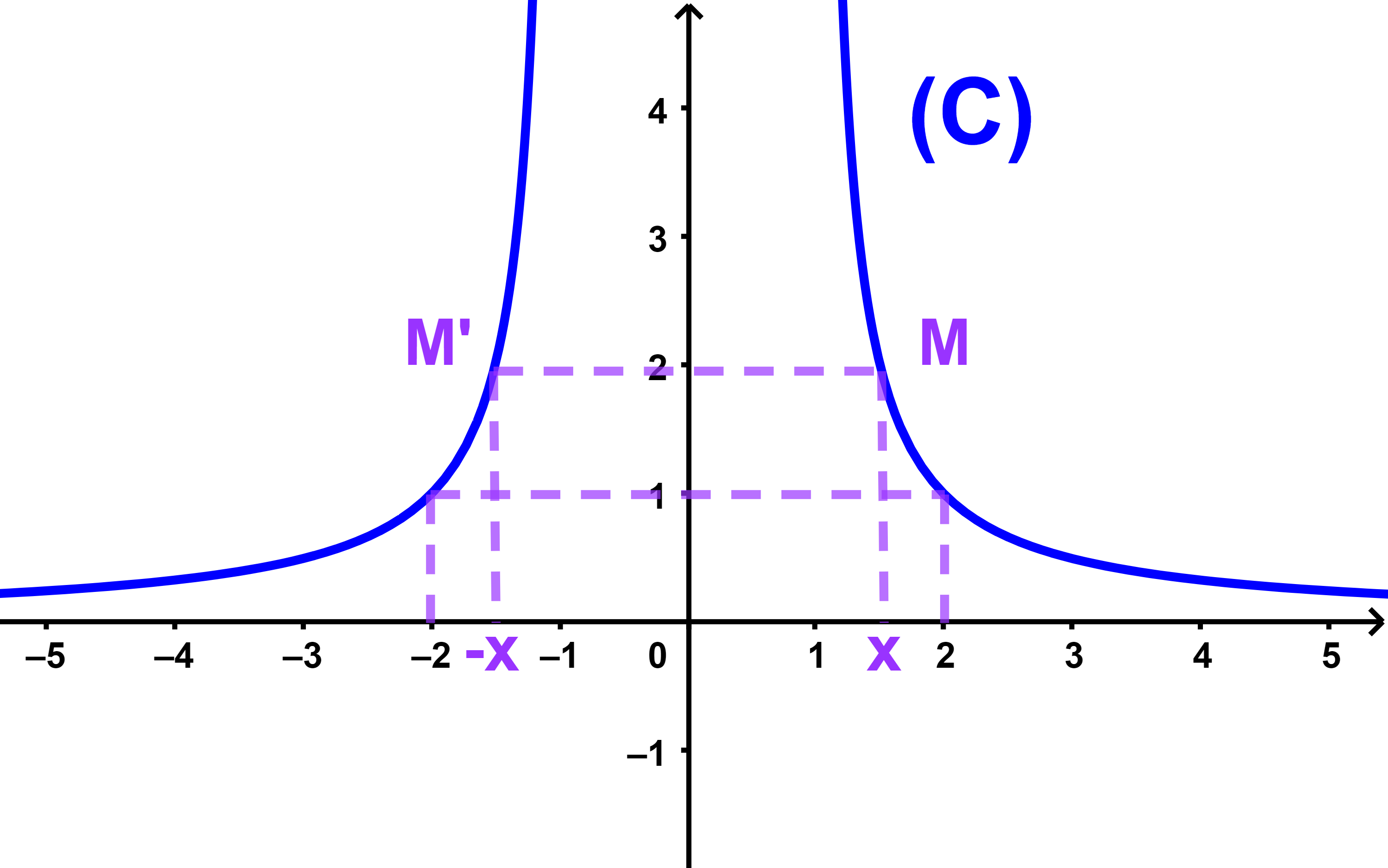
اذا كانت f دالة زوجية فان منحناها (C) مماثل بالنسبة لمحور الاراتيب

3.1.2 خاصية

اذا كانت f دالة زوجية فان منحناها (C) مماثل بالنسبة لاصل المعلم

3.2 الدورية

3.2.1 تذكير

نقول ان دالة f دورية دورها T اذا تحقق ما يلي
1) لكل x∈D لدينا x+T و x-T∈Df
2) لكل x∈D لدينا f(x+T)=f(x)

3.2.2 خاصية

اذا كانت f دالة دورية دورها T فانه يمكن دراستها على مجال سعته T ونرسم منحناها (C) في هذا المجال الذي سعته T ثم نتمم الرسم باستعمال الازاحة ذات المتجهة u^→=Ti^→

مثال

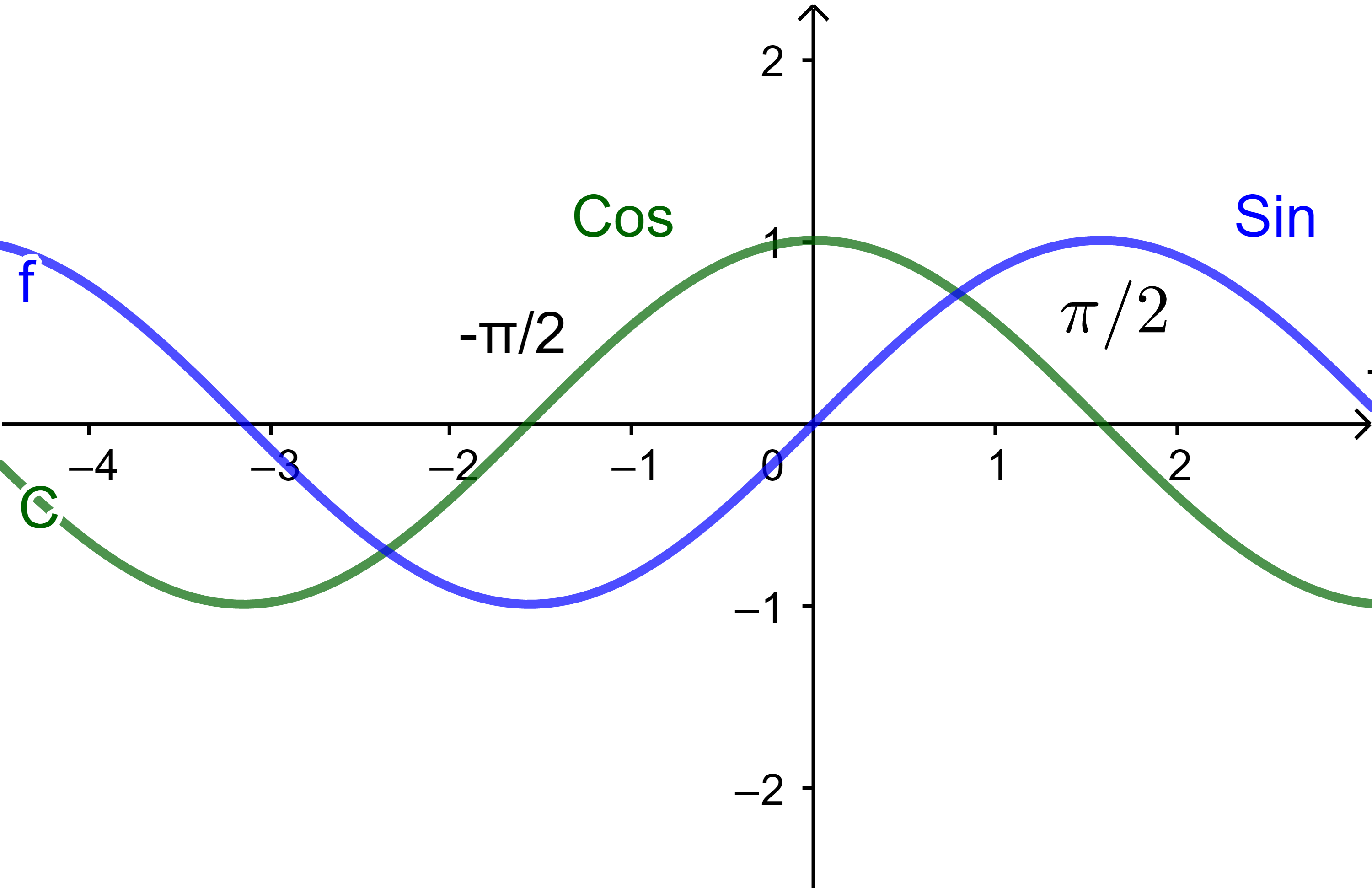
الدالتان cos و sin دوريتان ولهما نفس الدور يساوي 2π اذن يمكن دراستهما على مجال سعته 2π
فليكن [-π;π] او [0;2π] ..

3.3 محور تماثل

خاصية

لتكن f دالة عددية لمتغير حقيقي x و D مجموعة تعريفها و (C) المنحنى الممثل لها في معلم متعامد ممنظم المستقيم (D) الذي معادلته x=a محور تماثل للمنحنى (C) اذا تحقق ما يلي
1) ليكن x∈D لدينا 2a-x∈D
2) ليكن x∈D لدينا f(2a-x)=f(x)

3.4 مركز تماثل

3.4.1 خاصية

لتكن f دالة عددية لمتغير حقيقي x و D مجموعة تعرفها و (C) المنحنى الممثل لها في معلم متعامد ممنظم
النقطة A(a;b) مركز تماثل للمنحنى (C) اذا تحقق ما يلي
1) ليكن x∈D لدينا 2a-x∈D
2) ليكن x∈D لدينا f(2a-x)=2b-f(x)

3.4.2 مثال

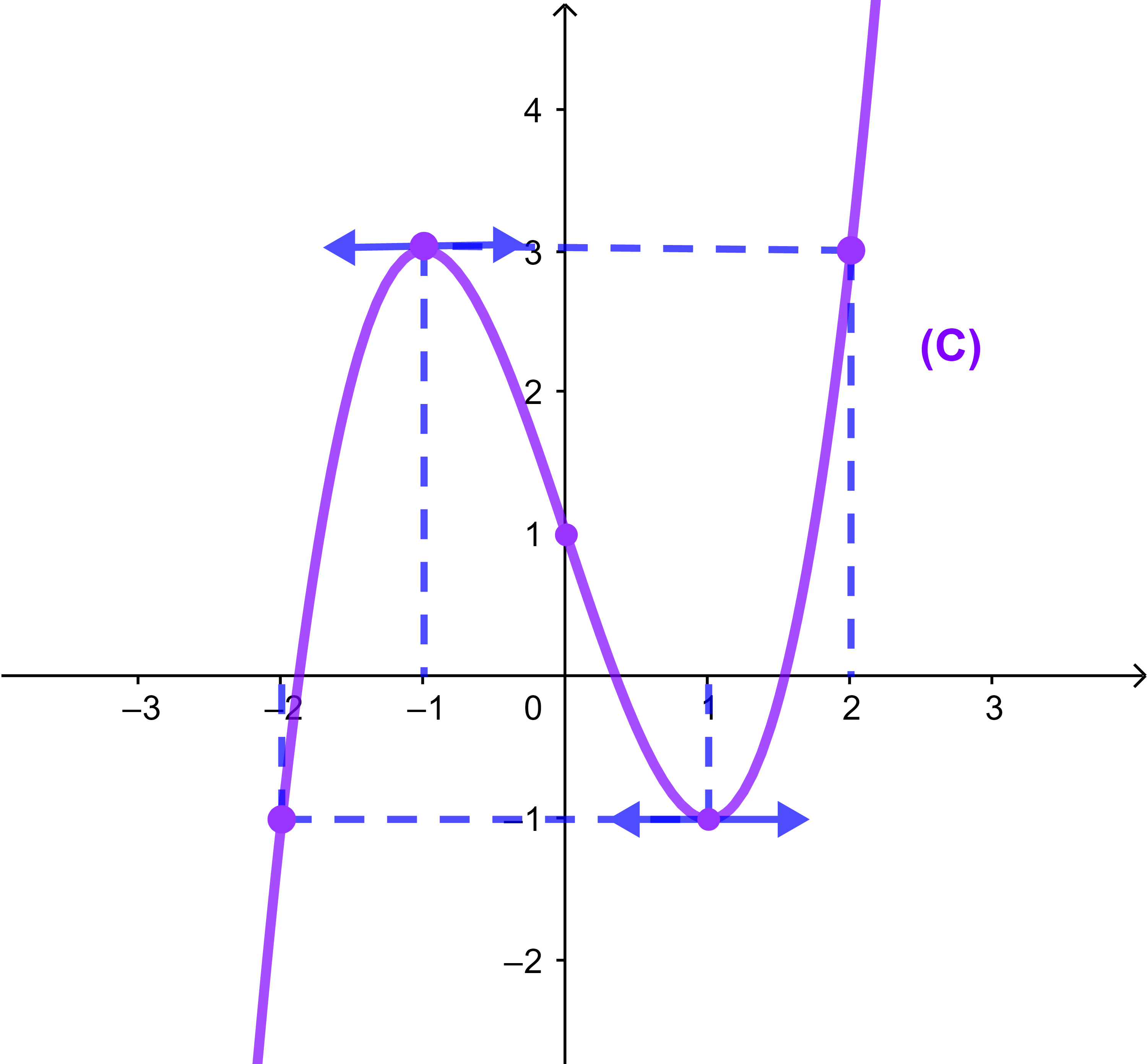
لتكن f دالة عددية معرفة كالتالي f(x)=x³-3x+1
بين ان A(0;1) مركز تماثل منحنى الدالة f

تمرين 1

لتكن f دالة عددية معرفة كالتالي f(x)=x³-3x
1) حدد مركز تماثل منحنى الدالة f
2) حدد مجال الدراسة المختصر للدالة f
3) ادرس رتابة الدالة وانشئ جدول تغيراتها
4) انشئ منخنى الدالة f في معلم متعامد ممنظم

تمرين 2

لتكن f دالة عددية معرفة كالتالي

f(x)=x+1+	1
	x

1) احسب النهايات عند محدات الدالة f
2) حدد مقاربات الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم

تمرين 3

لتكن f دالة عددية معرفة كالتالي

f(x)=	x²+x-1
	2x-2

1) احسب النهايات عند محدات الدالة f
2) حدد مقاربات الدالة منحنى الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) حل مبيانيا وجبريا المتراجحة f(x)≤0

تمرين 4

نعتبر الدالة f المعرفة ب f(x)=2x-2 +√(x-1)
1) احسب نهايات الدالة f عند محداتها ثم حدد اتجاه مقارب لمنحنى الدالة f
2) ادرس قابلية الاشتقاق للدالة f في 1 ثم ادرس رتابة الدالة f وانشئ جدول تغيراتها
3) انشئ منحنى الدالة f في معلم متعامد ممنظم

تمرين 5

نعتبر الدالة f المعرفة ب

f(x)=x+	2
	√(x-1)

1) احسب نهايات الدالة f عند محداتها ثم حدد مقاربا للمنحنى (C)
2) حل في IR المعادلة (x-1)√(x-1)-1=0
3) احسب f'(x) ثم ادرس اشارتها على مجموعة تعريفها وانشئ جدول تغيراتها
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) حل حسب قيم العدد m المعادلة f(x)=m مبيانيا