دراسة دوال عددية (2)
تمرين 5 tp
لتكن f دالة عددية معرفة كالتالي
| f(x)= | x²+x-1 |
| 2x-2 |
2) حدد مقاربات منحنى الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) حل مبيانيا المتراجحة f(x)≥0
تصحيح
1) لدينا D={x∈IR / 2x-2≠0} =]-∞;1[∪]1;+∞[
| lim -∞ | f(x)= | lim -∞ | x² | lim -∞ | 1 | x | = -∞ |
| 2x | 2 | ||||||
| lim +∞ | f(x)= | lim +∞ | x² | lim +∞ | 1 | x | = +∞ |
| 2x | 2 |
| lim -∞ | f(x) | = | lim -∞ | x² | = | 1 |
| x | 2x² | 2 |
| lim -∞ | f(x)- | 1 | x = | lim -∞ | 2x-1 | = 1 |
| 2 | 2x-2 |
اذن المنحنى (C) يقبل مقارب مائل بجوار -∞ معادلته
| y = | 1 | x + 1 |
| 2 |
| lim +∞ | f(x) | = | lim +∞ | x² | = | 1 |
| x | 2x² | 2 |
| lim +∞ | f(x)- | 1 | x = | lim +∞ | 2x-1 | = 1 |
| 2 | 2x-2 |
| y = | 1 | x + 1 |
| 2 |
3) f دالة جذرية اذن قابلة للاشتقاق على مجموعة تعريفها D=IR\{1}
| f'(x) = | 2x²-4x | 2x(x-2) |
| (2x-2)² |
f تزايدية قطعا على ]-∞;0] وعلى [2;+∞[ و تناقصية قطعا على [0;1[ وعلى ]1;2]
| x | -∞ | 0 | 1 | 2 | +∞ | |||||
| f'(x) | + | 0 | - | - | 2 | + | ||||
| f | -∞ | ↗ | 1/2 | ↘ | -∞ |
+∞ | ↘ | 5/2 |
↗ | +∞ |
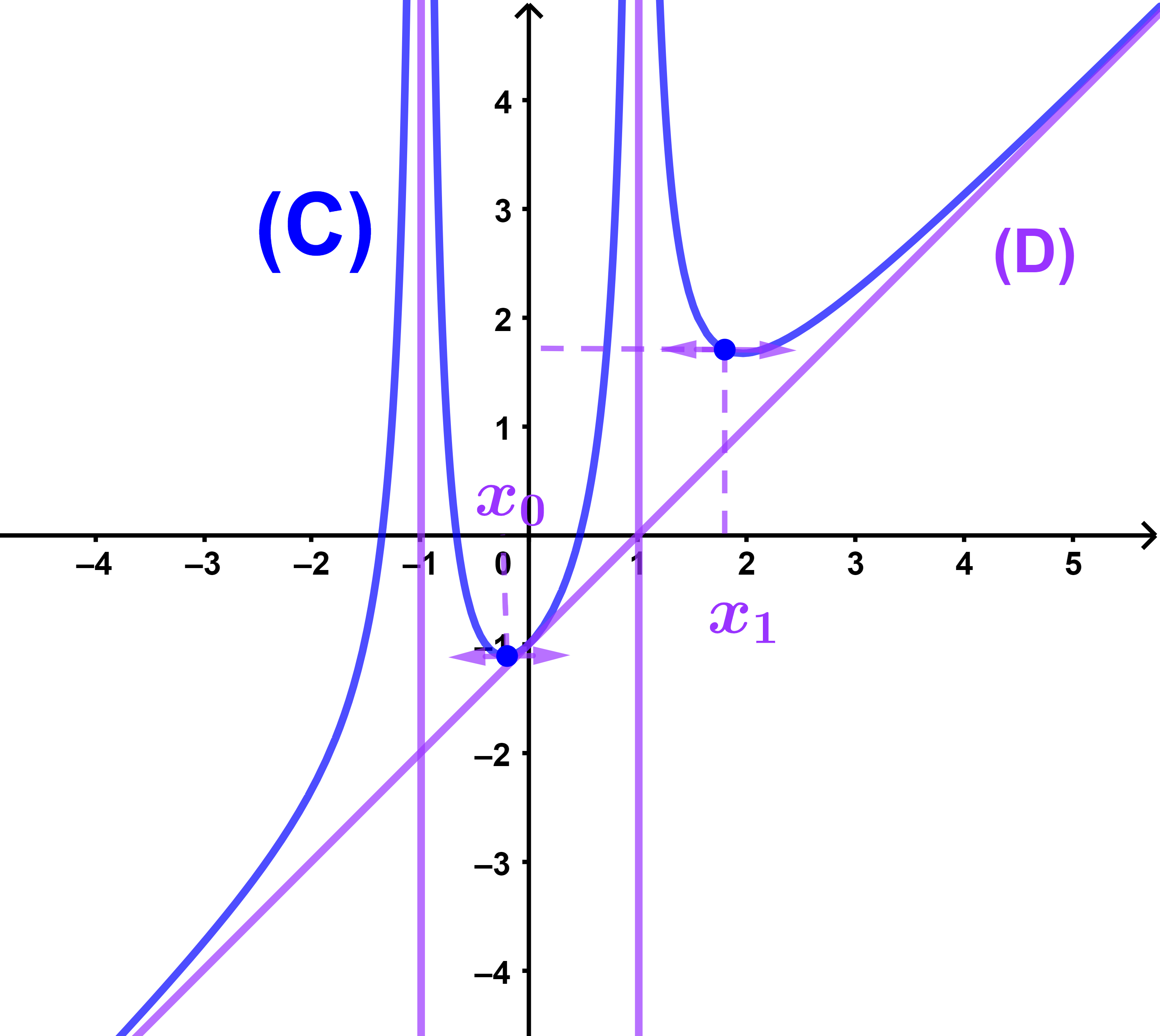
5) منحنى الدالة يقطع محور الافاصيل في نقطتين اذن المعادلة تقبل حلين مختلفين نرمزلهما ب a1 و a2 حيث
-2< a1< -1 و
0< a2< 1
الحل المبياني للمتراجحة f(x)≥ 0 هو مجموعة افاصيل نقط المنحنى الموجودة فوق محور الافاصيل وبذلك
S=[a1 ; a2]∪]1;+∞[
تمرين 6 tp
لتكن f دالة عددية معرفة كالتالي
| f(x)= x - | x |
| x²-1 |
2) حدد مقاربات منحنى الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) حل مبيانيا المتراجحة f(x)≥0
تمرين 7 tp
لتكن f دالة عددية معرفة كالتالي
| f(x)= x + | | x²+1 | | |
| x²-1 |
2) حدد مقاربات منحنى الدالة f
3) احسب f'(x) حيث x∈]-∞;-1[∪]1;+∞[
و f'(x) حيث x∈]-1;1[
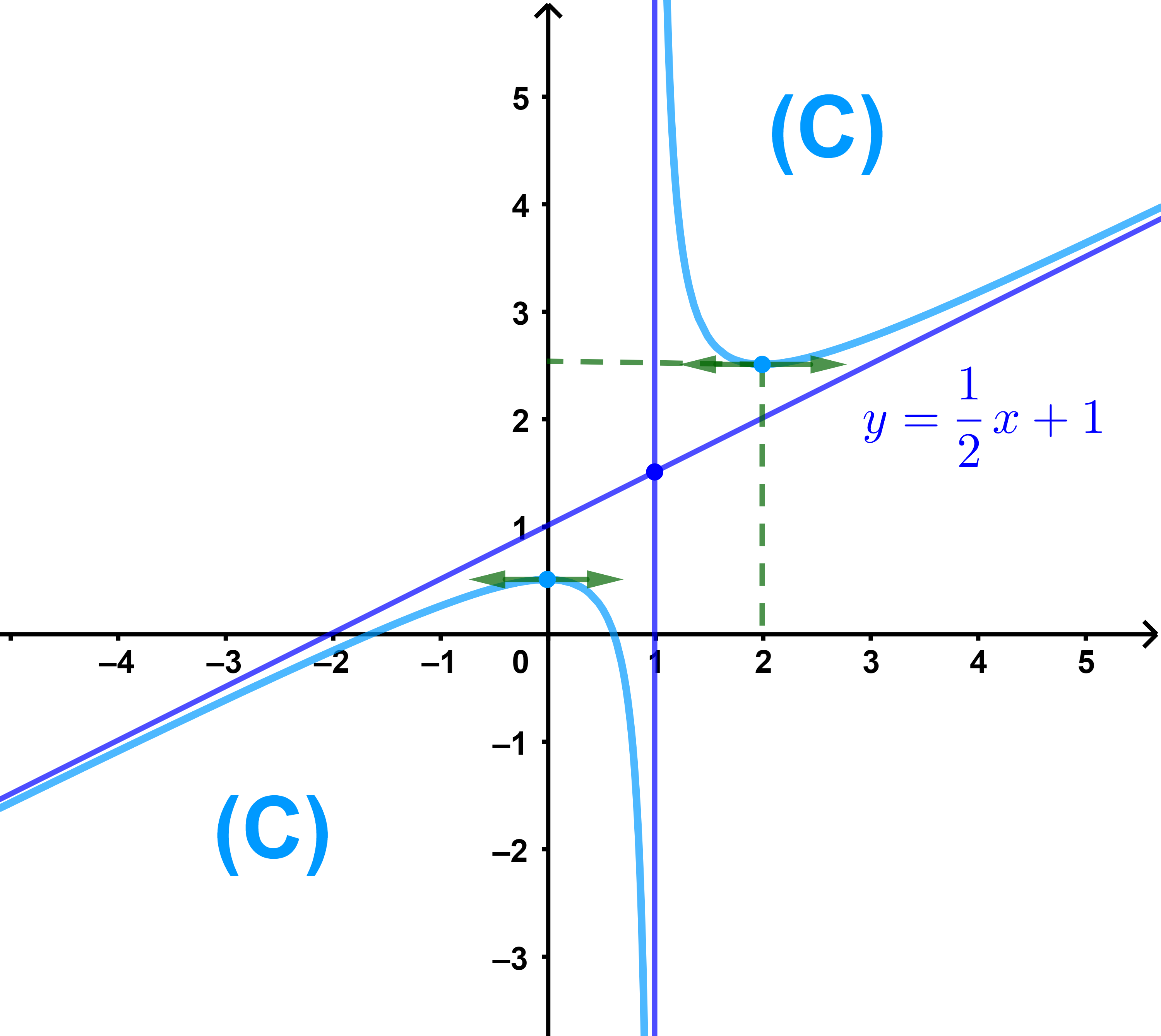
4) ليكن (C) منحنى الدالة f في معلم متعامد ممنظم اسفله
ادرس رتابة الدالة من خلال المنحنى f وانشئ جدول التغيرات
5) حل مبيانيا وحسب قيم الوسيط m المعادلة f(x)=m.
