تمرين

نعتبر الدالة f المعرفة كما يلي f(x)=√(x²+1)
1) ادرس زوجية الدالة f
2) ادرس رتابة الدالة f على IR+ ثم استنتج الرتابة على IR-

تصحيح

1) D=IR لان لكل x∈IR لدينا x²+1≥0
اذن لكل x∈IR لدينا (-x)∈IR
f(-x)=√((-x)²+1)=√(x²+1)=f(x)
وهذا يعني ان الدالة f زوجية

2) نلاحظ ان الدالة f هي مركب الدالتين r=√ و p:x→x²+1
f=rop
Dr=IR+ ; Dp=IR ;p(IR)⊂IR+
لان ∀x∈IR, p(x)>0
الدالة p تزايدية على IR+ والدالة √ تزايدية كذلك على IR+ اذن المركب f هو كذلك تزايدي على IR+
وبما ان الدالة f زوجية وتزايدية على IR+ فهي اذن تناقصية على IR-

3- التمثيلات المبيانية

3.1 الدالة: x→√(x+a)

3.1 مثال 1

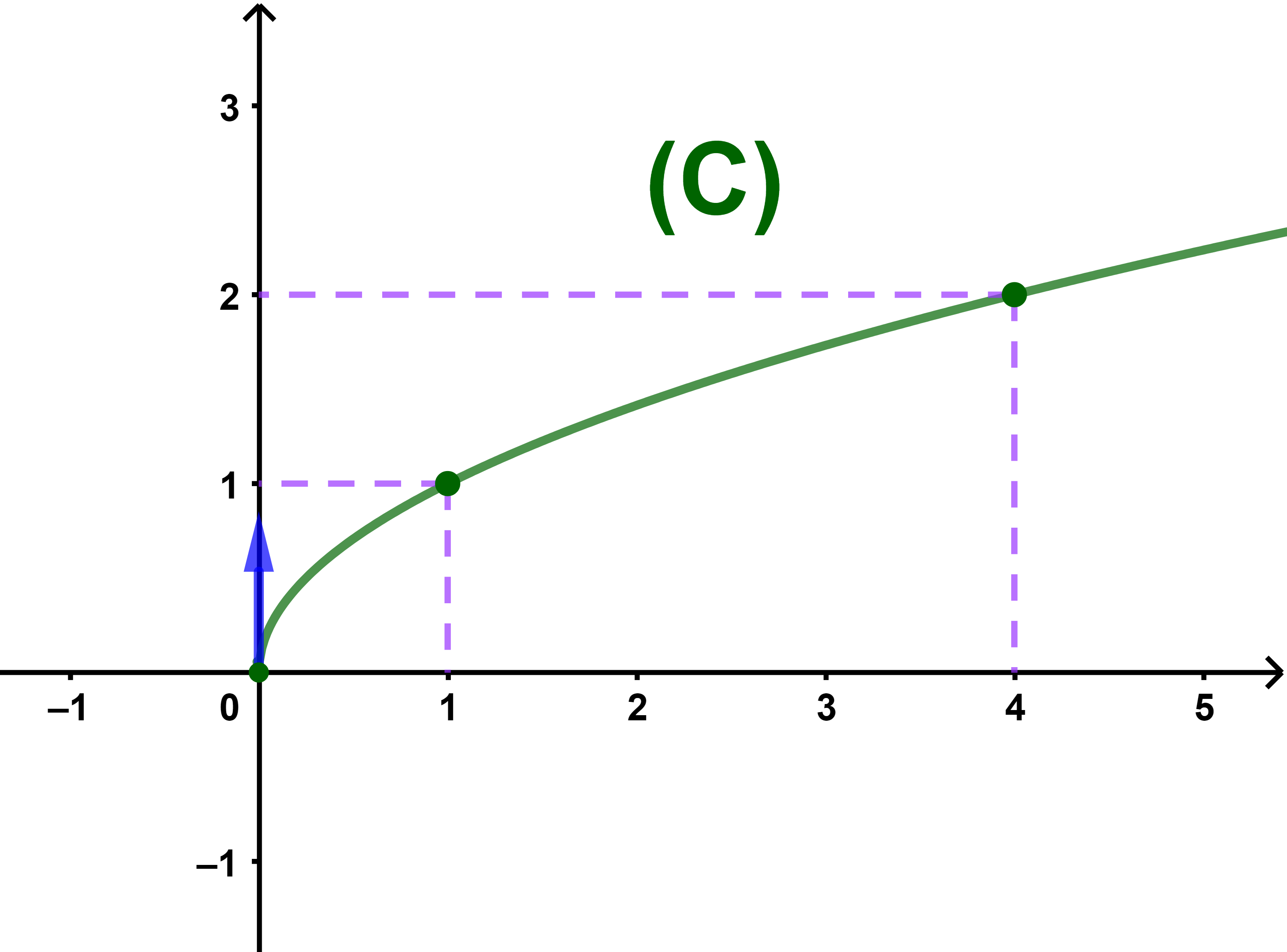
لتكن f دالة معرفة كما يلي f(x)=√(x)
ادرس الدالة f.

3.1.2 مثال 2

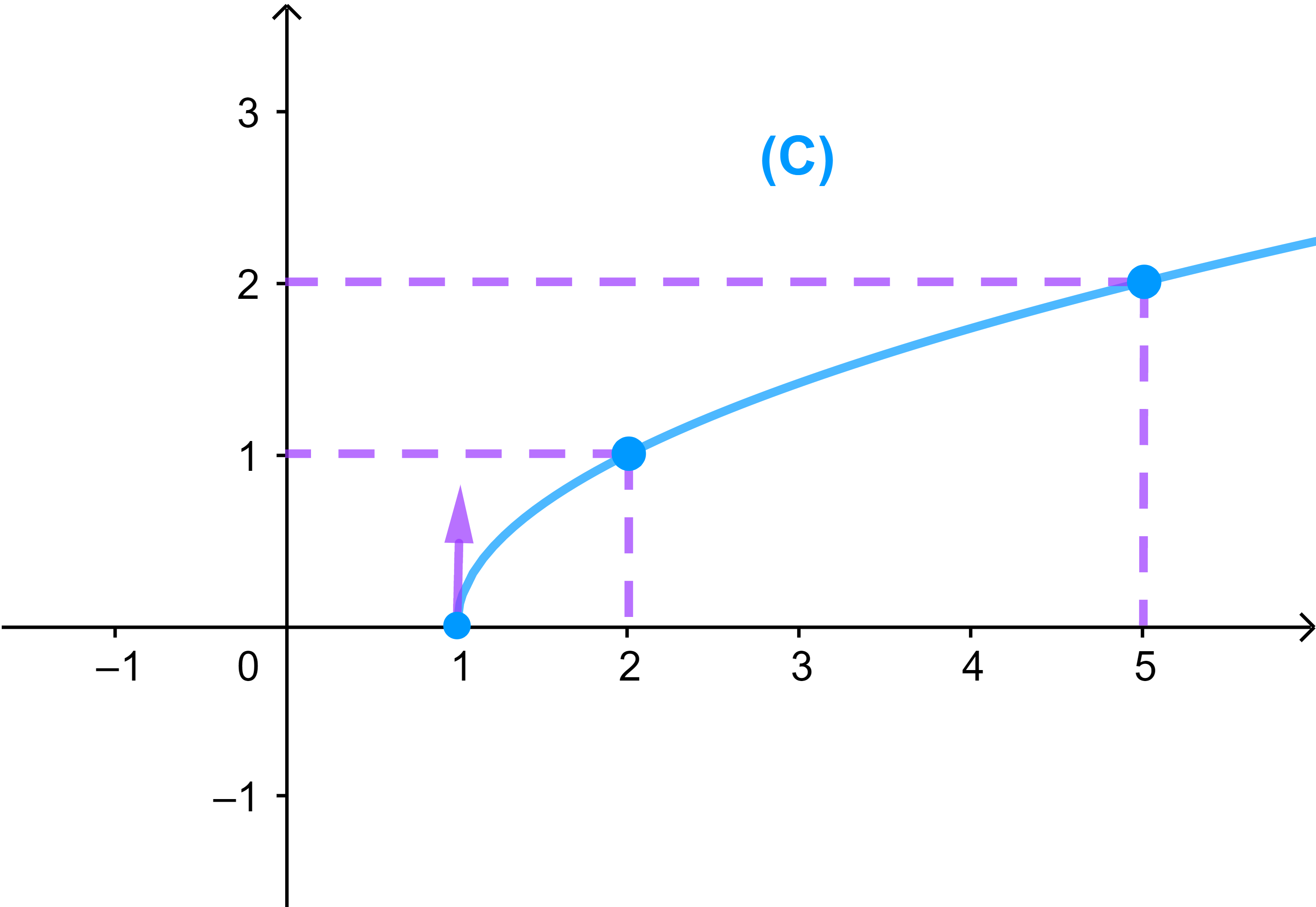
لتكن f دالة معرفة كما يلي f(x)=√(x-1)
ادرس الدالة f.

3.1.3 مثال 3

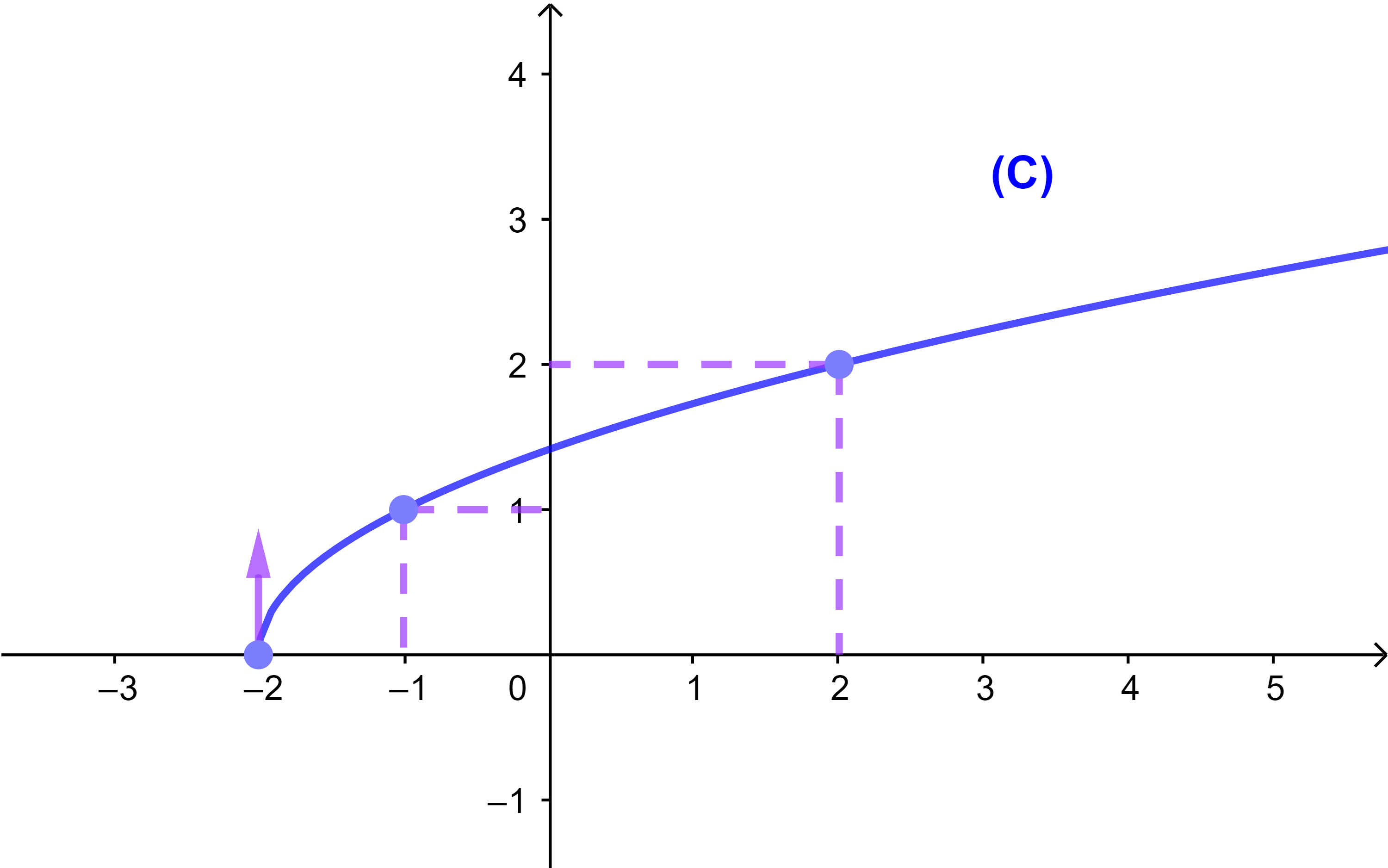
لتكن f دالة معرفة كما يلي f(x)=√(x+2)
ادرس الدالة f

3.2 الدالة: x→ax³

3.2.1 مثال 1

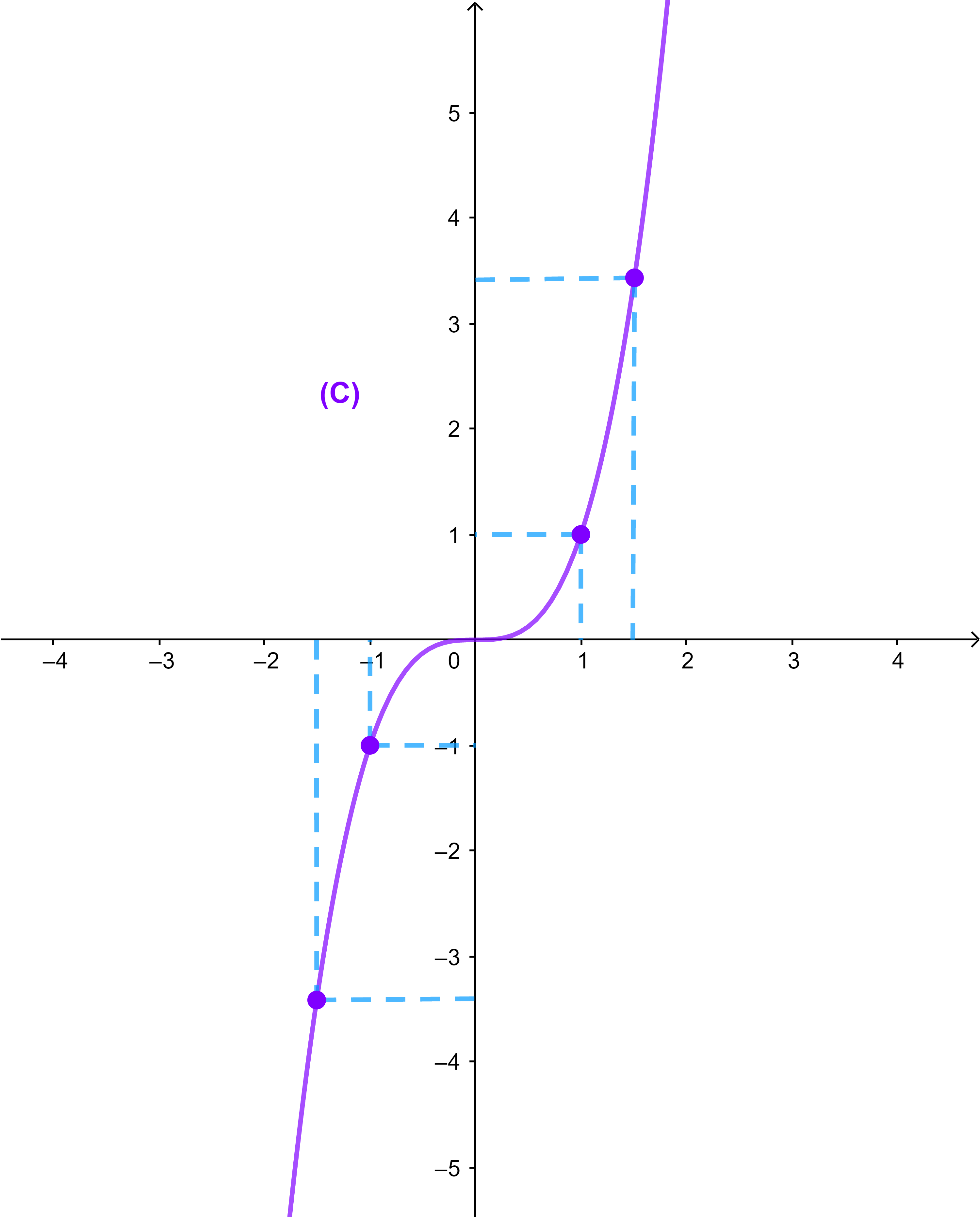
لتكن f دالة معرفة كما يلي f(x)=x³
ادرس الدالة f

3.2.2 مثال 2

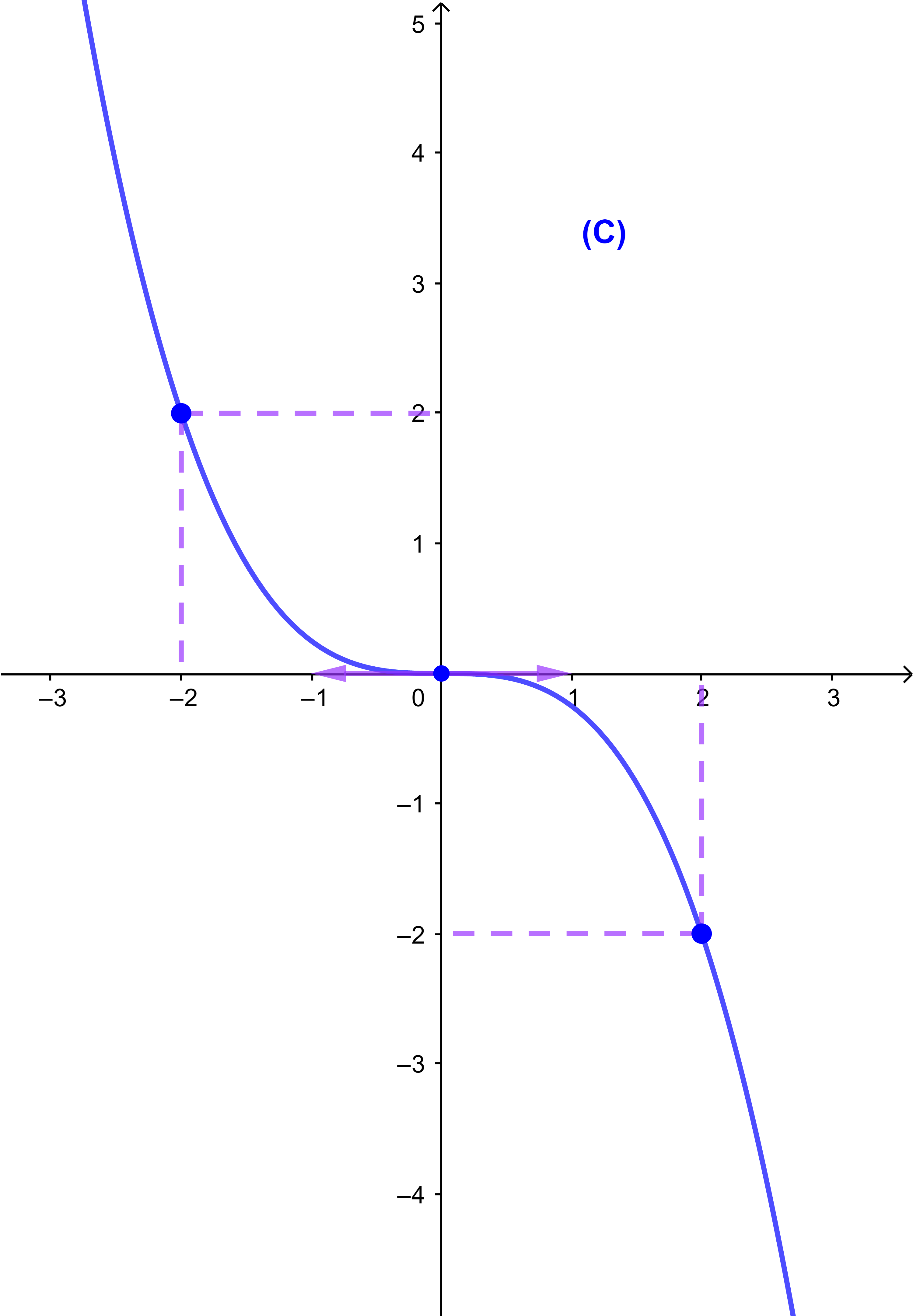
لتكن f دالة عددية معرفة كما يلي f(x)=-(0,25)x³
ادرس الدالة f

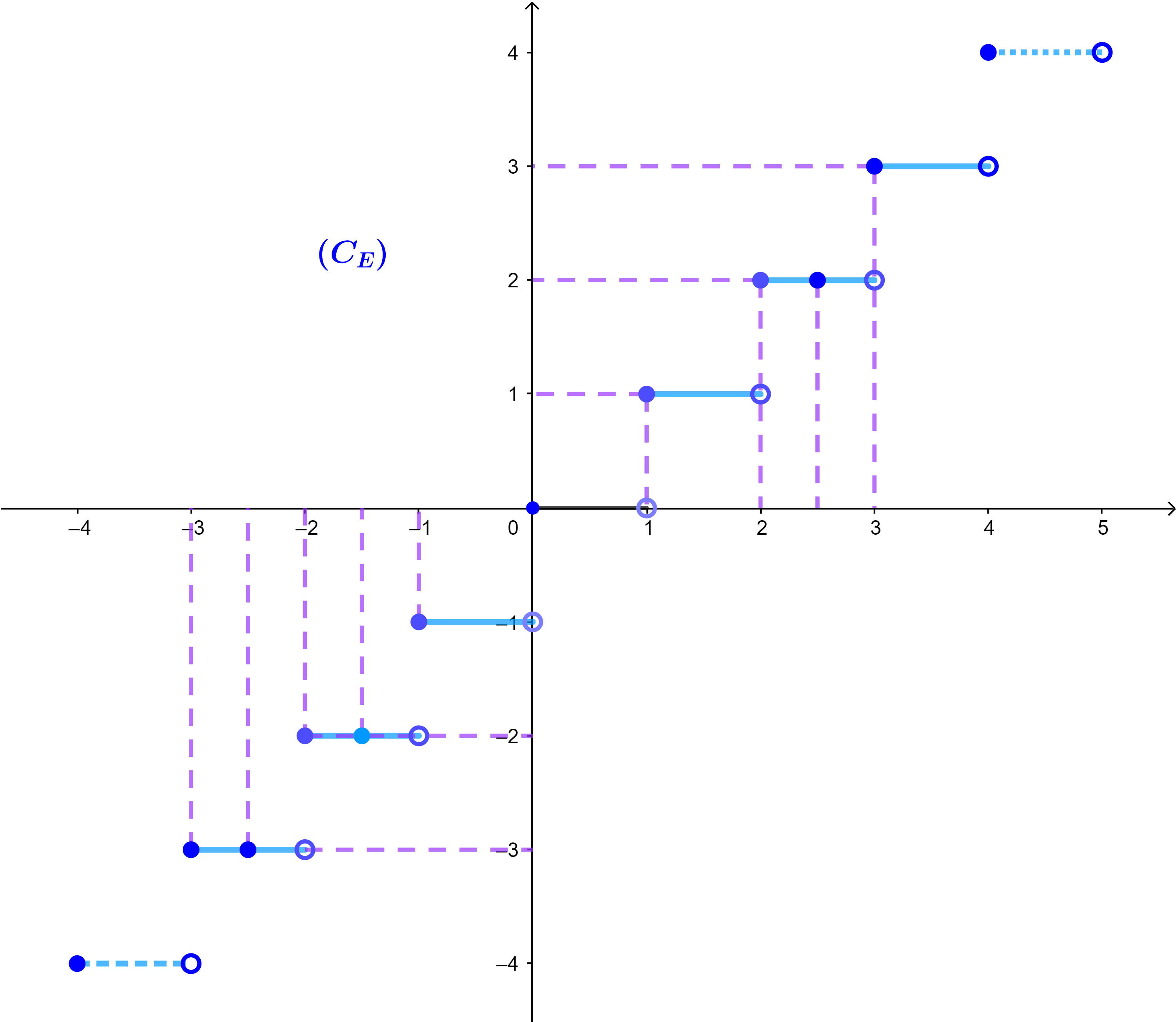
3.3 الدالة: x→E(x)

دالة الجزء الصحيح معرفة على قطع شبه مفتوحة على اليمين [i;i+1[; i∈ℤ
مجموعة تعريفها هي IR.
∀x∈IR; ∃!p∈ℤ:
p≤x<p+1, E(x)=p
مثال: اذا كان x∈[-2;-1[ فان E(x)=-2
واذا كان x∈[3;4[ فان E(x)=3