Généralités sur les fonctions (4)
1.4 Extremums d’une fonction
1.4.1 Valeur minimale et valeur maximale
Soit f une fonction numérique définie sur un intervalle I et a∈I.
1) La valeur minimale de f est la plus petite des images de f.
En d'autre terme f(a) est une valeur minimale de f
⇔ (∀x∈I): f(x)≥f(a).
2) La valeur maximale de f est la plus grande des images de f.
En d'autre terme f(a) est une valeur maximale de f
⇔ (∀x∈I): f(x)≤f(a).
3) Toute valeur minimale ou maximale d'une fonction f est appelée extremum de f.
1.4.2 Exemple 1
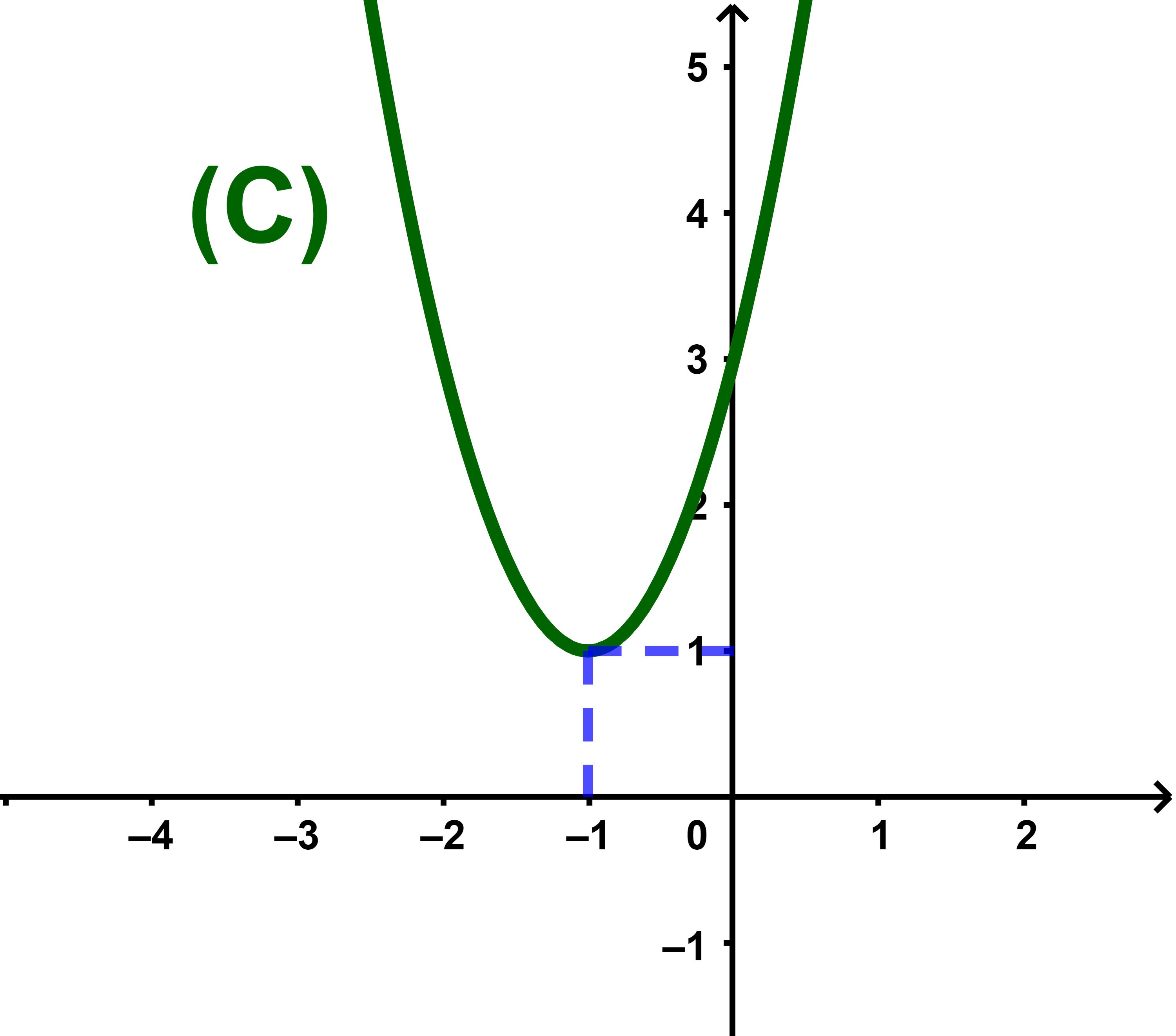
Soit f une fonction numérique définie par
f(x)=x²+1.
Montrer que 1 est une valeur minimale de f.
Correction
Soit x∈IR on a x²≥0 donc x²+1≥1
ainsi (∀x∈IR): f(x)≥1.
Il reste à savoir s'il existe un élément a∈I=IR tel que f(a)=1 ?
il suffit donc de résoudre l'équation f(x)=1 dans I.
f(x)=1 ⇔ x²+1=1 ⇔ x²=0.
⇔ x=0
ainsi 1=f(0) est une valeur minimale de f.
1.4.3 Exemple 2
Soit f une fonction numérique définie par
f(x)=-x²+3.
Montrer que 3 est une valeur maximale de f.
Correction
Soit x∈IR on a -x²≤0 donc
-x²+1≤3
ainsi (∀x∈IR): f(x)≤3.
Il reste à savoir s'il existe un élément a∈I=IR tel que f(a)=3 ?
il suffit donc de résoudre l'équation f(x)=3 dans I.
f(x)=3 ⇔ -x²+3=3 ⇔ x²=0
donc x=0 ainsi 3=f(0) est une valeur maximale de f.
Exercice 1 tp
Soit f une fonction numérique définie par
f(x)=2x²+4x+3.
Montrer que 1 est un extremum de f.
Correction
Soit x∈IR.
f(x)-1=2x²+4x+3-1
= 2x²+4x+2 =2(x²+2x+1)=2(x+1)² ≥0
donc (∀x∈IR): f(x)≥1.
On cherche un élément a∈I=IR s'il exist tel que f(a)=1 ?
il suffit donc de résoudre l'équation f(x)=1 dans I.
f(x)=1 ⇔ f(x)-1=0
⇔ 2(x+1)²=0 ⇔ x=-1
donc 1=f(-1) est une valeur minimale de f
ainsi 1 est un extremum de f atteint en -1.