4- تفكيك دوران ومركب دورانين

4.1 تفكيك دوران

4.1.1 البناء

ليكن r(W;α) دورانا في المستوى
نعتبر مستتقيما (D) مارا من W ومستقيما آخرا (D') مارا من W
بحيث mes((D);(D'))= θ+kπ; k∈Z
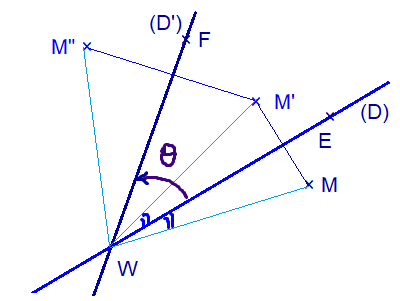
S و S' تماثلان محوريان محوراهما على التوالي (D) و (D')
M نقطة من المستوى و S(M)=M' و S'(M')=M"
اذن
S'oS(M)=M"
لدينا من جهة اولى
WM=WM'=WM" ...
ومن جهة أخرى
(WM;WM")=(WM;WM')+(WM';WM")+ 2kπ
= 2(WE;WM')+2(WM';WF)+2kπ (انظر الى الشكل )
=2(WE;WF) + 2kπ
لدينا اذن WM=WM" و (WM;WM")=2θ+2kπ ومنه فان S'oS دورانا مركزه W وزاويته 2θ

r=SoS' اذن 2θ= α
يكفي اذن اخذ θ=(α/2)+2kπ

4.1.2 خاصية 1

ليكن D(W;u) ; D'(W;u') مستقيمين متقاطعين و S و S' تماثلين محوريين محوراهما على التوالي (D) و (D')
S'oS دورانا مركزه W وزاويته 2(u^→ ; u'^→)

4.1.3 خاصية 2

الدوران هو مركب تماثلين محوريين ومتقاطعين في مركز هذا الدوران

4.2 مركب دورانين

4.2.1 البناء

ليكن r(W;α) و r(W';α') دورانين
اذن r = SoS1 و r' = S1oS'
ror' = SoS1oS1oS' (D1;D)=α/2 +kπ
W من D1 و D
(D';D1) = α'/2 +kπ
W' من D' و D1
وبما ان W≠W' فان (D1)=(WW')
ror' = sos'
(D';D) = (α+α')/2 + kπ ; α+α'≠2π