تمرين 1 tp

نعتبر EAB ; ECD مثلثين متساويي الساقين وقائمي الزاوية في E
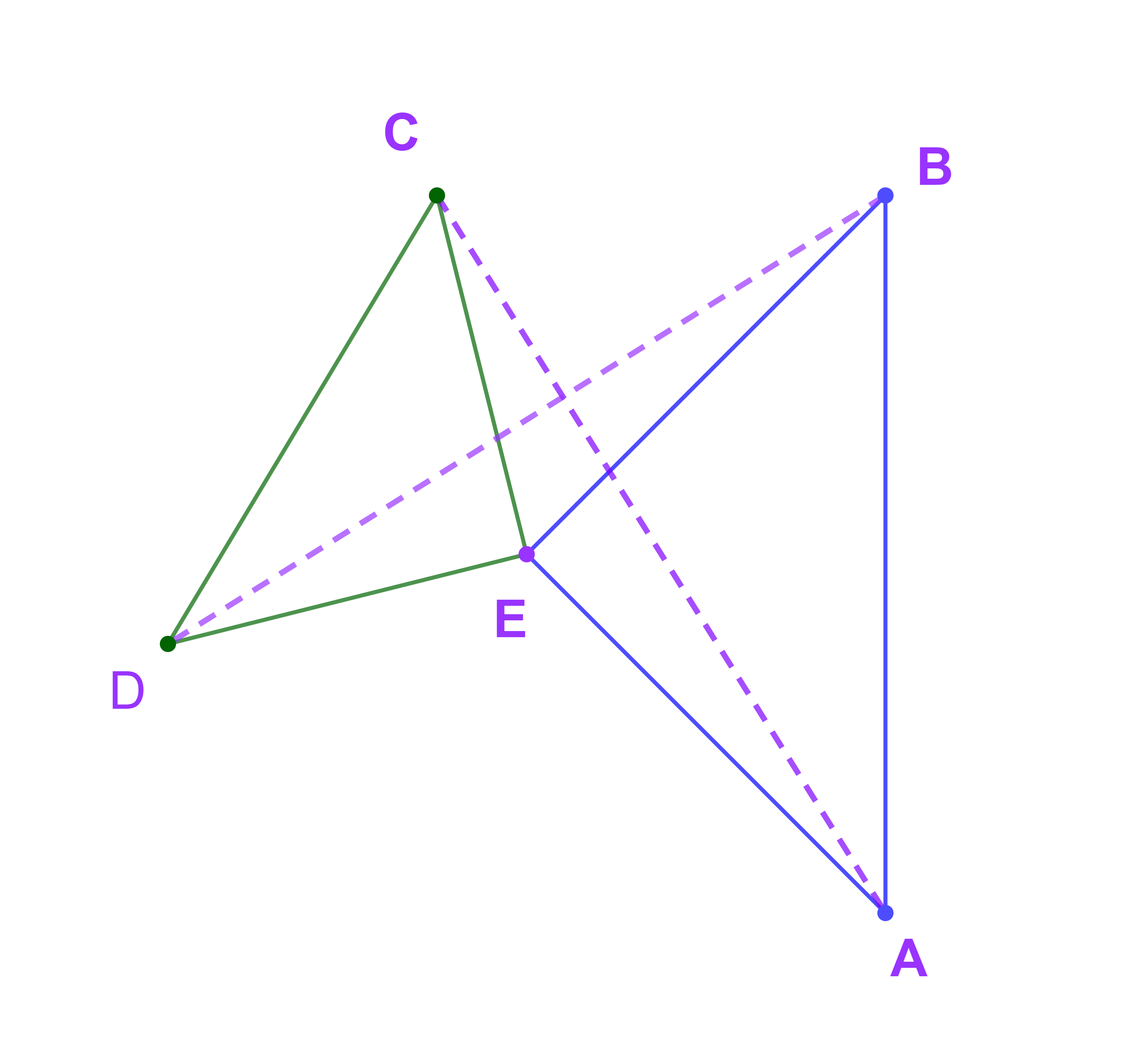1) حدد دورانا r يحول A الى B ويحول C الى D
2) بين ان َِAC=BD
3) ما هو الوضع النسبي للمستقيمين (AC) ; (BD).

تمرين 2 tp

ليكن ABC مثلثا متساوي الساقين وقائم الزاوية في A

(CA;CB)≡	π	[2π] و
	4

1) انشئ الشكل
2) حدد مركز وزاوية الدوران r الذي يحول C الى B و I الى A حيث C منتصف القطعة [AI]

تصحيح

1)

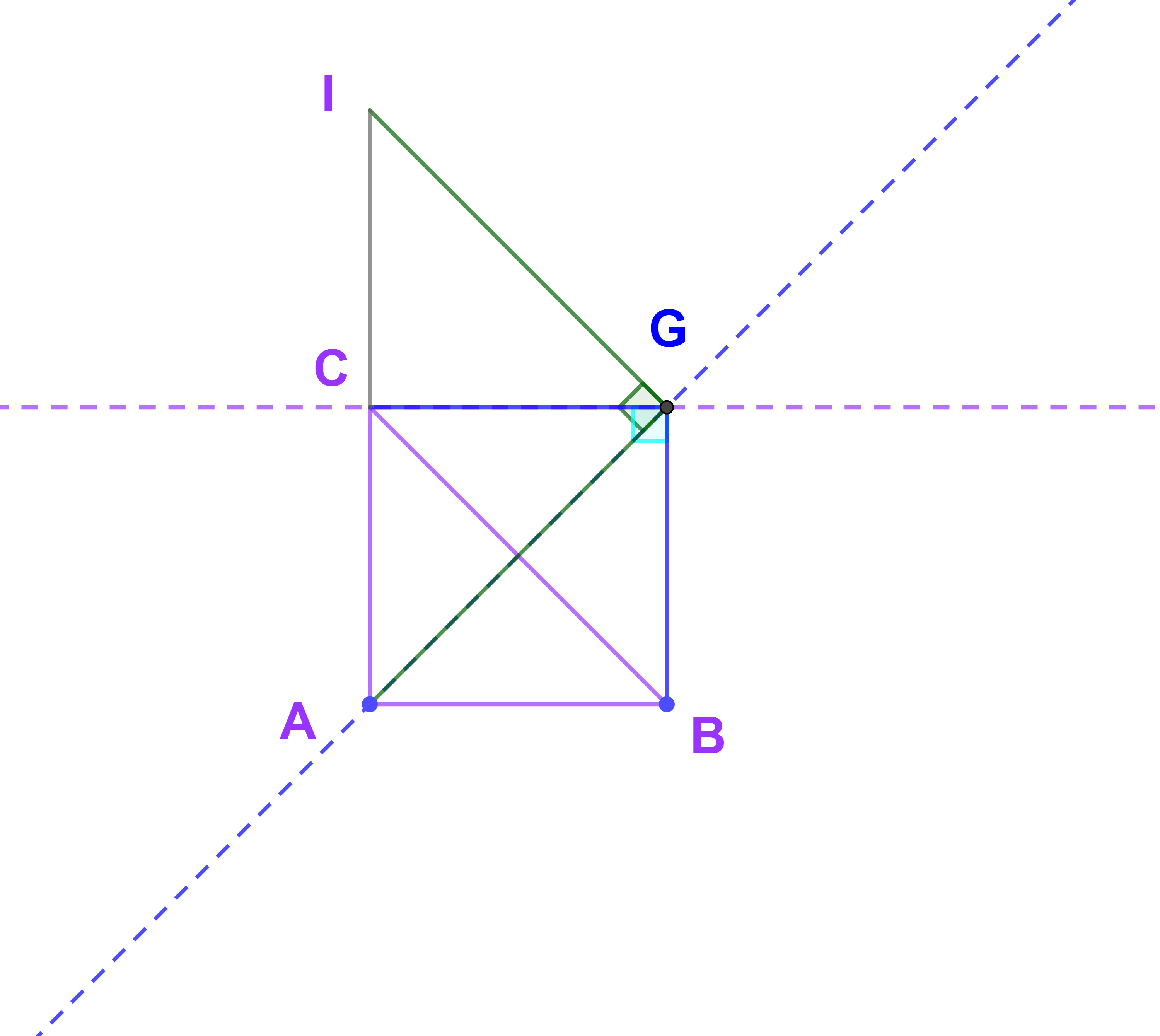
2) نرمز ب G لمركز الدوران r
r(B)=C ⇒ G∈med(BC)
r(A)=I ⇒ G∈med(AI)
اذن med(BC)∩med(AI)={G}

لدينا ايضا med(BC)=(AG) لان ABC متساوي الساقين وبالاضافة انه قائم الزاوية في A

(AG;AC)≡	π	[2π] فان
	4

ومنه فان

(GC;GA)≡	π	[2π]
	4

وبالتالي زاوية الدوران r

α ≡	π	[2π]
	2

تمرين 3 tp

ليكن ABCD مربعا و E ; F نقطتين خارج الربع بحيث EAB ; FBC مثلثين متساويي الاضلاع بحيث الزاوية (EA;EB) موجهة توجيها موجبا 1) انشئ الشكل
2) نعتبر r دورانا مركزه E وزاويته

π

3

(q1) تحقق ان r(A)=B
(q2) بين ان r(D)=F
2) ما طبيعة المثلث EDF

تصحيح

1) 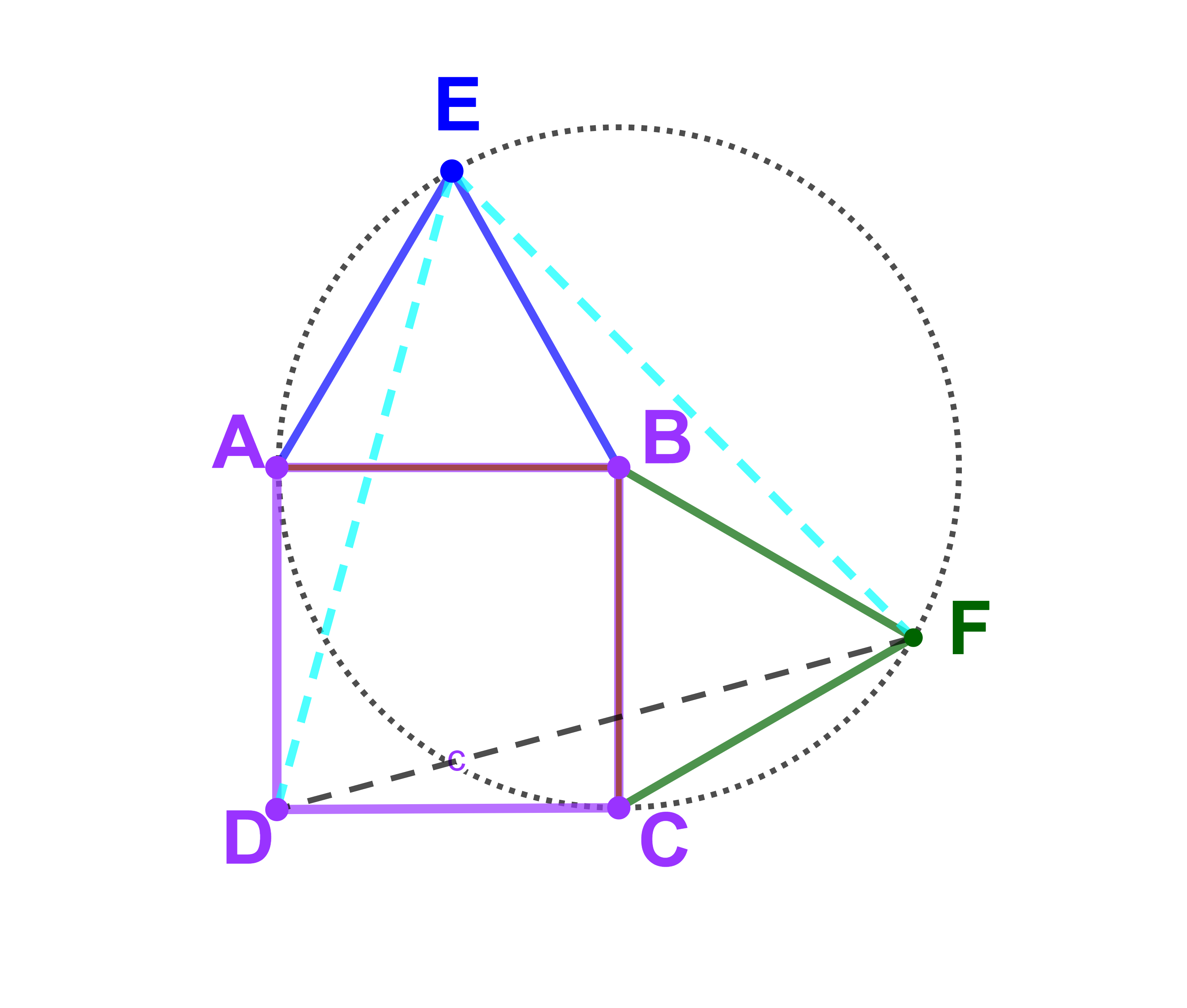2) (q1) لدينا EAB مثلثا متساوي الاضلاع اذن

{	(EA;EB)≡	π	[2π]
		3
	EA=EB

وهذا يعني ان r(A)=B
(q2) نبين ان r(D)=F
لدينا المثلث AED متساوي الساقين رأسه A لان AE=AD
ولدينا BEF متساوي الساقين رأسه B لان BE=BF
للبرهنة على ان ED=EF يكفي ان نبين ان الزاويتين [EAD] ; [EBF] لهما نفس القياس نعلم ان

(EA;ED)≡	π	+	π	≡	5π
	2		3		6

ولدينا

(BF;BE)≡2π -	π	-	2π	≡	5π
	2		3		6

اذن (BF;BE)≡ (EA;ED)[2π] ومنه فان

{	(ED;EF)≡	π	[2π]
		3
	ED=EF

وبالتالي r(D)=F
3) المثلث EDF متساوي الاضلاع لان