Dérivation (2)
1.1.4 Dérivée à gauche et dérivée à droite
Dérivée à gauche
Soit f une fonction définie sur un intérvalle
sous la forme [a;a+r[.
f est dérivable à droite à a s'il existe un nombre réel L tel que
lim x→a+ |
f(x)-f(a) | = L |
| x-a |
L est appelé le Nombre dérivé de f à droite à a et est noté f'd(a) .
| f'd(a) = | lim x→a+ |
f(x)-f(a) |
| x-a |
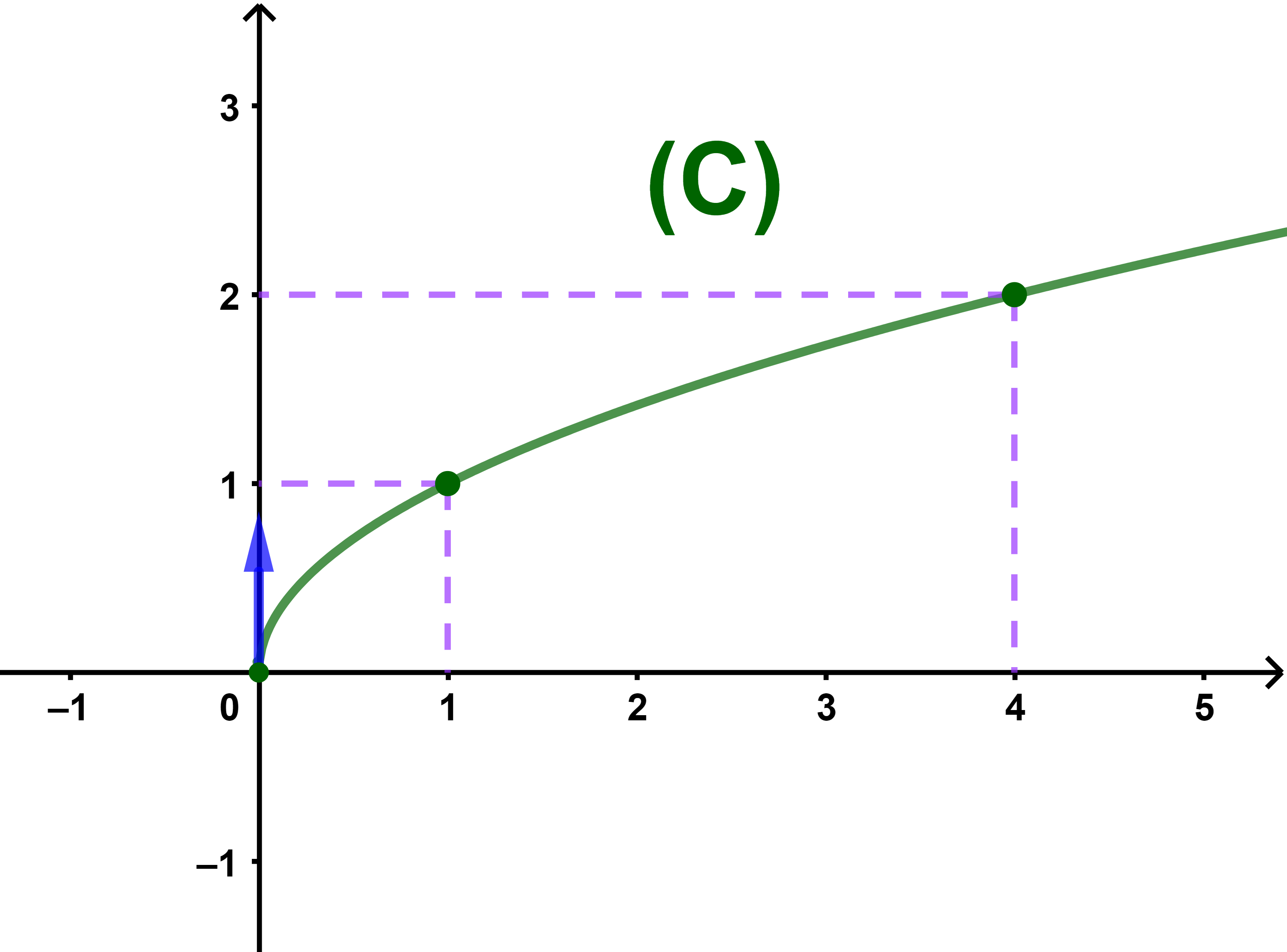
Exemple Dérivabilité de la fonction f=√ en 0+
lim x→0+ |
f(x)-f(0) | = | lim x→0+ |
√(x) |
| x | x |
| = | lim x→0+ |
1 | = +∞ | |
| √(x) |
f n'est pas dérivable en 0+.
Dérivée à gauche
Soit f une fonction définie sur un intérvalle
sous la forme ]a-r;a].
f est dérivable à gauche à a s'il existe un nombre réel L tel que
lim x→a- |
f(x)-f(a) | = L |
| x-a |
L est appelé le Nombre dérivé de f à gauche à a et set noté f'g(a) .
| f'g(a) = | lim a- |
f(x)-f(a) |
| x-a |
Propriété
f est dérivable au point a équivaut à
f est dérivable à droite et à gauche à a
et f'd(a)=f'g(a).
Exemple
Soit f une fonction définie par
| { | f(x) = | 2x²+4x+3 | si x <-2 |
| f(x) = | x²-1 | si x ≥ -2 |
f(-2)=(-2)²-1=3.
lim -2- |
f(x)-f(-2) | = | lim -2- |
2x²+4x+3-3 |
| x+2 | x+2 | |||
| =lim -2+ |
2x(x+2) | = | lim -2+ |
2x=-4 |
| x+2 |
f est donc dérivable à gauche à (-2) et f'g(-2)=-4.
lim -2+ |
f(x)-f(-2) | = | lim -2+ |
x²-4 |
| x+2 | x+2 |
| = | lim -2+ |
x-2 = -4 |
f est dérivable à droite à -2 et f'd(-2)=-4.
f'd(-2)=f'g(-2)=-4 ⇒ f est dérivable en -2.
Interprétation de la demi-tangente
Le plan est rapporté à un repère orthonormé (O;i→;j→). Soit f une fonction et (C) sa courbe représentative.
1) f est dérivable à droite à a signifie que (C)
admet une demi tangente au point A(a,f(a)) d'équation
y=f'd(a)(x-a)+f(a).
2) f est dérivable à gauche à a signifie que
(C) admet une demi tangente au point
A(a,f(a)) d'équation
y=f'g(a)(x-a)+f(a).
3) Si f n'est pas dérivable à droite (ou à gauche) au point a
et
lim x→a± |
f(x)-f(a) | = ±∞ |
| x-a |
alors la (C) admet une demi-tangente verticle au point A(a;f(a)).
Exemple
La courbe de la fonction f définie par f(x)=√(x)
admet une demi-tangente verticale au point O.