1- المجموعة المنتهية

1.1 تعريف وترميز

1.1.1 امثلة

نعتبر المجموعة التالية
E = {-2 ; 3; 7 ; 10},
هي مجموعة مكونة من خمس عناصر اذن E هي مجموعة منتهية
نعتبر المجموعة التالية
F={x ∈IR/ x>0}
هي مجموعة مكونة من ما لانهاية من العناصر اذن فهي مجموعة غير منتهية

1.1.2 تعريف

نقول ان مجموعة منتهية اذا كان عدد عناصرها هو عددا حقيقيا اي (منتهيا)

1.1.3 ترميز

عدد عناصر مجموعة منتهية , E, يسمى رئيسي المجموعة E, ونرمز له ب cardE .

1.1.4 مثال

E={-3;-1;0;7;8;12;17;23} هي مجموعة منتهية مكونة من 8 عناصر اذن cardE=8

1.2 تقاطع مجموعتين منتهيتين

1.2.1 مثال

E={1;2;3;4;5;7} و F={-3;-2;0;1;5;7;10;13} و G={-2;10;15;20}
العناصر المشتركة بين المجموعتين E و F هي 1 ; 5 ; 7, نقول ان المجموعة {1;5;7} هي تقاطع المجموعتين E و F, ونكتب E∩F={1;5;7}
لا يوجد اي عنصر مشترك بين المجموعتين E و G, نقول ان المجموعتين E و G منفصلتان ونكتب ∅=E∩G

1.2.1 تعريف

تقاطع مجموعتين منتهيتين E و F , ونكتب E∩F هي محموعة ة العناصر المشتركة بينهما
وبعبارة اخرى
E∩F = {x / x∈E و x∈F}

1.3 اتحاد مجموعتين منتهيتين

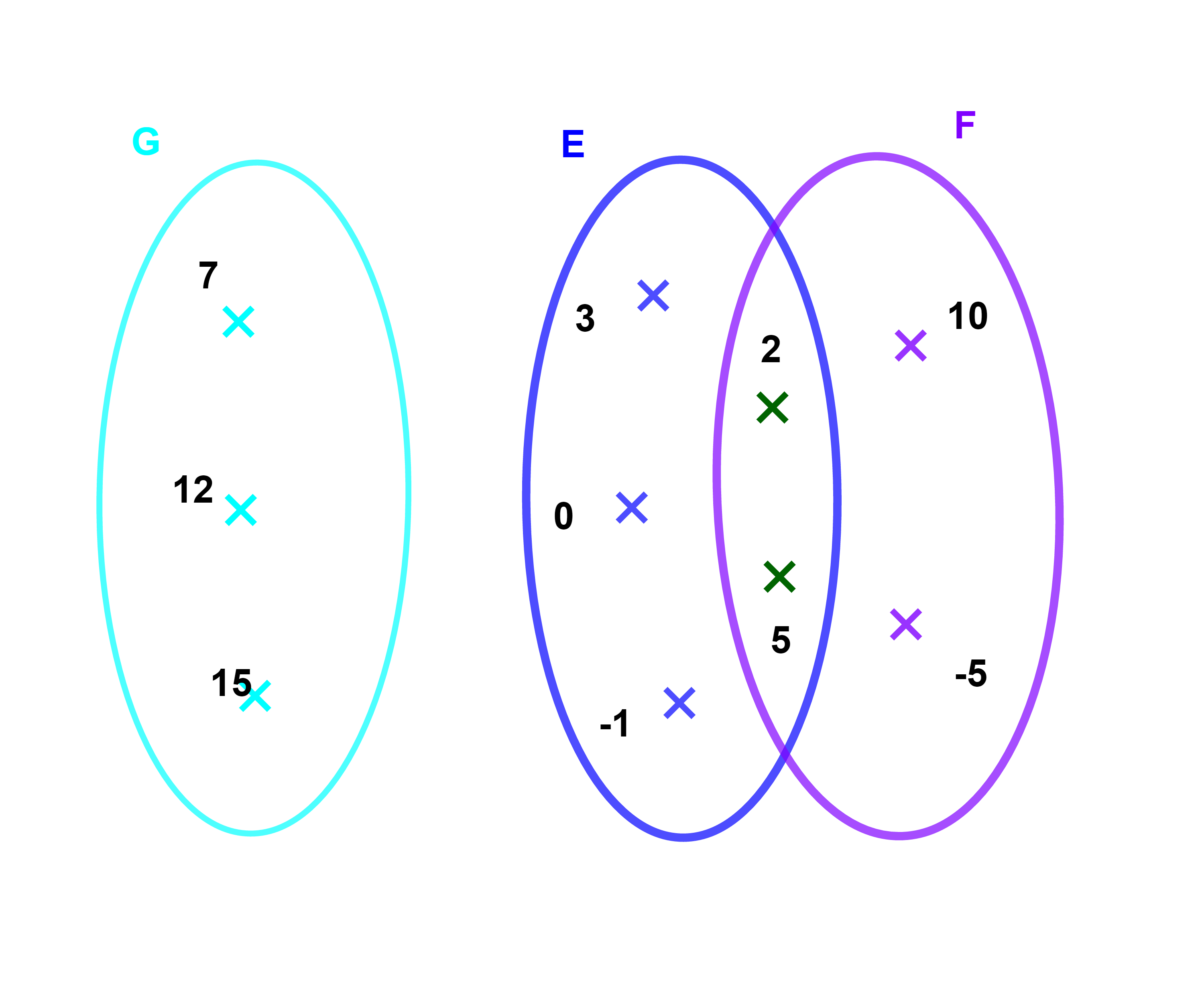
1.3.1 مثال

E={-1; 0; 2; 3; 5} ; F={-5; 2; 5; 10} و G={7; 12; 15 }
المجموعة المكونة من عناصر E و F
هي {-5; -1; 0; 2; 3; 5;10 } وتسمى اتحاد E و F ونكتب E∪F

1.3.2 تعريف

اتحاد مجموعتين منتهيتين E و F , ونكتب E∪F هي المجموعة المكونة من عناصر E و F
وبعبارة اخرى
E∪F = {x / x∈E او x∈F}

1.3.3 خاصيات

E و F مجموعتان منتهيتان
اذا كان ∅ =E∩F فان card(E∪F)=cardE+cardF
اذا كان ∅≠E∩F فان
card(E∪F)=cardE+cardF-cardE∩F

2- المبدا الاساسي للتعداد و شجرة الاختيار

2.1 المبدا الاساسي للتعداد

2.1.1 خاصيات

في تجربة مكونة من k مرحلة , اذا كانت المرحلة الاولى تنفذ من n₁ طريقة مختلفة و كانت المرحلة الثانية تنفذ من n₂ طريقة مختلفة
وهكذا الى المرحلة k التي تنفذ من n_k طريقة مختلفة فان جميع هذه المراحل المتتالية يمكن ان تنفذ ب n₁×n₂×...×n_k طريقة مختلفة
وهذا ما يطلق عليه ب المبدا الاساسي للتعداد او مبدا الجداء

2.1.2 مثال 1

اذا كان لشخص ثلاث اقمصة وسروالين وزوج حدائين فان هذا الشخص له
ثلاث اختيارات لارتداء قميص واربع اختيارات للبس سروال وخيارين للبس زوج حداء
وحسب المبدا الاساسي للتعداد فان عدد جميع الاختيارات لهذا الشخص هو 3×4×2 = 24

2.2 شجرة الاحتيار

2.1.1 مثال

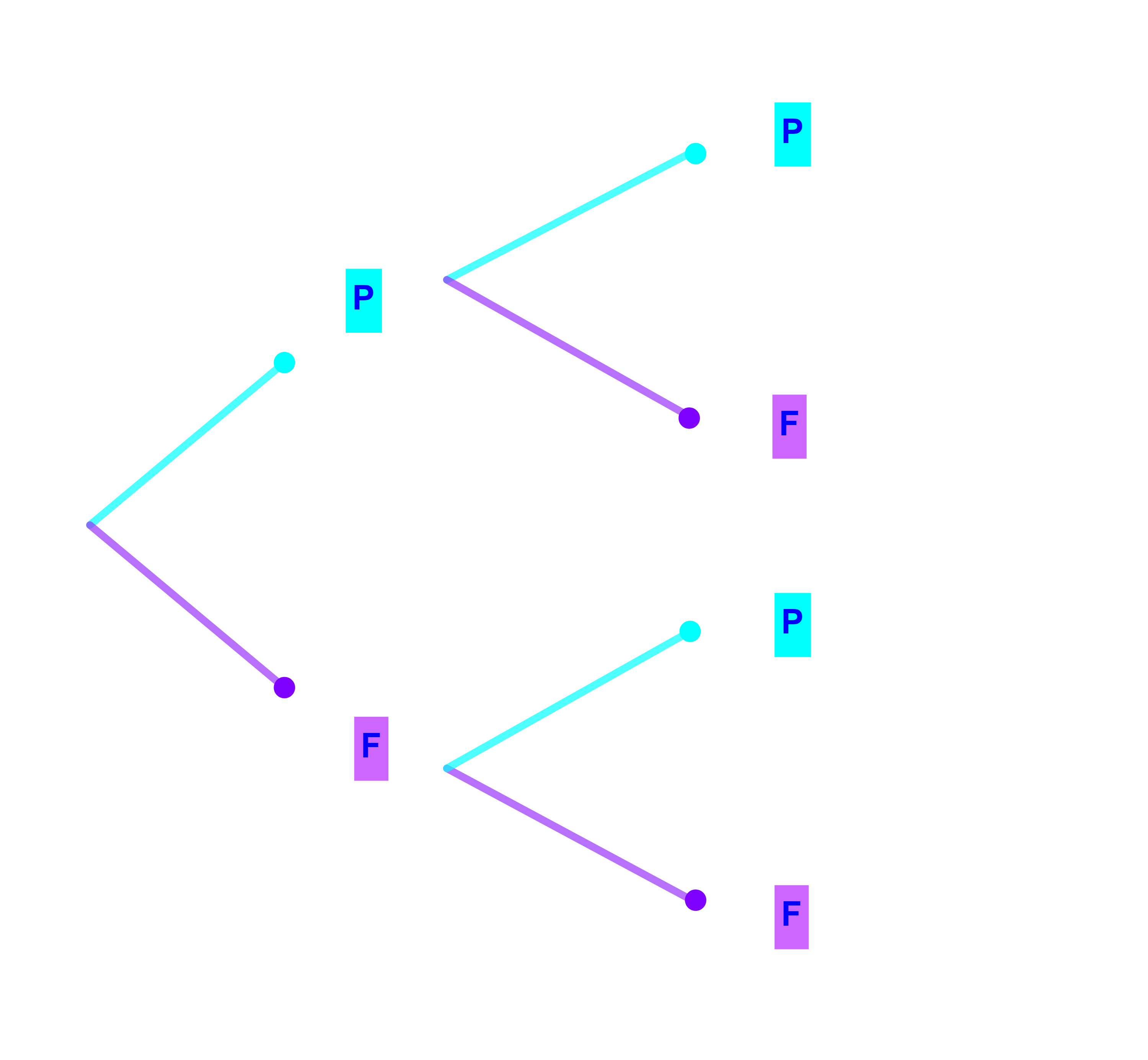
1) عندما نرمي قطعة نقدية في الهواء فانها ستقع اما على الوجه F, واما على الظهر P, اذن توجد امكانيتين هما : P او F.
2) واذا رميت قطعة نقدية مرتين على التوالي فان عدد الامكانيات هو 2×2=4, FF; FP; PF et PP

2.2.2 مثال 3

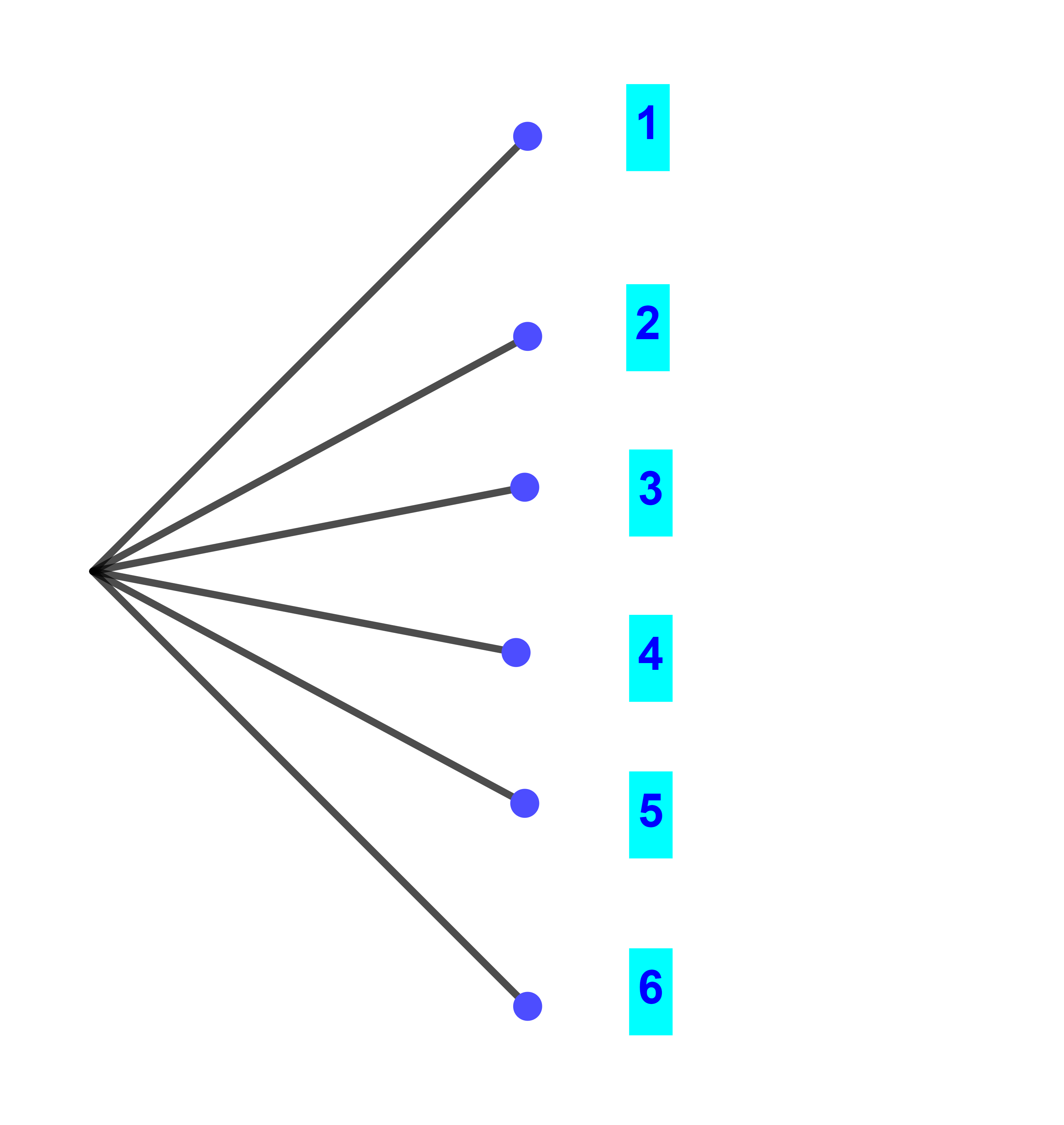
1) عندما نرمي نردا على طاولة فانه يترتب عن ذلك ظهور اما الرقم 1 او الرقم 2 او الرقم 3 او الرقم 4 او الرقم 5 او الرقم 6 اذن توجد 6 امكانيات
2) واذا رمينا نردا مرتين على التوالي فان عدد النتائج الممكنة هو 6×6=36 .

تمرين 1

اذا رمينا نردا ثلاث مرات على التوالي ما هو عدد النتائج الممكنة ?

تمرين 2

1) كم عدد ممكن تكوينه من رقمين من الارقام التالية 1 ; 2 ; 3 ; 4 ; 5 ?
2) كم عدد ممكن تكوينه من ثلاث ارقام مختلفة من الارقام التالية 1 ; 2 ; 3 ; 4 ; 5 ?