Fonctions Exponentielles (3)
1.3 Etude de la fonction exp
1.3.1 Domaine de définition de exp
La fonction exp est définie de IR vers IR+*
Dexp =IR.
1.3.2 Limites et branches infinies
Le plan est rapporté à un repère orthonormé
(O;i→;j→). Soit (C) la courbe représentative de la fonction exp.
lim +∞ | ex = +∞ |
lim - ∞ | ex = 0 |
et cela signifie que l'axe des abscisses est une asymptote à la courbe (C) au voisinage de -∞.
| lim+∞ | ex | = +∞ |
| x |
et cela signifie que la courbe (C) admet une branche parabolique de direction l'axe des ordonnées.
1.3.3 Dérivé de exp
(∀x∈IR): ex > 0.
La fonction exp est dérivable sur IR
et (∀x∈IR): (ex)'= ex.
Démonstration
On a: (∀x∈IR): (ex)'=(ln-1)'(x)
| (ln-1)'(x)= | 1 | = | 1 |
| ln'(ln-1(x)) | ln(ln-1(x)) |
ainsi (ex)' = ex.
Donc la fonction exp est strictement croissante sur IR.
Tableau de variations
| x | -∞ | +∞ | ||
| f | 0 | ↗ | +∞ |
1.3.4 Courbe représentative
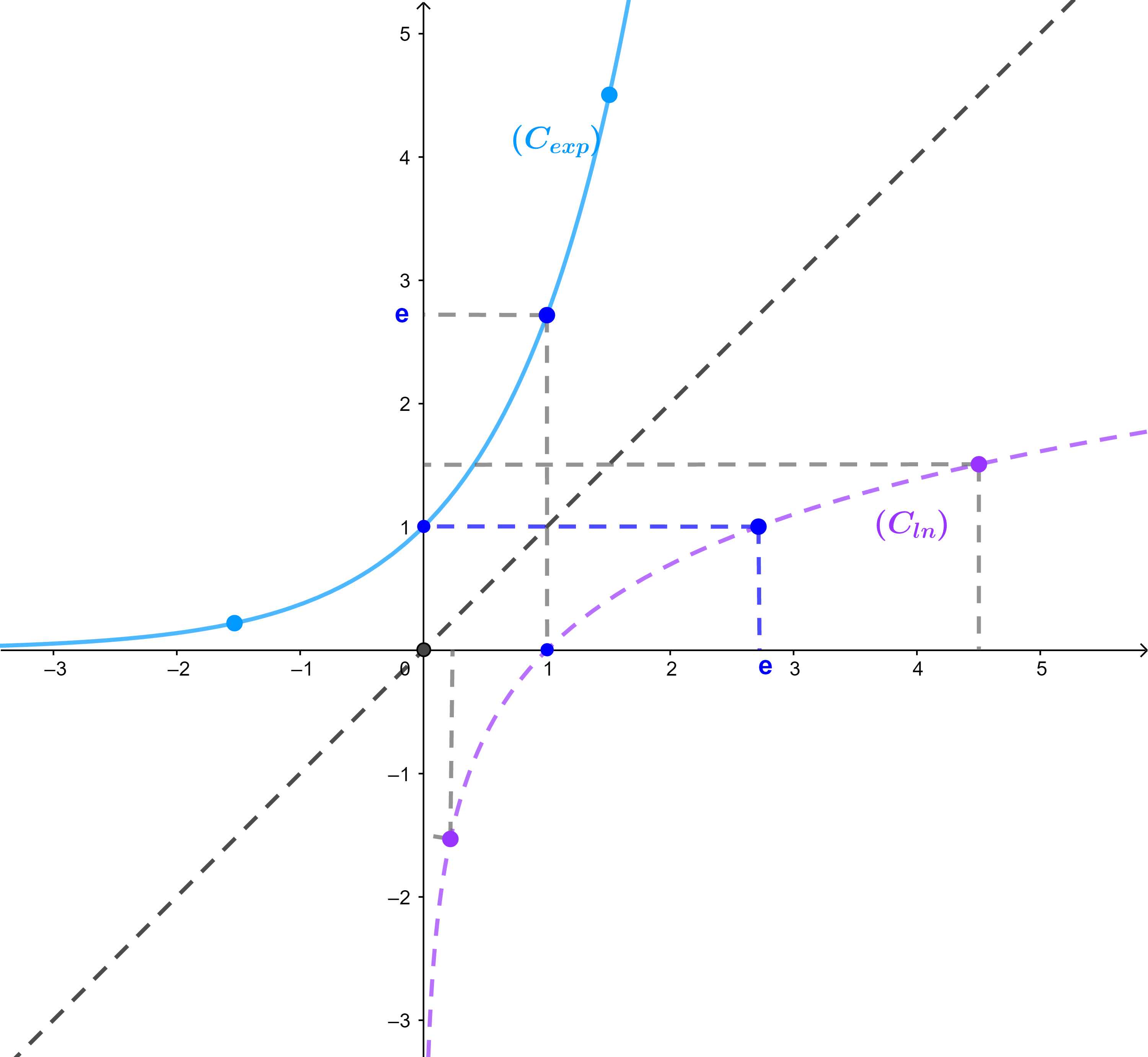
La courbe de la fonction exp est symétrique par rapport à la droite (D): y=x.
1.3.5 Limites usuelles
lim +∞ |
ex = +∞ | lim -∞ |
ex = 0 |
lim 0 |
ex-1 | = 1 |
| x |
lim -∞ |
xex= 0 | lim -∞ |
xnex=0 avec n∈Z |
lim +∞ |
ex | = +∞ | lim +∞ |
ex | = +∞ avec n∈ℤ | |
| x | xn |
Exercice 1 tp
Calculer la limite suivante
lim +∞ |
ex-lnx |
Correction
lim +∞ |
ex - lnx |
La substitution de la limite dans l'expression de f conduit à une forme indéfinie +∞-∞. Elle doit donc être effectuée d'une autre manière.
| ex-lnx= x( | ex | - | lnx | ) |
| x | x |
En utilisant les deux limites usuelles suivantes
lim +∞ | ex | = +∞ | lim +∞ | lnx | = 0 | |
| x | x |
on obtient
lim +∞ |
ex - lnx | = +∞(+∞-0) = +∞ |