دراسة دوال عددية (1)
1- تذكير
1.1 الرتابة
| I دالة تزايدية على f ⇔ ∀x∈I: f'(x) ≥ 0 |
| I دالة تناقصية على f ⇔ ∀x∈I: f'(x) ≤ 0 |
1.2 الفروع اللانهائية والمقاربات
1.2.1 تعريف :
لتكن f دالة عددية لمتغير حقيقي x
و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O ;i→;j→)
اذا آلت احداتيات نقطة من المنحنى (C)
الى ما لانهاية فان المنحنى (C) يقبل فرعا لانهائيا
يعني اذا كان x→±∞
او f(x)→±∞.
1.2.2 مقارب مواز لمحور الاراتيب
اذا كانت lima- f(x) = +∞ او lima- f(x) = -∞
او lima+ f(x) = +∞ او lima+ f(x) = -∞
فان المستقيم ذو المعادلة x = a هو مقارب
للمنحنى (C).
1.2.3 مقارب مواز لمحور الافاصيل
اذا كانت lim-∞f(x)=b او lim+∞f(x)=b فان المستقيم ذو المعادلة y=b مقارب للمنحنى (C) بجوار -∞ او من +∞
مثال
لتكن f دالة عددية معرفة بما يلي
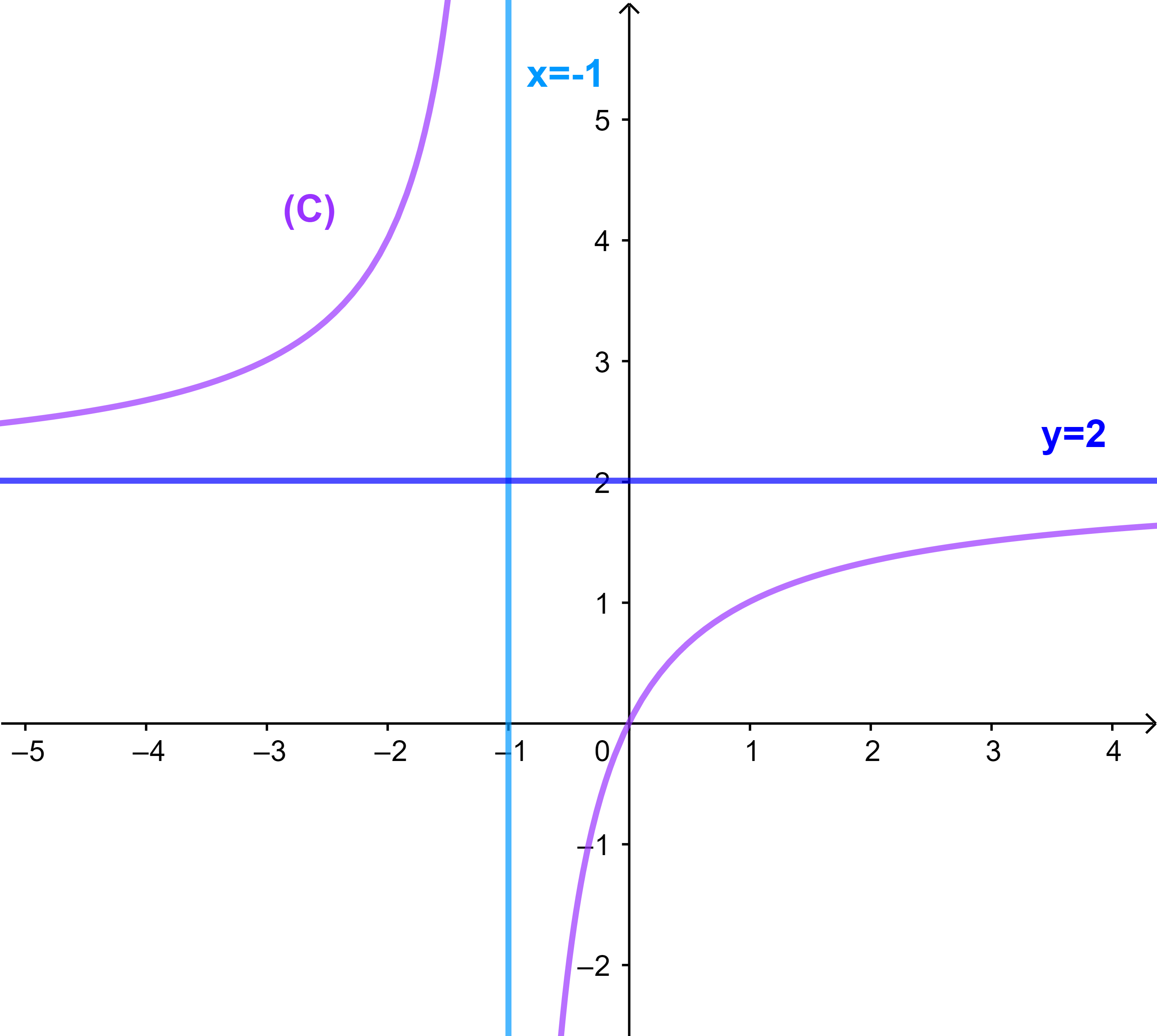
| f(x)= | 2x |
| x+1 |
1) لدينا : lim+∞f(x)=2 اذن المستقيم
(D):y=2 هو مقارب للمنحنى (C) بجوار +∞
2) lim-1+ f(x) = +∞ اذن المستقيم (D): x=-1 هو مقارب للمنحنى (C) على يمين 1
3) lim-1- f(x) = +∞ اذن المستقيم (D): x=-1 هو مقارب للمنحنى (C) على يسار 1
1.2.4 المقارب المائل
في هذه القفرة الدالة f تقبل تهاية غير منتهية عند
±∞
اذا كانت lim+∞f(x)-(ax+b)= 0
او (lim-∞f(x)-(ax+b)=0) حيث a∈IR*
و b∈IR فان المستقيم
(D) الذي معادلته y=ax+b
مقارب مائل
للمنحنى (C) بجوار +∞
او (-∞) .
خاصية :
لتكن f دالة عددية و (C) المنحنى الممثل لها , المستقيم ذو المعادلة y=ax+b مقارب
مائل للمنحنى (C) بجوار
+∞ او -∞ اذا وفقط اذا وجدت دالة عددية
h بحيث f(x)=ax+b+h(x)
و lim+∞h(x)=0
او (lim-∞h(x)=0)
مثال
لتكن f دالة عددية معرفة كما يلي
| f(x)=2x+1+ | 1 |
| x |
| lim±∞f(x)-(2x+1)=lim±∞ | 1 | =0 |
| x |
اذن lim±∞f(x)-(2x+1)=0
ومنه فان المستقيم ذو المعادلة y=2x+1 مقارب مائل للمنحنى (C) بجوار +∞ او -∞
خاصية :
اذا كانت lim±∞f(x)=±∞ و
| lim±∞ | f(x) | = a ; lim±∞f(x)-ax=b |
| x |
فان المستقيم الذي معادلته y = ax+b مقارب للمنحنى Cf بجوار +∞ او -∞
تمرين
لتكن f دالة عددية معرفة كما يلي
| f(x)= | x²-4x+5 |
| x-2 |
1) حدد Df.
2) حدد مقاربات المنحنى (C)
1.4 تقعر دالة ونقط انعطاف
خاصيات
اذا كان ∀x∈I : f"(x)≥0
فان المنحنى
Cf محدب
اذا كان ∀x∈I : f"(x)≤0
فان المنحنى
Cf مفعر
اذا كان ∀x∈I : f"(a)=0
و
f"
تغير اشارتها في a
فان
A(a;f(a)) نقطة انعطاف للمنحنى.