Dérivation et représentation (13)
Exercice 1 tp
On considère une fonction f définie par
| f(x) = x - | x |
| x²-1 |
et (C) sa courbe dans un repère
orthonormé (O ; i→ ; j→).
1) Montrer que f est impaire
et déterminer les limites de f en +∞ et à droite à 1
2) Déterminer les asymptotes de (C)
3) (a) Etudier la monotonie de f et tracer son tableau de variations sur D
(b) Déterminer l'équation de la tangente à (C) au point O
4) (a) Tracer la courbe (C)
(b) Résoudre graphiquement
l'inéquation f(x) ≥ 0
5) Soit g la restriction de la fonction f sur l'intervalle I=[0 ; 1[
(a) Montrer que la fonction g admet une fonction réciproque g-1 définie dans un intervalle J qui doit être spécifié
(b) Montrer que g-1 est dérivable au point 0 et calculer (g-1)'(0)
(c) Déduire l'équation de la tangente à (Cg-1) au point O
Correction
1) D={x∈IR/x²-1≠0}
=]-∞;-1[∪]-1;1[∪]1;+∞[
le domaine D est centrer en 0 donc
∀x∈D, (-x)∈D , soitx∈D
| f(-x) = -x - | -x | = -(x - | x | ) |
| x²-1 | x²-1 |
Donc f(-x) = - f(x) ainsi f est impaire
Il suffit donc d'étudier f sur [0;1[∪]1;+∞[
| x | 0 | 1 | +∞ | ||
| x²-1 | - | || | + |
lim 1+ | x | = | 1 | =+∞ |
| x²-1 | 0+ |
donc
lim 1+ |
f(x) = 1-∞= - ∞ |
lim +∞ | x | = | lim +∞ | x | = | lim +∞ | 1 | =0 |
| x²-1 | x² | x |
| donc | lim +∞ |
f(x) = +∞ - 0= + ∞ |
| 2) | lim 1+ |
f(x) = - ∞ |
donc la droite d'équation x=1 est une asymptote de (C)
Puisque f est impaire alors la droite d'équation x=-1 est une asymptote de (C)
lim +∞ | f(x)-x = | lim +∞ | x | = 0 |
| x²-1 |
donc la droite (D) d'équation y=x est une asymptote de (C) au voisinage de +∞
et puisque f est impaire alors (D) est aussi une asymptote de (C) au voisinage de -∞
3) (a) f est une fonction rationnelle, donc dérivable sur D
Soit x∈D
| f '(x)= 1 - | (x²-1)-2x² | = 1 + | x²+1 |
| (x²-1)² | (x²-1)² |
Donc ∀x∈D
| f '(x)= 1 + | x²+1 |
| (x²-1)² |
x²+1> 0 et (x²-1)²>0 donc (∀x∈D): f '(x)>0
ainsi f est strictement croissante
sur des intervalles [0;1[ et ]1;+∞[
f est impaire donc f est également strictement croissante sur des intervalles ]-∞;-1[ et ]-1;0]
| x | -∞ | -1 | 1 | +∞ | |||||||
| f' | + | + | + | ||||||||
| f | -∞ |
↗ |
+∞ | -∞ |
↗ |
+∞ | -∞ |
↗ |
+∞ | ||
(b) f est dérivable sur D et on a 0∈D donc f est dérivable au point 0 ainsi la courbe (C) admet une tangente (T1) au point O d'équation
y = f'(0)(x-0)+f(0)
On a f(0)=0
| et f '(0)= 1 + | 0²+1 | = 2 |
| (0²-1)² |
Alors (T1): y=2x
4) (a) La courbe (C)
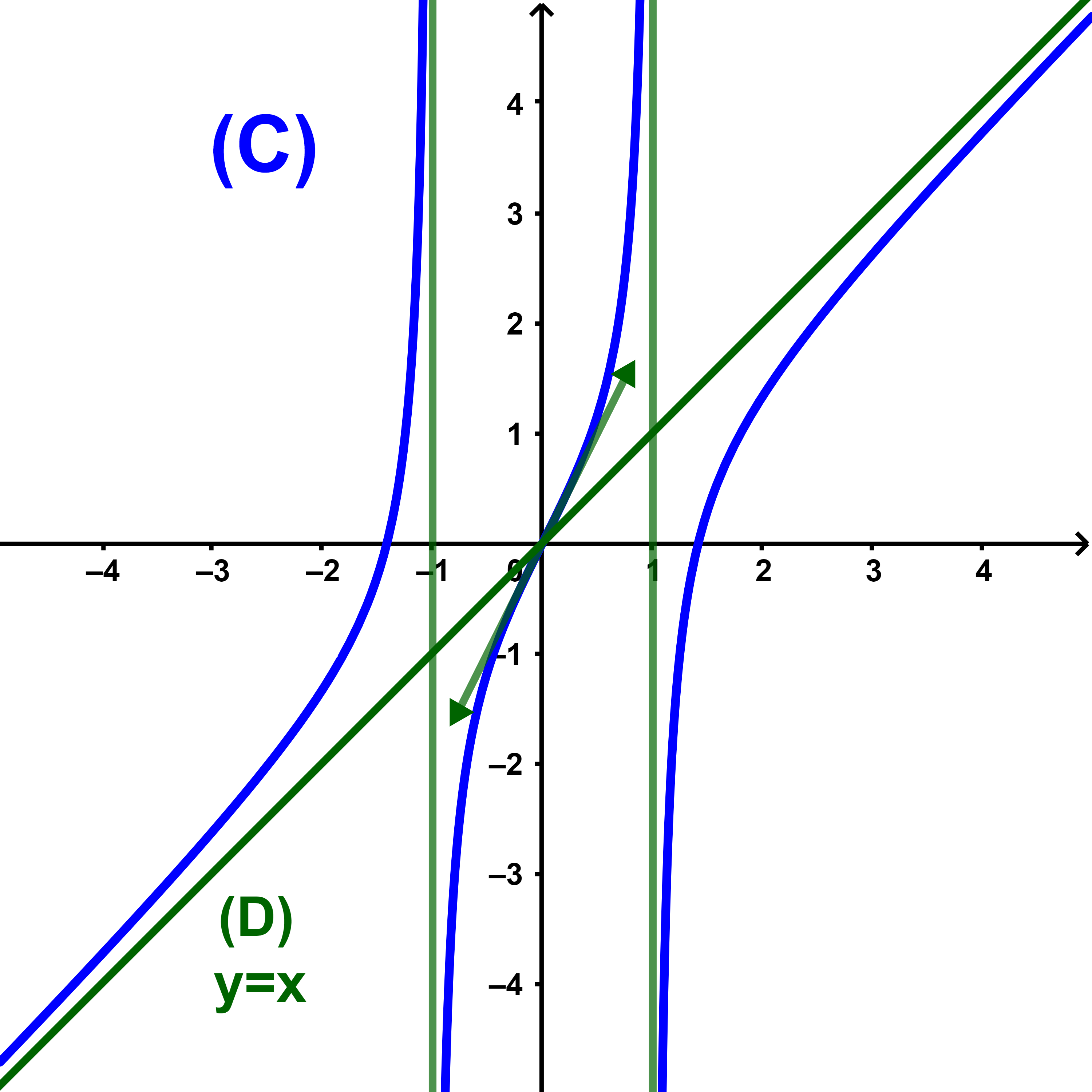
(b) (C) coupe l'axe des abscisses en trois points d'abscisses respectives a tel que
-2<a<-1 , b=0
et c tel que 1<c<2
l'ensemble de solutions de l'inéquation f(x)≥0 est l'ensemble des abscisses des points de la courbe (C) situés au-dessus de l'axe des abscisses
donc S=[a;-1[∪[0;1[∪[c;+∞[
5) Soit g la restriction de la fonction f sur l'intervalle I=[0 ; 1[
(a) la fonction f est continue sur D et I⊂D donc f est continue sur I ainsi g est continue sur I
de plus f est strictement croissante sur I donc g est également strictement croissante sur I
alors la fonction g admet une fonction réciproque g-1 définie dans l'intervalle J=f(I)
| J = f([0 ; 1[) = [f(0) ; | lim 1- | f(x)[ |
Donc J = [0 ; +∞[
(b) f est dérivable au point 0 et f '(0)=2≠0 donc g est également dérivabe au point 0 et g'(0)=2≠0
ainsi g-1 est dérivable au point g(0)=0
| et (g-1)'(0) = | 1 | |
| g'(0) |
| Donc (g-1)'(0) = | 1 | |
| 2 |
(c) Equation de la tangente à (Cg-1) au point O
g-1 est dérivable au point 0
donc la courbe (Cg-1) admet une tangente (T2) au point O d'équation
y = (g-1)'(0)(x-0)+g-1(0)
On a g-1(0)=0
| et (g-1)'(0) = | 1 |
| 2 |
| Donc (T2): y = | 1 | x |
| 2 |