Dérivation et représentation (16)
Exercice 1 tp
On considère une fonction f définie par
| f(x) = x - | 2 |
| √(x-1) |
et (C) sa courbe dans un repère orthonormé.
1) Calculer les limites de f en +∞ et en 1
2) Déterminer les asymptotes de (C)
2) Résoudre dans IR l'équation (E)
(x-1)√(x-1)+1=0
3) Calculer f'(x) puis étudier son signe et tracer le tableau de variations de f
4) Soit g la restriction de f sur I=]1 ; +∞[
Montrer que g admet une fonction réciproque g
5) Tracer les courbes (Cf) et (Cg-1) dans le même repère
et déduire graphiquement le signe de f
Correction
1) D={x∈IR/ x-1≥0 et √(x-1)≠0}
=]1;+∞[
Limite de f en +∞
lim +∞ |
x-1 = +∞ ⇒ | lim +∞ |
√(x-1) = +∞ |
| ⇒ | lim +∞ | 2 | = 0 |
| √(x-1) |
+∞ + 0 = +∞
| donc | lim +∞ | f(x) | = +∞ |
Limite de f en 1+
| x | -∞ | 1 | +∞ | ||
| x-1 | - | 0 | + |
lim 1+ | 1 | = | 1 | = +∞ |
| x-1 | 0+ |
| ⇒ | lim 1+ | 1 | = +∞ |
| √(x-1) |
lim 1+ | f(x) = | lim 1+ |
x+ | 2 |
| √(x-1) |
| Donc | lim 1+ | f(x) = 1+∞=+∞ |
ainsi (C) admet une asymptote d'équation x=1
lim +∞ |
f(x) - x = | lim +∞ | 2 |
| √(x-1) |
| donc | lim +∞ | f(x)-x = 0 |
Ainsi (C) admet une asymptote oblique d'équation y=x
2) On résout dans D l'équation
(x-1)√(x-1)+1=0
x>1 ⇒ x-1>0 ⇒ √(x-1)>0
donc ∀x>1, (x-1)√(x-1)+1>0
ainsi S=∅
3) x→x-1 est strictement positive et dérivable sur D
donc x→ √(x-1) est dérivable sur D
Ainsi
| x→ | 2 |
| √(x-1) |
est dérivable sur D
Puisque x→x est dérivable sur IR, et en particulier sur D alors f est continue et dérivable sur D . Soit x∈D
| f '(x) = 1 +2 | (√(x-1))' |
| (√(x-1))² |
| = 1 + | 2 |
| (x-1)2√(x-1) |
| ainsi f '(x)=1 + | 1 |
| (x-1)√(x-1) |
On a x>1 ou encore x-1>0 et √(x-1)>0
donc (∀x∈D) on a f '(x)>0
alors f est strictement croissante sur D
Tableau de variations
| x | 1 | +∞ | ||
| f '(x) | + | |||
| f | -∞ | ↗ | +∞ |
4) f est continue et strictement croissante sur I=]1 ; +∞[ donc g est continue et strictement croissante sur I
Ainsi g admet une fonction réciproque g-1 définie de J = f(I) vers I
| J = ] | lim 1+ | f(x) ; | lim +∞ | f(x)[ = ]-∞ ; +∞[ |
g(2) = 0 donc g-1(0) = 2
f est dérivable au point 2 donc g est dérivable au point 2
g '(2) = f '(2) = 2 ≠ 0 donc g-1 est dérivable au point g(2)=0 ainsi
| (g-1) '(0) = | 1 | = | 1 |
| g'(2) | 2 |
5) Les courbes (C)
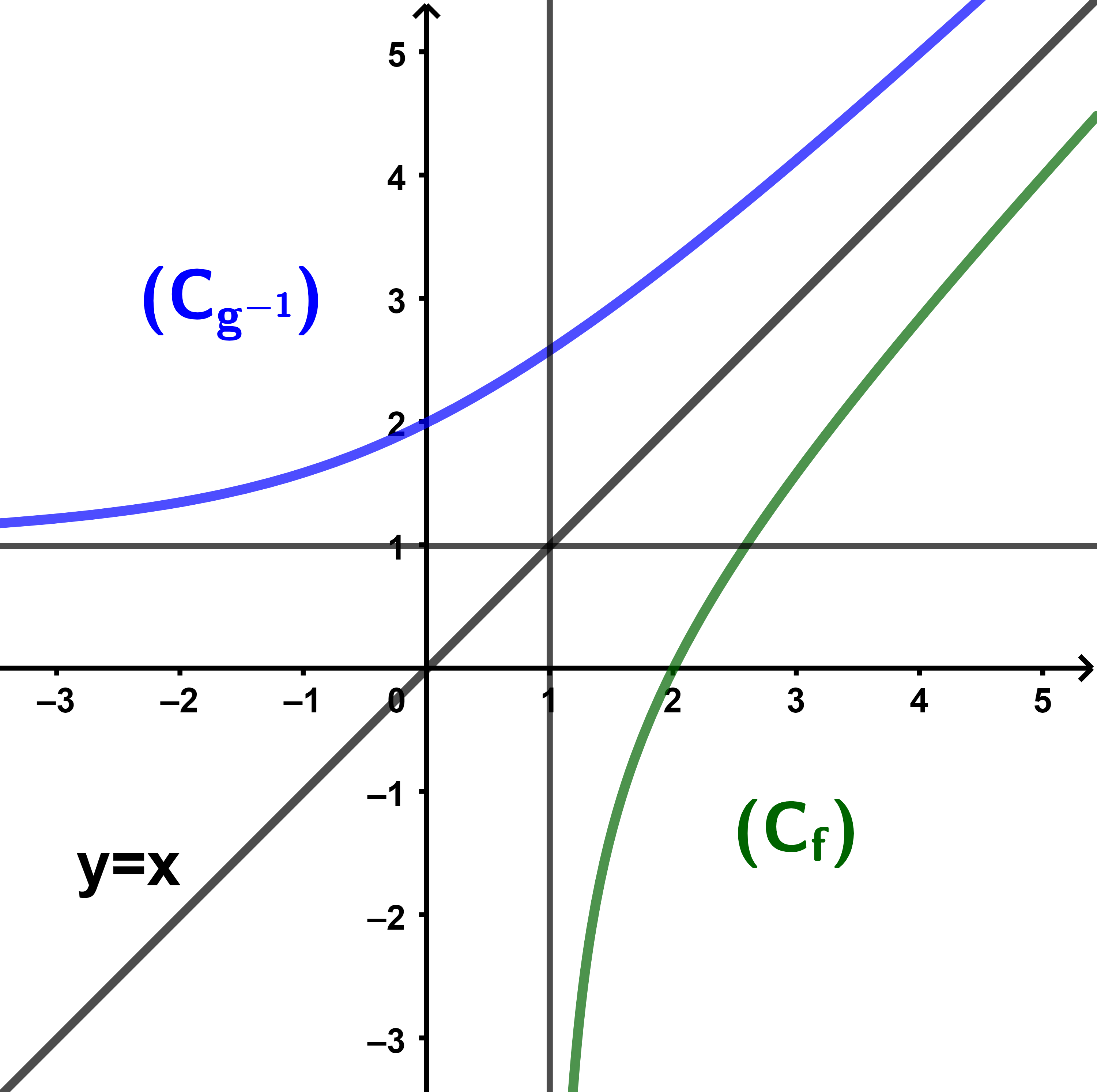
5) La courbe (C) coupe l'axe des abscisses en un seul point A(2;0)
La partie de la courbe (C) au dessus de l'axe des abscisses est l'ensemble des points, leurs abscisses appartiennent à l'intervalle I=[2;+∞[
La partie de la courbe (C) au dessous de l'axe des abscisses est l'ensemble des points, leurs abscisses appartiennent à l'intervalle J=]1;2]
Donc f est postive sur l'intervalle I=[2;+∞[
et f est négative sur l'intervalle J=]1;2]
| { | f(x) ≥ 0 | si x ≥ 2 |
| f(x) ≤ 0 | si 1 < x ≤ 2 |