الجداء المتجهي (1)
1- توجيه الفضاء الجداء المتجهي
1.1 توجيه الفضاء
1.1.1 تقديم
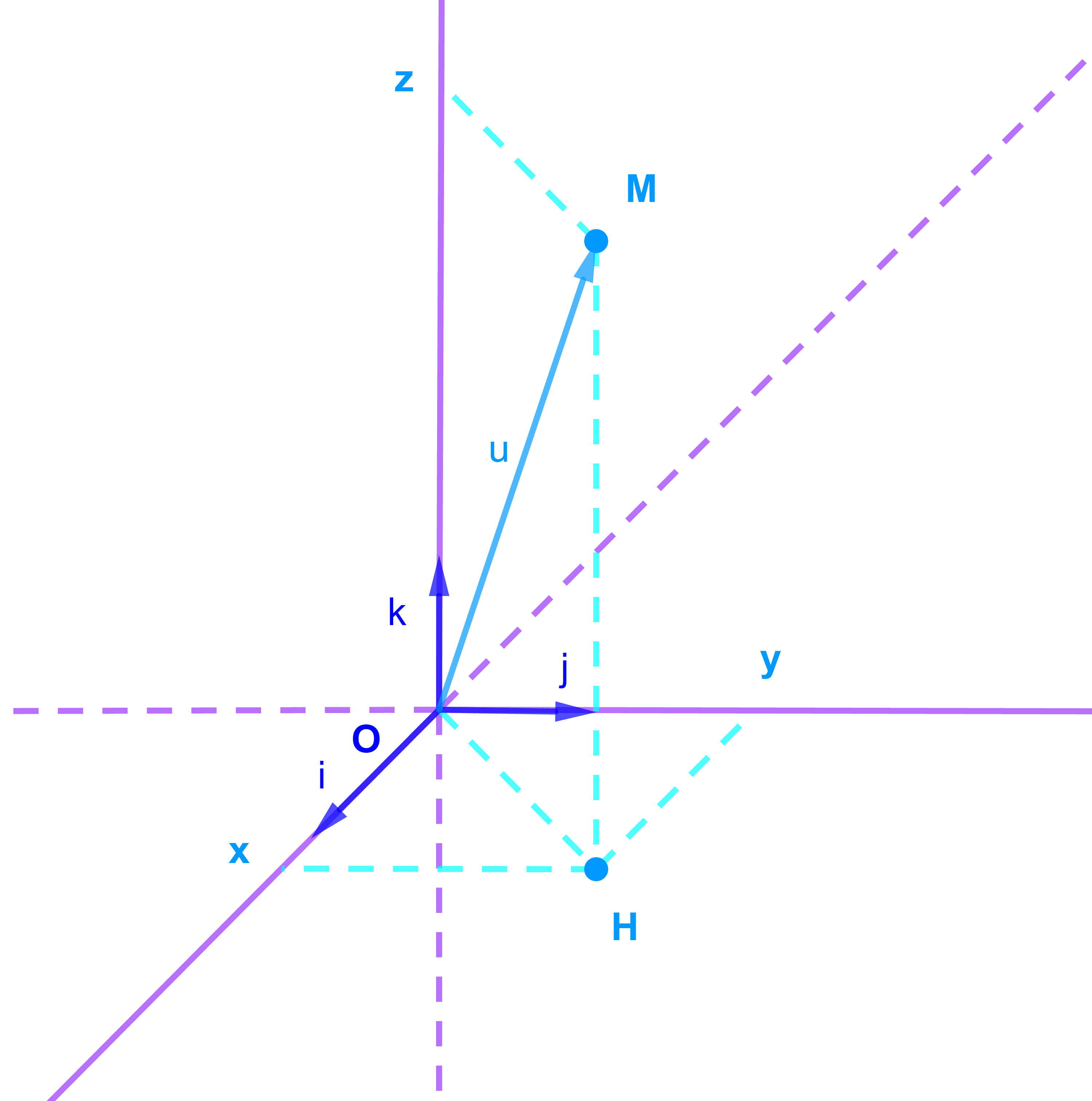
i→ و j→ متجهتان متعامدتان منظمهما يساوي 1
في الفضاء الاعتيادي
هناك امكانيتان لاضافة متجهة ثالثة لهما من اجل الحصول على اساس ممتعامد ممنظم في
V3
لذلك هناك اساسان
B(i→;j→;k→)
و B'(i→;j→;-k→)
رجل امبير , هو رجل خيالي راسه في K;
وقدماه في O وينظر الى النقطة I, (OIJK) رباعي الوجوه,
OI→=i→; OJ→=j→
و OK→=k→
اذا كانت الزاوية (i→;j→) موجبة,
فان الاساس B مباشر وكل مثلوث من متجهات غير مستوائية (u→;v→;w→)
موجهة
1.1.2 خاصية
(i→;j→;k→) اساس مباشر و O نقطة من الفضاء
المربوع (O;i→;j→;k→)
معلم متعامد ممنظم مباشر
وبالتالي الفضاء موجه.
1.1.3 امثلة
(O;i→;j→;k→)
معلم متعامد ممنظم مباشر
(i→;j→;k→)
اساس مباشر
(j→;i→;k→)
اساس غير مباشر
(j→;k→;i→)
اساس مباشر
1.2 الجداء المتجهي
1.2.1 تعريف:
الجداء المتجهي لمتجهتين
u→ و v→ في الفضاء
V3 ونكتب u→∧v→,
هو متجهة معرفة بما يلي
(1) اذا كانت u→ و v→ مستقيميتين فان :
u→ ∧ v→ = O→
(2) اذا كانت u→ و v→
غير مستقيميتين فان :
(a) (u→ ∧ v→) ⊥ u→
و (u→ ∧ v→) ⊥ v→
(b) الاساس (u→ ; v→ ; u→ ∧ v→) مباشر
(c) ||u→ ∧ v→||
=||u→||×||v→||sin(u→;v→)
1.2.2 نتائج
مساحة المثلث (ABC) هي :
| S = | 1 | ||AB→∧AC→|| |
| 2 | ||
| = | 1 | AB×AC×sin(AB→;AC→) |
| 2 |
1.2.3 امثلة
i→∧j→=k→
k→∧j→=-i→
k→∧i→=j→
i→∧i→=j→∧j→=k→∧k→=O→
1.2.4 التخالفية والتماثلية الخطية
لتكن u→ و v→ و w→
متجهات القضاء V3 و k عدد حقيقي غير منعدم
التخالفية
u→∧v→=- v→∧u→
تنائية الخطية
u→∧(v→+w→)=u→ ∧ v→ + u→ ∧ w→
و ku→∧v→ = u→∧(kv→) = (ku→)∧v→
ملاحظة:
التجميعية غير محققة على العموم
اي u→∧(v→∧w→)≠(u→∧v→)∧w→
2- الصيغة التحليلية للجداء المتجهي
2.1 احداتيات الجداء المتجهي لمتجهتين
2.1.1 خاصية
الفضاء منسوب الى معلم متعامد ممنظم مباشر
(O;i→;j→;k→)
u→(x;y;z) ; v→(x';y';z')
∈V3
u→ ∧v→=
(yz'-zy')i→-(xz'-zx')j→+(xy'-yx')k→
برهان
u→ ∧ v→=
(xi→+yj→+zk→)∧(x'i→+y'j→+z'k→)
=xx'i→∧i→+xy'i→∧j→+xz'i→∧k→
+yx'j→∧i→+yy'j→∧j→+yz'j→∧k→
+zx'k→∧i→+zy'k→∧j→+zz'k→∧k→
=xx'O→+xy'k→-xz'j→
-yx'k→+yy'O→+yz'i→
+zx'j→-zy'i→+zz'O→
=(yz'-zy')i→-(xz'-zx')j→+(xy'-yx')k→
اذن
u→∧v→=
(yz'-zy')i→-(xz'-zx')j→+(xy'-tx')k→
ملاحظة:
يمكن استعمال جداول المحددات لتذكر الصيغة
| u→∧v→= | i→ | x | x' | |
|---|---|---|---|---|
| j→ | y | y' | ||
| k→ | z | z' |
| = | y | y' | i→ | ||
|---|---|---|---|---|---|
| z | z' | ||||
| - | x | x' | j→ | ||
| z | z' | ||||
| + | x | x' | k→ | ||
| y | y' | ||||
| =(yz'-zy')i→-(xz'-zx')j→+(xy'-yx')k→ | |||||
2.1.2 مثال
لتكن u→(2;1;0) و v→(1,2,4) متجهتين.
نحدد u→∧v→.
| u→∧v→ = | i→ | 2 | 1 | |
| j→ | 1 | 2 | ||
| k→ | 0 | 4 |
| = | 1 | 2 | i→ | - | 2 | 1 | j→ | |
| 0 | 4 | 0 | 4 | |||||
| + | 2 | 1 | k→ |
| 1 | 2 | ||
=(1x4-0x2)i→-(2x4-0x1)j→+(2x2-1x1)k→
=4i→-8j→+3k→
ومنه فان u→∧v→(4;-8;3).
2.1.3 مثال
لتكن u→(5;-2;1) و v→(2,7,-4) متجهتين من V3.
| u→∧v→ = | i→ | 5 | 2 | |
| j→ | -2 | 7 | ||
| k→ | 1 | -4 |
=((-2)x(-4)-1x7)i→ - (5x(-4)-1x2)j→
+ (5x7-(-2)x2)k→
= i→ + 22j→ + 39k→
ومنه فان u→∧v→(1 ; 22 ; 39).
2.1.4 خاصية 1
ثلاث نقط غير مستقيمية A و B و C من الفضاء تحدد مستوى متجهته المنظمية AB→∧AC→.
2.1.5 خاصية 2
لتكن A و B و C ثلاث نقط من الفضاء.
AB→∧AC→=0→ ⇔ A و B و C مستقيمية.
2.2 مسافة نقطة عن مستقيم
2.2.1 خاصية
B نقطة من الفضاء و D(A;u→) مستقيم.
لدينا AB→ ∧ u→=(AH→ + HB→)∧ u→
= HB→ ∧ u→
لان AH→ و u→ مستقيميتان
اذن
| HB = | || AB→ ∧ u→ || |
|---|---|
| || u→ || |
2.2.2 امثلة
D(A;u→) مستقيم حيث u→(2;2;-1) و A(2;0;1). نعتبر نقطة B(-2;1;2) من الفضاء.
لدينا AB→∧u→=-3i→-2j→-10k→ و ||u→||=3
اذن
| d(B;(D))= | √(9+4+100) | = | √113 |
| 3 | 3 |