Droite dans le plan (12)
3.2 Application
Programmation linéaire
Exemlpe
Une communauté construient deux types de tapis T1 et T2. Le jour utilisent la machine et la nuit travaille à la main. Elles ont réservé un budget de 5000 Dh pour la matière première et 15000 Dh pour la main d'oeuvre. Chaque tapis rapportrait un gain de 750 Dh.
Sachant qu'un tapis de type T1 demande 2000dh pour la matière première et 3000 Dh pour la main d'oeuvre.
Alors pour le tapis T2, 1000 Dh pour la matière première et 4000 Dh pour la main d'oeuvre.
Combien de tapis de chaque type devraient elles fabriquer pour obtenir le maximum de profils possible ?
Correction
On désigne par x et y les nombres respectifs des tapis T1 et T2.
| Type | T1 | T2 | Total |
| Matière première | 2000/1 | 1000/1 | 5000 |
| Main d'oeuvre | 3000/1 | 4000/1 | 15000 |
La matière première est représentée par l'inéquation
2000x+1000y≤5000
et la main d'oeuvre est représentée par l'inéquation
3000x+4000y≤15000.
Et évidemment x>0 et y>0 des entiers naturels.
Le couple (x;y) vérifie le système
| { | 2000x + 1000y ≤ 5000 |
| 3000x + 4000y ≤ 15000 | |
| x>0 et y>0 |
Signifie
| (S) : { | 2x + y ≤ 5 |
| 3x + 4y ≤ 15 | |
| x>0 et y>0 |
Premièrement on construit les deux droites
(D): 2x+y-5=0.
(D'): 3x+4y-15=0.
On résout le système suivant pour connaitre le point d'intersection des droites.
| { | 2x+y-5=0 |
| 3x+4y-15=0 |
On peut utiliser la méthode de substitution.
| { | y = -2x + 5 |
| 3x + 4(-2x + 5) - 15 = 0 |
signifie
| { | y = -2x + 5 |
| -5x + 5 = 0 |
signifie
| { | y = -2.1 + 5 = 3 |
| x = 1 |
ainsi (D)∩(D')={A(1 ; 3)}.
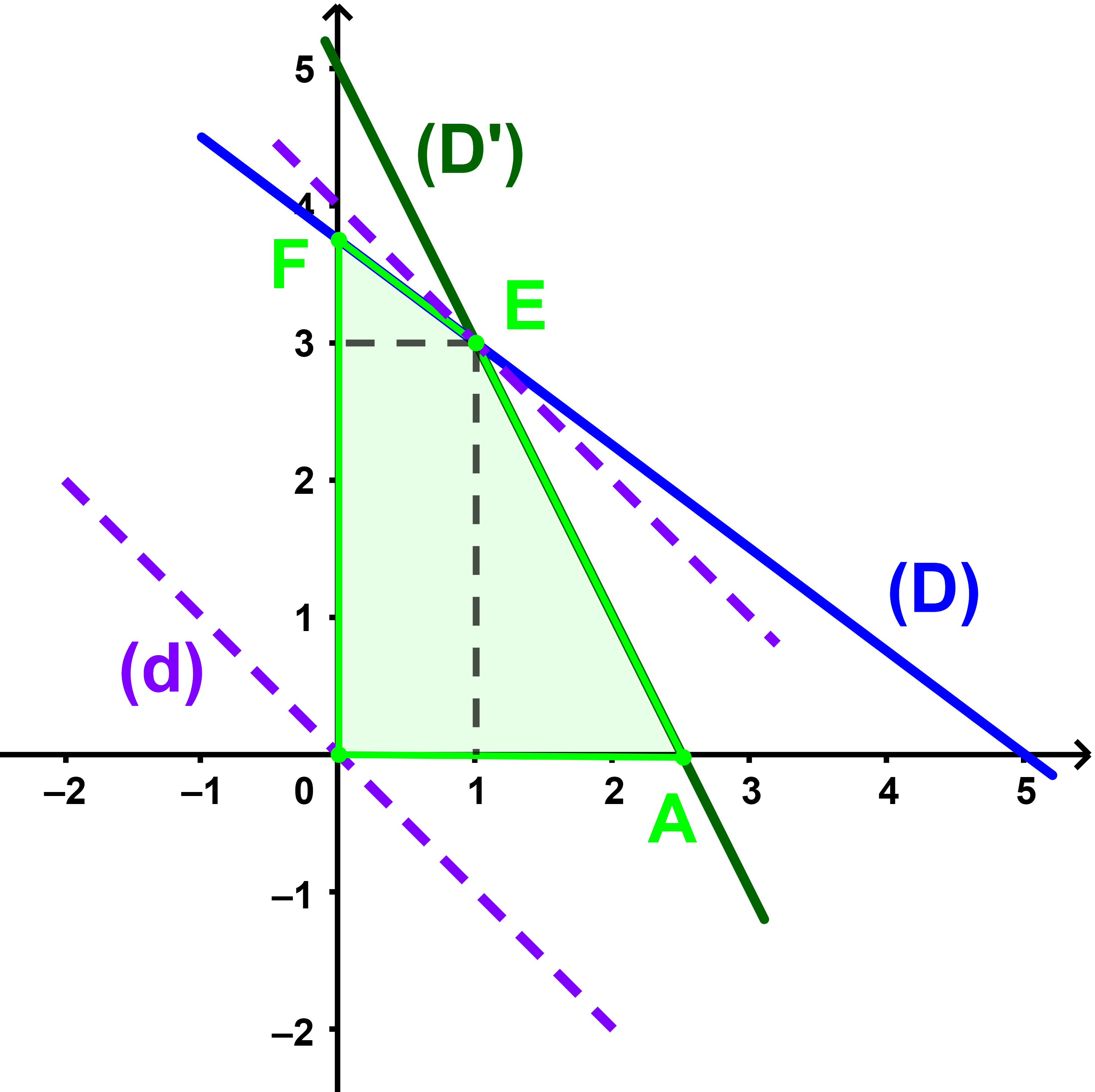
L'ensemble des solutions du système (S) est l'ensemble des points de la zone déterminée par le quadrilatère OAEF.
Et chaque point M(x;y) représente un profit possible b.
On a
750x+750y=b cette expression et selon les valeurs de b représente une équation des droites (d) parallèles et coupent le quadrilatère OAEF.
Le profit b sera maximum au point d'intersection le plus élevé de l'une de ces droite et du quadrilatère
à condition que ses coordonnées soient des entiers naturels. Cette intersection est le point E(1;3).
Un tapis de type T1 doit être fabriqué et trois tapis de type T2.
Le profit maximum possible est donc
b=750×1+750×3
ainsi b=3000 Dh.