Fonctions numériques (1)
1- Représentation graphique d'une fonction
1.1 Rappel
1.1.1 Définition
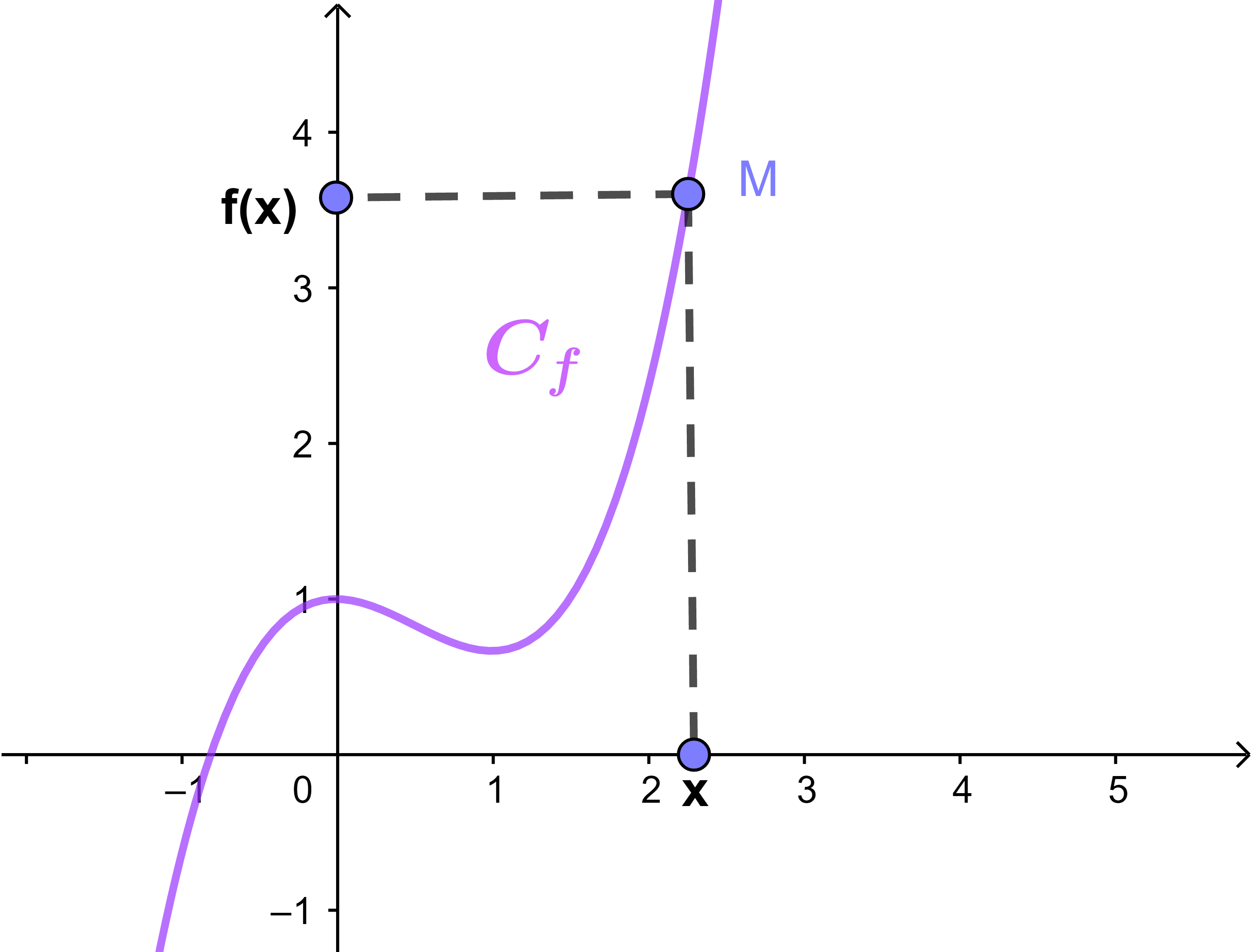
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). Soit f une fonction numérique de domaine de définition Df et (Cf) ou (C) sa courbe représentative.
M(x;y)∈(C) signifie x∈Df et y=f(x).
1.1.2 Tnterprétation graphique
2- fonction affine
2.1 Fonction linéaire
2.1.1 Rappel
La fonction numérique définie sur IR par
f(x)=ax tel que a∈IR* est appelée fonction linéaire.
2.1.2 Exemple 1
Soit f une fonction définie par f(x)=2x. Construisons (C) la courbe de f dans un repère orthonormé (O;i→;j→).
On détérmine quelques images convenables.
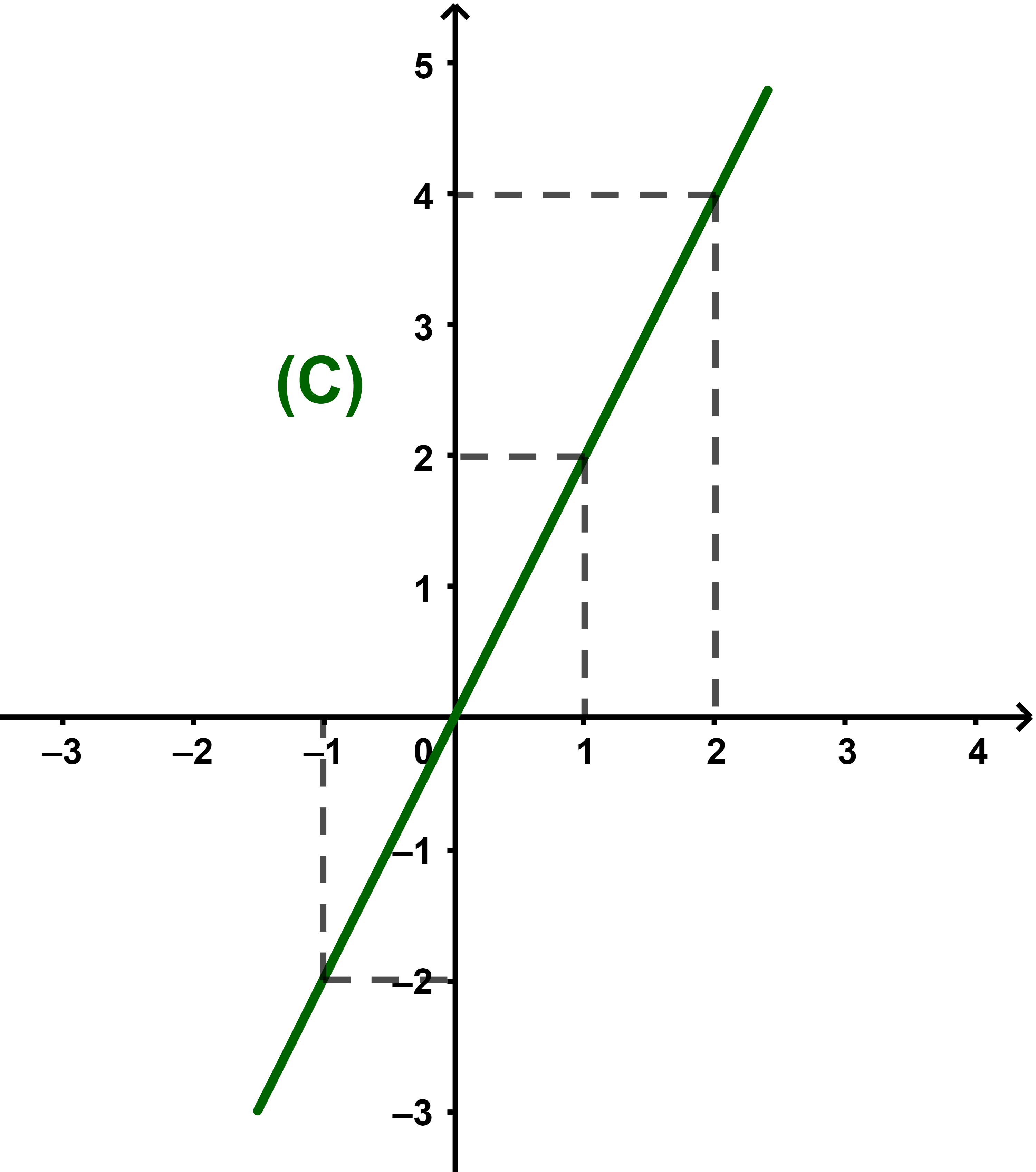
La courbe (C) est une droite et graphiquement f est strictement croissante sur IR.
| x | -∞ | +∞ | |
| f | ↗ |
Exemple 2
Soit g une fonction numérique définie par
| g(x) = | - 1 | x |
| 2 |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
Construisons (C) en déterminant quelques images par g.
| x | - 2 | 0 | 2 |
| g(x ) | 1 | 0 | -1 |
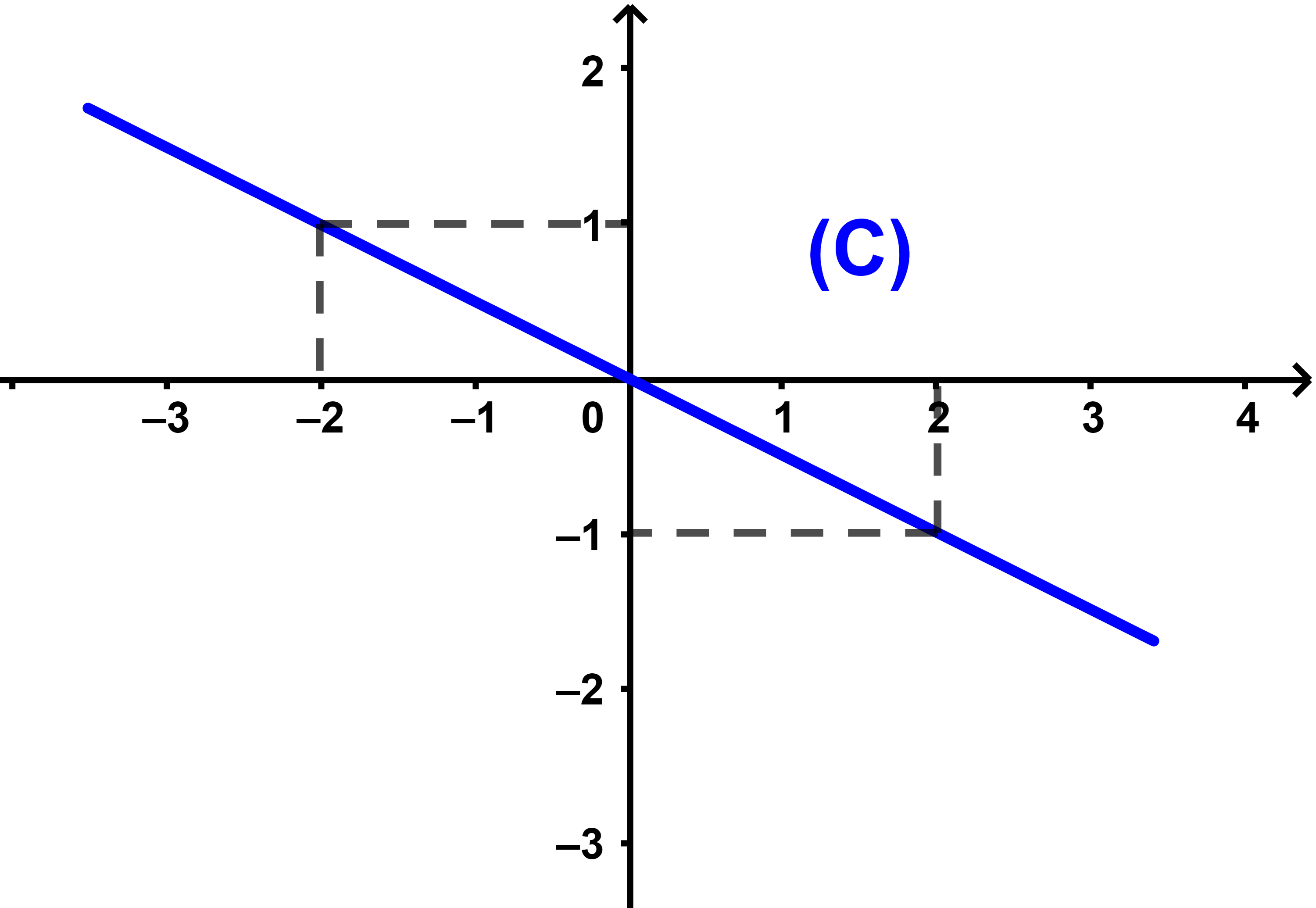
Remarque Les points de la courbe (C) sont alignés car l'équation de (C)
| y = | - 1 | x |
| 2 |
est une équation d'une droite passant par l'origine.
Graphiquement g est strictement décroissante sur IR.
| x | -∞ | +∞ | |
| g | ↘ |
2.1.3 Propriétés
Soit a un nombre réel non nul
et f la fonction linéaire de la variable réel x définie par
f(x)=ax.
1) La courbe de la fonction f est une droite d'équation y=ax.
2) Si a>0 alors f est strictement croissante sur IR.
3) Si a<0 alors f est strictement décroissante sur IR.