الدوال العددية (3)
1.3 التمثيل المبياني لدالة تآلفية معرفة على مجالات
1.3.1 مثال 1
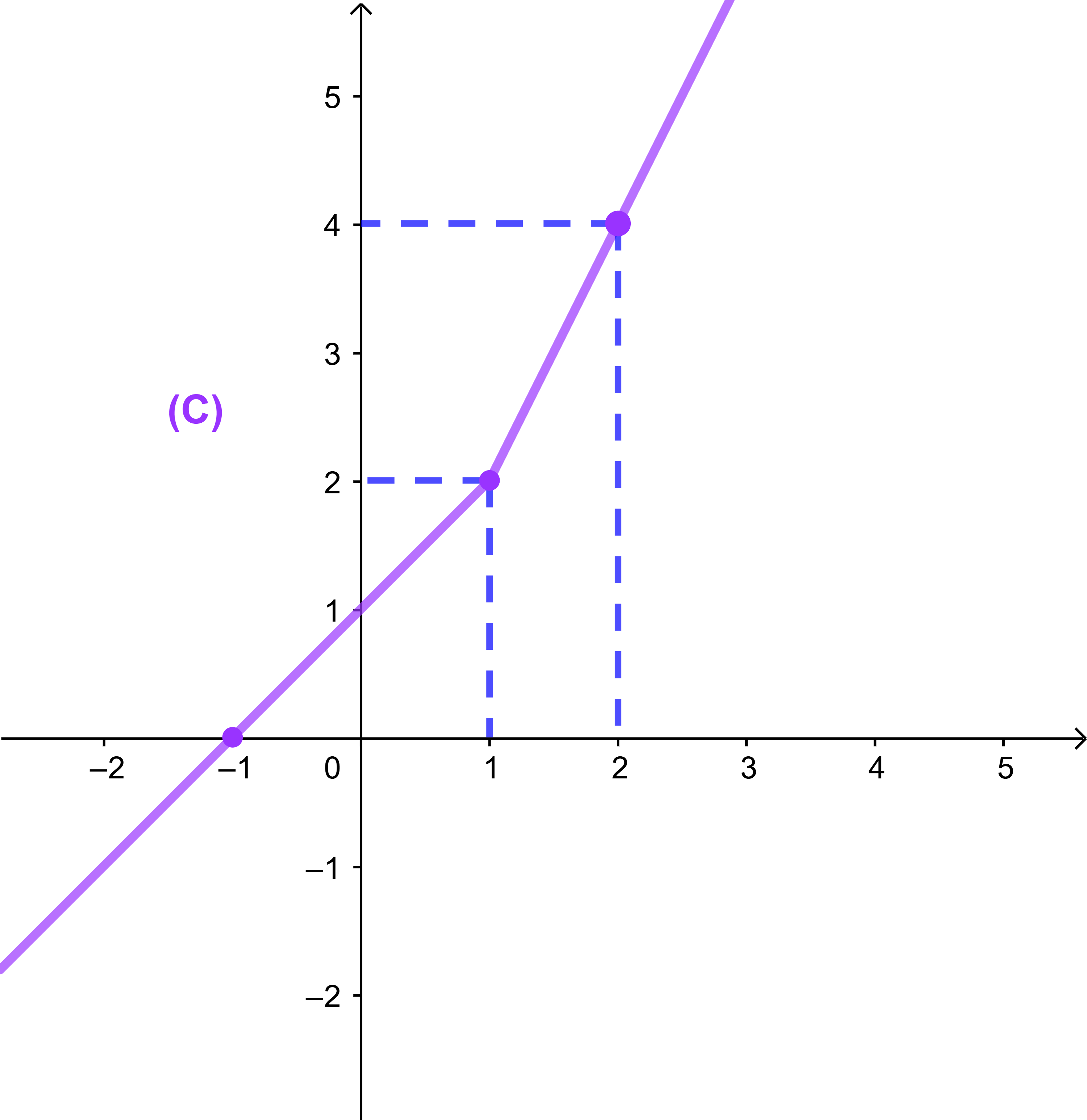
لتكن f دالة عددية معرفة على IR بما يلي
| { | f(x) = 2x | x ≥ 1 |
| f(x) = x+1 | x < 1 |
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i→;j→).
انشئ المنحنى (C).
تصحيح
f دالة عددية معرفة بالاجزاء
اذا كان x∈ ]-∞;1[ فان
f(x)=x+1.
اذا كان x∈ [1;+∞[ فان f(x)=2x.
منحنى الدالة f هو اذن اتحاد نصفي مستقيم
(D): y=x+1 حيث x<1
(D'): y=2x حيث x≥1.
مثال 2
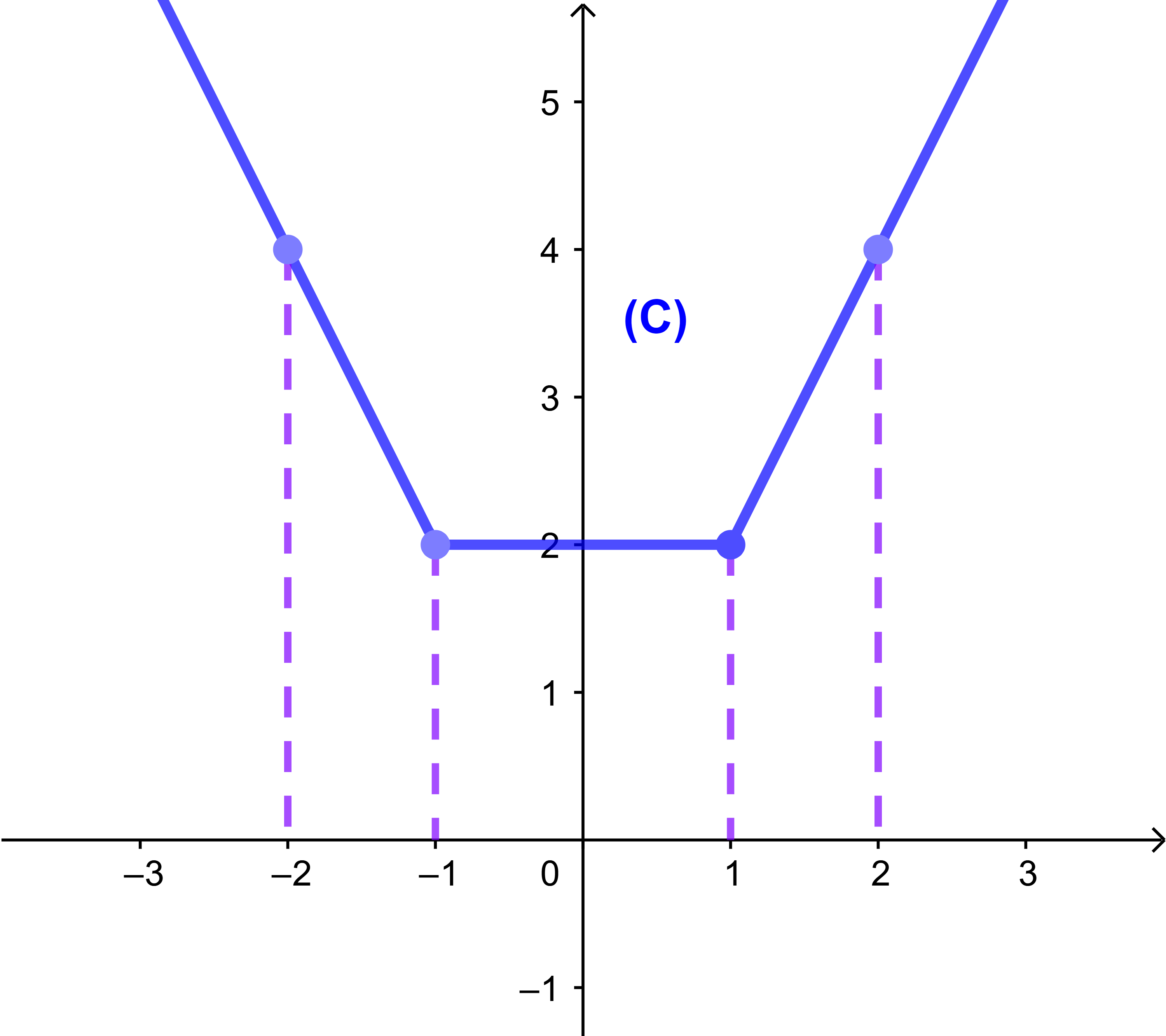
لتكن f دالة عددية معرفة على IR بما يلي
| { | f(x) = -2x | x < -1 |
| f(x) = 2 | -1≤x≤1 | |
| f(x) = 2x | (x≥1) |
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i→;j→).
انشئ النحنى (C).
تصحيح
f دالة عددية معرفة بالاجزاء
اذا كان x∈]-∞;-1[
فان f(x)=-2x
اذا كان x∈[-1;1]
فان f(x)=2
اذا كان
x∈[1;+∞[
فان f(x)=2x
وبالتالي منحنى الدالة f اذن هو اتحاد نصفي مستقيم وقطعة.
ملاحظة
مبيانيا الدالة f
تناقصية قطعا على المجال ]-∞;-1[
وثابتة على المجال [-1;1]
وتزايدية قطعا على المجال [1;+∞[.