Fonctions numériques (3)
2.2.3 Représentation graphique d'une fonction affine définie sur des intervalles
2.2.1 Exemple
Soit f une fonction numérique définie par
| { | f(x) = 2x | si x≥1 |
| f(x) = x+1 | si x < 1 |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
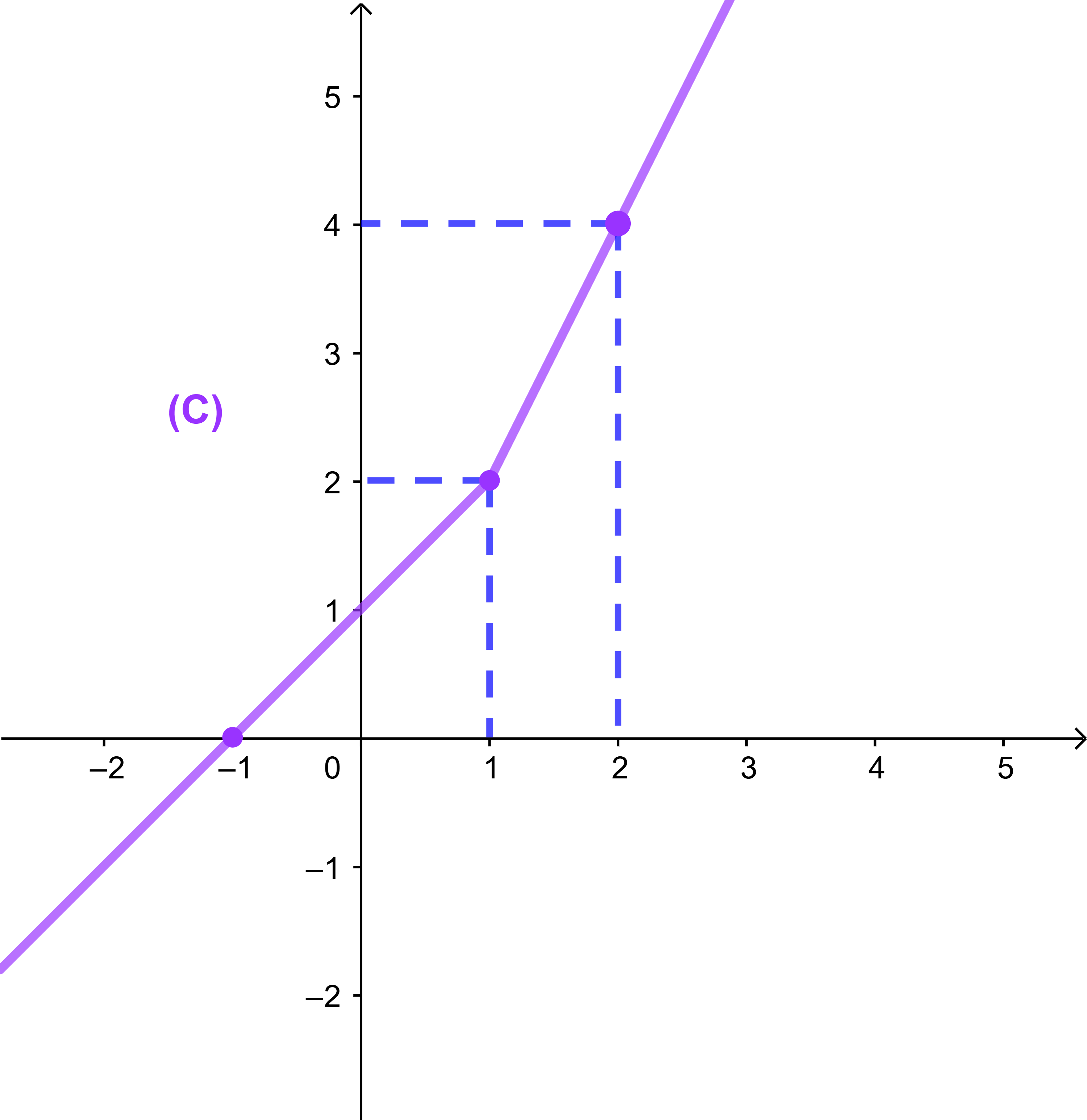
Tracer la courbe (C).
Correction
f est une fonction définie par des parties.
1) Si x∈]-∞;1[ alors f(x)=x+1.
2) Si x∈[1;+∞[ alors f(x)= 2x.
La courbe (C) est donc l'union de deux demi droites.
(D1): y=x+1 tel que x<1.
(D2): y=2x tel que x≥1.
Exercice 1 tp
Soit f une fonction numérique définie par
| { | f(x) = 2x | si x > 1 |
| f(x) = 2 | si -1 ≤ x ≤ 1 | |
| f(x) = -2x | si x < -1 |
et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
Construire la courbe (C).
Correction
f est une fonction définie par des parties.
Si x∈]-∞;-1[ alors f(x)=-2x.
Si x∈[-1;1] alors f(x)=2.
Si x∈[1;+∞[ alors f(x)=2x.
Ainsi la courbe (C) est l'union de deux demi-droites et un segment.
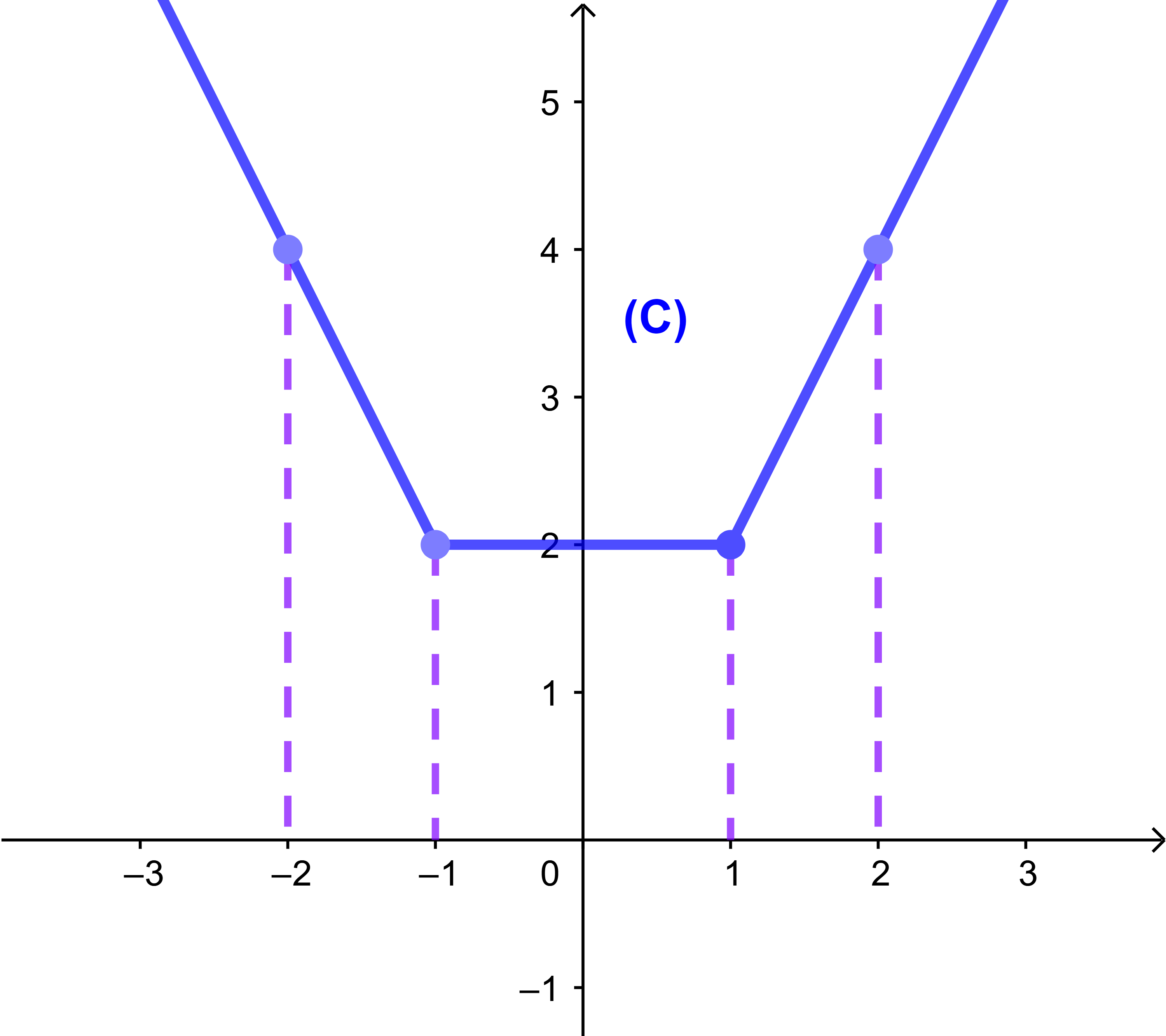
Graphiquement
f est strictement décroissante sur ]-∞;-1[.
f est constante sur [-1;1].
f est strictement croissante sur [-1;+∞[.