Equations Inéquations et Systèmes (1)
1- Equations et inéquations du premier degré à une inconnue
Lorsque votre téléphone sonne avant que vous ne le regardiez pas, vous ne savez pas qui appelle.
Vous avez donc une équation à une inconnue et vous souhaitez la résoudre :)
1.1 Equations du premier degré à une inconnue
1.1.1 Activité et rappel
Amine a 100DH, il a acheté deux billets pour assister à un match
de football et il le reste 30DH.
Combien le prix d'un billet ?
Correction
On désigne par x le prix d'un billet
2x+30=100 signifie 2x+30+(-30)=100+(-30)
signifie 2x=70 signifie x=35
ainsi l'ensemble de solutions de l'équation
S={35} et le prix d'un billet est donc 35DH.
1.1.2 Définition
L'équation du premier degré à une inconnue s'écrit sous la forme ax+b=0 tels que x est l'inconnue et (a et b sont des constantes).
1.1.3 Résolutions de l'équation ax+b=0
1) Soit S l'ensemble des solutions de l'équation ax+b=0.
| Si a≠0 alors x = | -b |
| a |
| donc S = { | -b | } |
| a |
2) Si a=0 alors ax+b = 0 équivaut à 0x+b=0.
(a) Si b=0 alors 0x=0 est vraie pour tout réel x
et donc S=IR.
(b) Si b≠0 alors 0=b≠0
et ce n'est pas possible donc S=∅.
Exercice 1 tp
Résoudre dans IR l'équation 4x+5=0.
Correction
Soit x∈IR.
4x+5=0 signifie
4x=-5
signifie
| x = | -5 |
| 4 |
| ainsi S = { | -5 | } |
| 4 |
Exercice 2 tp
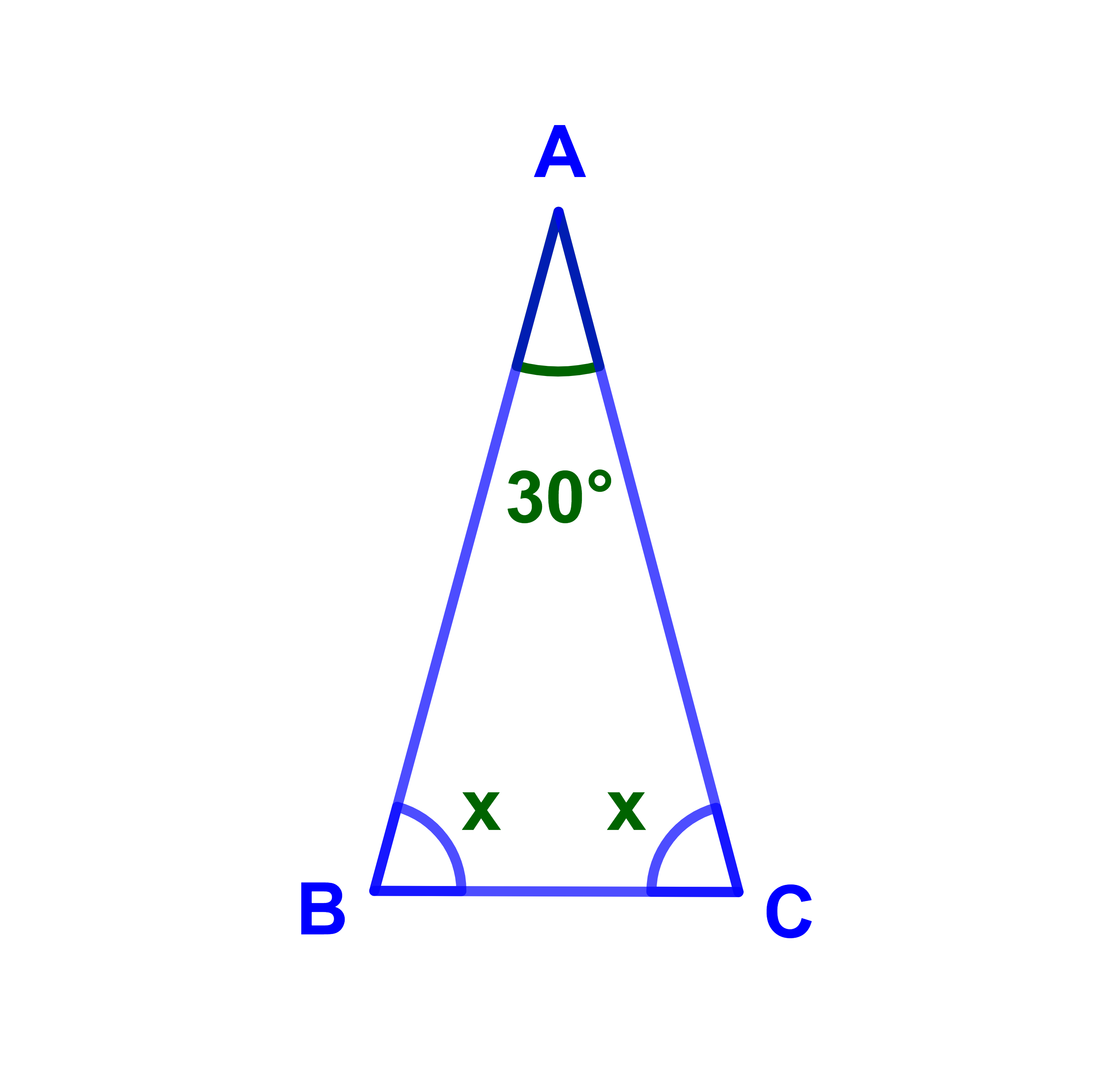
Soit ABC un triangle isocèle. Calculer x.
Exercice 3 tp
Résoudre dans IR l'équation
3x-9=0.
Correction
Soit x∈IR.
3x- 9=0 signifie
3x=+9
signifie
| x = | 9 | = 3 ∈IR |
| 3 |
ainsi l'ensemble de solutions de l'équation
S = { 3 }.
Exercice 4 tp
Résoudre dans IR l'équation
3(x+5)-5(x+3)=0.
Correction
Soit x∈IR.
3(x+5)-5(x+3) = 0
signifie
3x+15-5x-15=0
signifie
3x-5x+15-15=0
signifie
(-2x) 0
(-2≠0) donc x=0∈IR
ainsi S={ 0 }.