(21) المعادلات والمتراجحات والنظمات
3.3.3 البرمجة الخطية
مسألة
جمعية نسوية تصنع نوعين من الزرابي T1 و T2 خلال النهار تستعمل الآلة وخلال الليل تستعمل اليد وخصصت لذلك ميزانية تقدر ب 5000 درهم للمواد الاولية 15000 درهم لليد العاملة وكل زربية تحقق مكاسب قدرها 750 درهم
علما ان كل زربية من نوع
T1 تتطلب 2000 درهم للمواد الاولية و 3000 درهم لليد العاملة وكل زربية من النوع
T2
تتطلب 1000 درهم للمواد الاولية و 4000 درهم لليد العاملة
كم زربية من كل نوع يمكن صناعتها لتحقيق اقصى ربح ممكن ؟
تصحيح
نعين ب x و y لعدد الزرابي على التوالي من نوع T1 و T2.
| النوع | T1 | T2 | المجموع |
| المواد الاولية | 2000/1 | 1000/1 | 5000 |
| اليد العاملة | 3000/1 | 4000/1 | 15000 |
المواد الاولية ممثلة بالمتراجحة
2000x + 1000y ≤ 5000
واليد العاملة ممثلة بالمتراجحة
3000x+4000y ≤ 15000
ولدينا بالطبع
x>0 و y>0 اعداد طبيعية
الزوج (x ; y) يحقق النظمة التالية
| { | 2000x + 1000y ≤ 5000 |
| 3000x + 4000y ≤ 15000 | |
| x>0 ; y>0 |
التي تكافئ
| (S) : { | 2x + y ≤ 5 |
| 3x + 4y ≤ 15 | |
| x>0 ; y>0 |
أولا ننشئ المستقيمين
(D): 2x + y - 5 = 0
(D'): 3x + 4y - 15 = 0
نحل النظمة التالية لمعرفة نقطة تقاطع المستقيميين
| { | 2x + y - 5 = 0 |
| 3x + 4y - 15 = 0 |
نستعمل طريقة التعويض اذن
| { | y = -2x + 5 |
| 3x + 4(-2x + 5) - 15 = 0 |
يعني
| { | y = -2x + 5 |
| -5x + 5 = 0 |
يعني
| { | y = -2.1 + 5 = 3 |
| x = 1 |
ومنه فان (D) ∩ (D') = {A(1 ; 3)
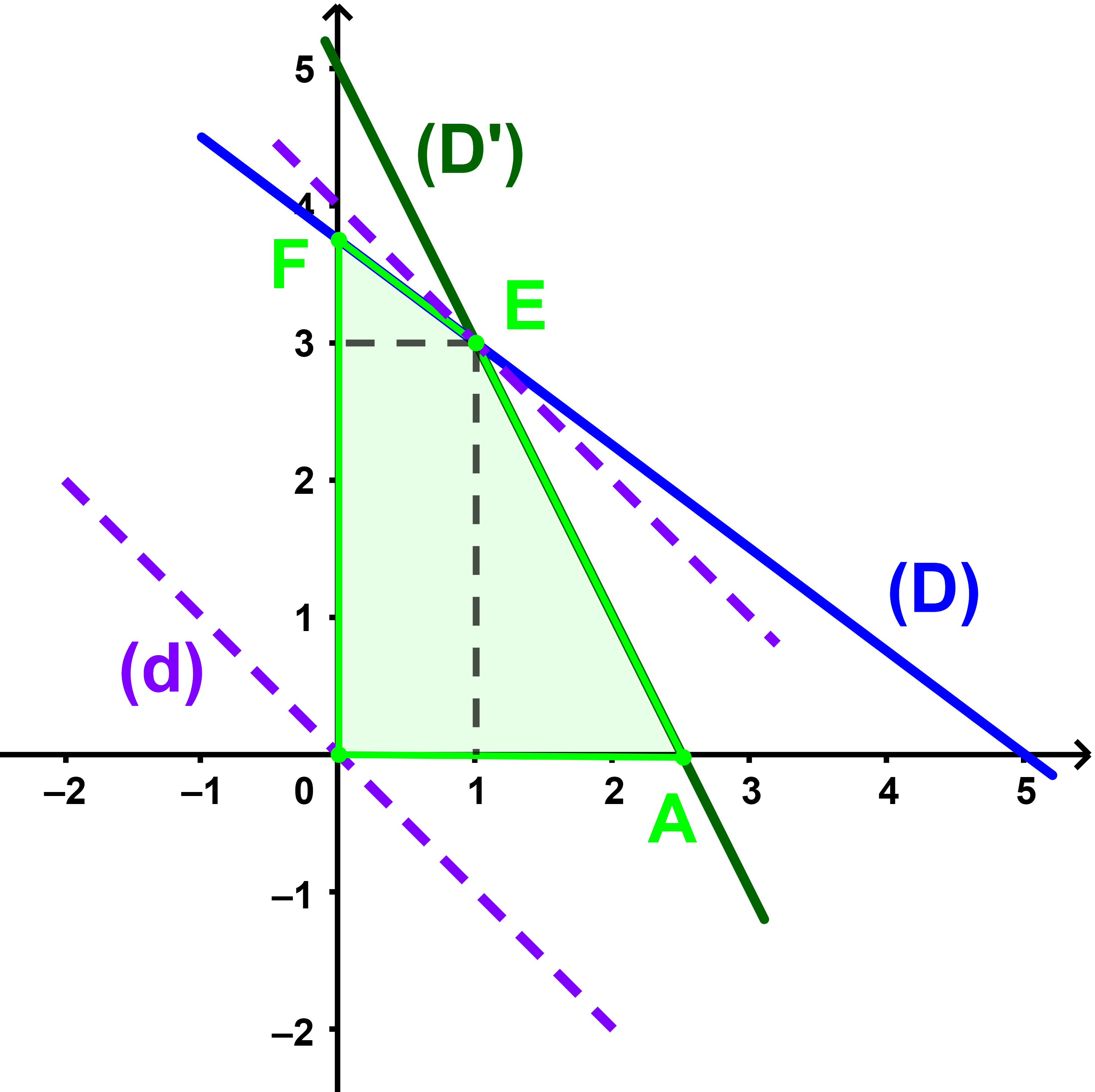
حلول النظمة (S)
هي مجموعة ازواج احداثيات نقط الجزء المحدد بالرباعي
OَAEF
وكل نقطة M(x;y) تمثل ربح ممكن نرمز له ب b
لدينا
750x+750y =b هذا التعبير وحسب قيم b يمثل معادلة
لمستقيمات (d) متوازية وتخترق الرباعي OAEF
والربح يكون أقصوى ما يمكن في اعلى نقطة تقاطع احدى هذه المستقيمات والرباعي مع شرط ان تكون احداتياتها مكونة من اعداد طبيعية وفي هذه المسألة هذه النقطة هي E(1;3).
ينبغي اذن صناعة زربية واحدة من النوع T1
و 3 من النوع T2
اذن اقضى ربح ممكن هو
b=750×1+750×3
وبالتالي b=3000 درهم.