La géométrie dans lspace (2)
Exercice 1 tp
Soit TBCD un tétraèdre tel que le triangle
BCD soit équilatéral
les triangles TDB et TCD soient rectangles en T.
On considère les points I et J respectivement les milieux des segments [BD] et [DC].
1) Déterminer la position relative des plans (TBC) et (TIJ).
2) Montrer que (TD)⊥(BC).
3) Montrer que (BC)⊥(TDC).
Exercice 2 tp
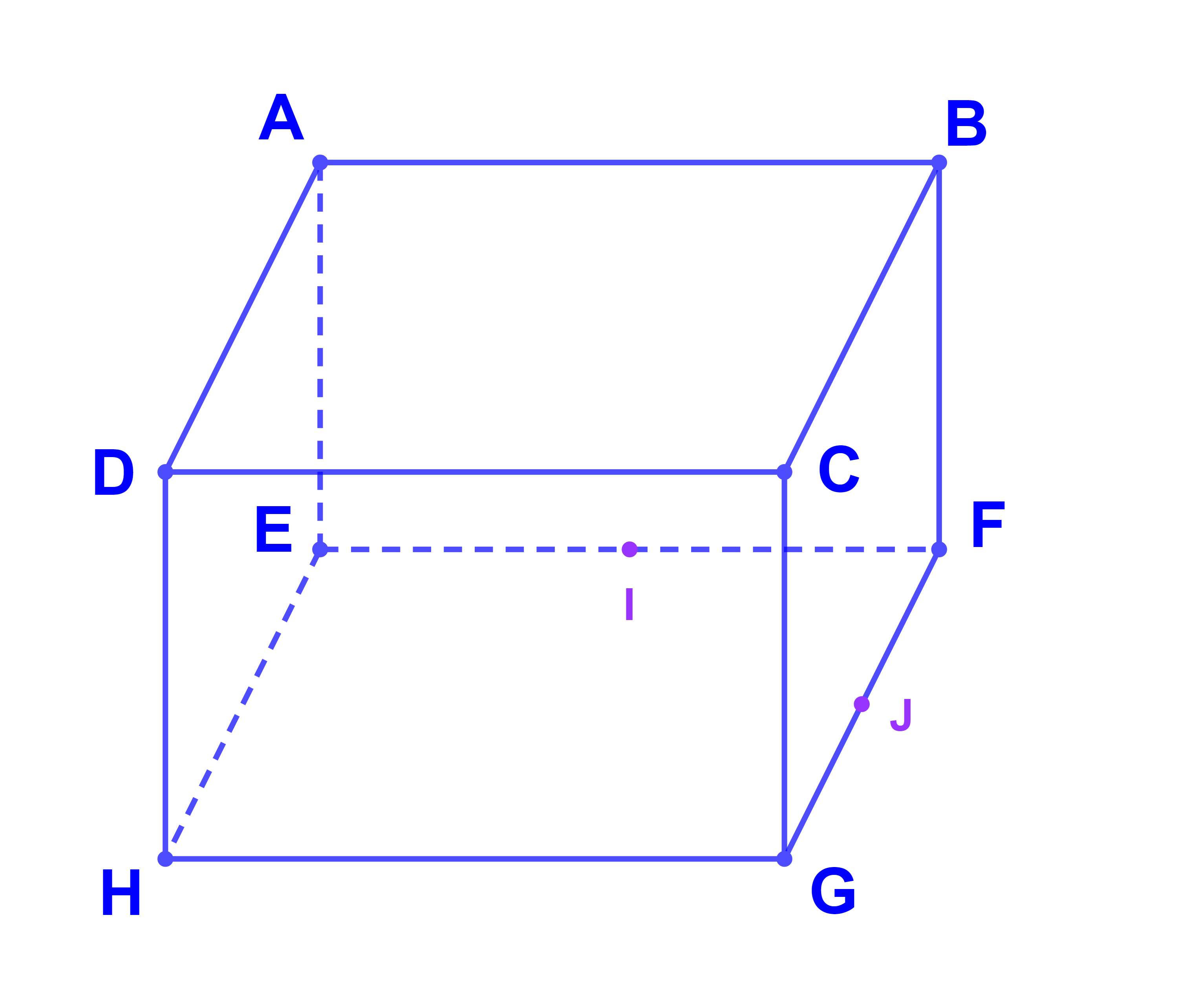
Soient ABCDEFGH un parallélépipède rectangle
I et J les milieux respectifs de [EF] et [FG].
1) Justifier que (BI) et (AE) se coupent en un point noté K.
et (BJ) et (GC) se coupent en un point noté L
2) Montrer que (KL)||(ABCD).
Exercice 3 tp
Soit TBCD un tétraèdre dont les faces sont des triangles équilatéraux.
Démontrer que
1) (TB)⊥(DC).
2) (BC)⊥(TD).
3) (BD)⊥(TC).
Exercice 4 tp
TBCD est un tétraèdre; I ; J et K sont des points respectifs des aretes [BC] ; [TC] et [TD]
tels que (IJ)||(TB) et (JK)||(CD).
1) Soit (Δ) une droite parallèle notée à la droite (CD) passant par I.
Montrer que (Δ)⊂(IJK).
2) On considère que la droite (Δ) coupe (BD) en L.
Montrer que (KL)||(TB).