Exercice 1 tp

Soit f une fonction numérique définie par
f(x)= 4x-x².
1) Etudier la monotonie de f sur ]-∞;2] et sur [2;+∞[.
2) Tracer le tableau de variations de f.
3) Déduire un extremum de f.
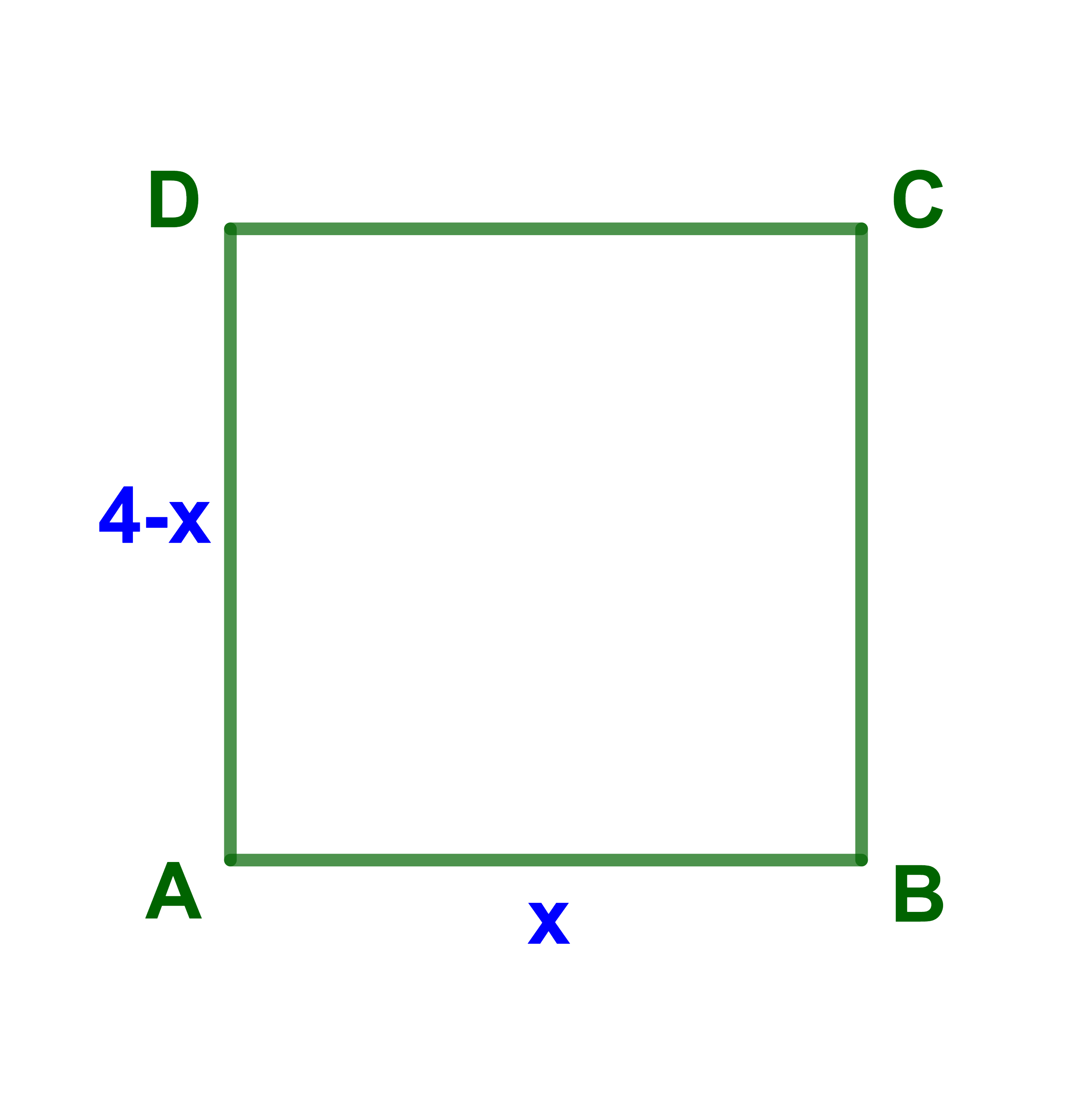
4) Soit ABCD un rectangle tels que
AB=x et AD=4-x.
Déterminer x de sort que la surface du rectangle soit maximale.

Correction

1) f est un polynôme donc D=IR.
Soient x; y ∈IR tels que x≠y
f(x)-f(y)=4x-x²-(4y-y²)
=-x²+y²+4x-4y
=-(x²-y²)+4(x-y)
=-(x-y)(x+y)+4(x-y)
=(x-y)(-x-y + 4).

Donc f(x)-f(y)=(x-y)[-(x+y)+4]
ainsi le taux d'accroissement T(x;y) de f entre x et y

T(x;y) =	f(x) - f(y)
	x-y

ou encore T(x;y)=-(x+y)+4.
1) Monotonie de f sur I=]-∞;2]
x; y ∈I signifie x≤2 et y≤2
donc x+y<4 (l'inégalité est stricte car x et y sont différents donc ne peuvent pas prendre la même valeur 2 en même temps).

Signifie -(x+y)>-4
signifie -(x+y)+4>0
donc T(x;y)>0 et cela signifie que f est strictement croissante sur I=]-∞;2].
2) Monotonie de f sur J=[2;+∞[
x; y ∈I signifie x≥2 et y≥2
donc x+y>4 (l'inégalité est stricte car x et y sont différents donc ne peuvent pas prendre la même valeur 2 en même temps)
signifie -(x+y)<-4.

Signifie -(x+y)+4<0
donc T(x;y)<0 et cela signifie que f est strictement décroissante sur J=[2;+∞[.
2) Tableau de variations: on a f(2)=4.

x		-∞		2		+∞
f			↗	4	↘

3) f est strictement croissante sur ]-∞;2] et strictement décroissante sur [2;+∞[ donc f admet une valeur maximale 4 au point 2 ainsi 4=f(2) est un extremum de la fonction f.

4) ABCD est un rectangle.
La surface du rectangle S(x)=x(4-x)
ou encore S(x)=4x-x².

On considère donc la fonction f
S est maximale au point a tel que f(a) est une valeur maximale.
D'après la question précédente 4 est une valeur maximale de f au point a=2
et donc S est maximale si x=2
de plus AB=2 et AD=4-2=2 alors ABCD est un carré de coté 2.