Exercice 1 tp

Soit x∈IR. A quel intervalle appartient x
tel que 2x+3≤7 ?

Correction

2x+3≤7 signifie que 2x≤7-3
ou encore 2x≤4 ou encore x≤2
donc x∈]-∞;2].
-∞ --- 2 --- → +∞

Exercice 2 tp

Soit x∈IR. A quel intervalle appartient x
tel que -3x+4≥13 ?

Correction

-3x+4≥12 signifie que -3x≥13-4
ou encore -3x≥9 ou encore 3x≤-9
donc x≤-3 ainsi x∈]-∞;-3].
-∞ --- -3 --- → +∞

Exercice 3 tp

Soient x∈IR\{-2} et A un nombre réel défini par

A =	1
	x+2

si 2<A<4
à quel intervalle appartient x ?

Correction

Puisque A est compris entre deux nombres strictement positifs alors il est strictement positif donc x+2 est strictement positif.

2 <	1	< 4
	x+2
1	< x+2 <	1
4		2
1	- 2 < x < -2 +	1
4		2
- 7	< x <	- 3
4		2

donc x ∈ ]	- 7	;	- 3	[
	4		2

Exercice 4 tp

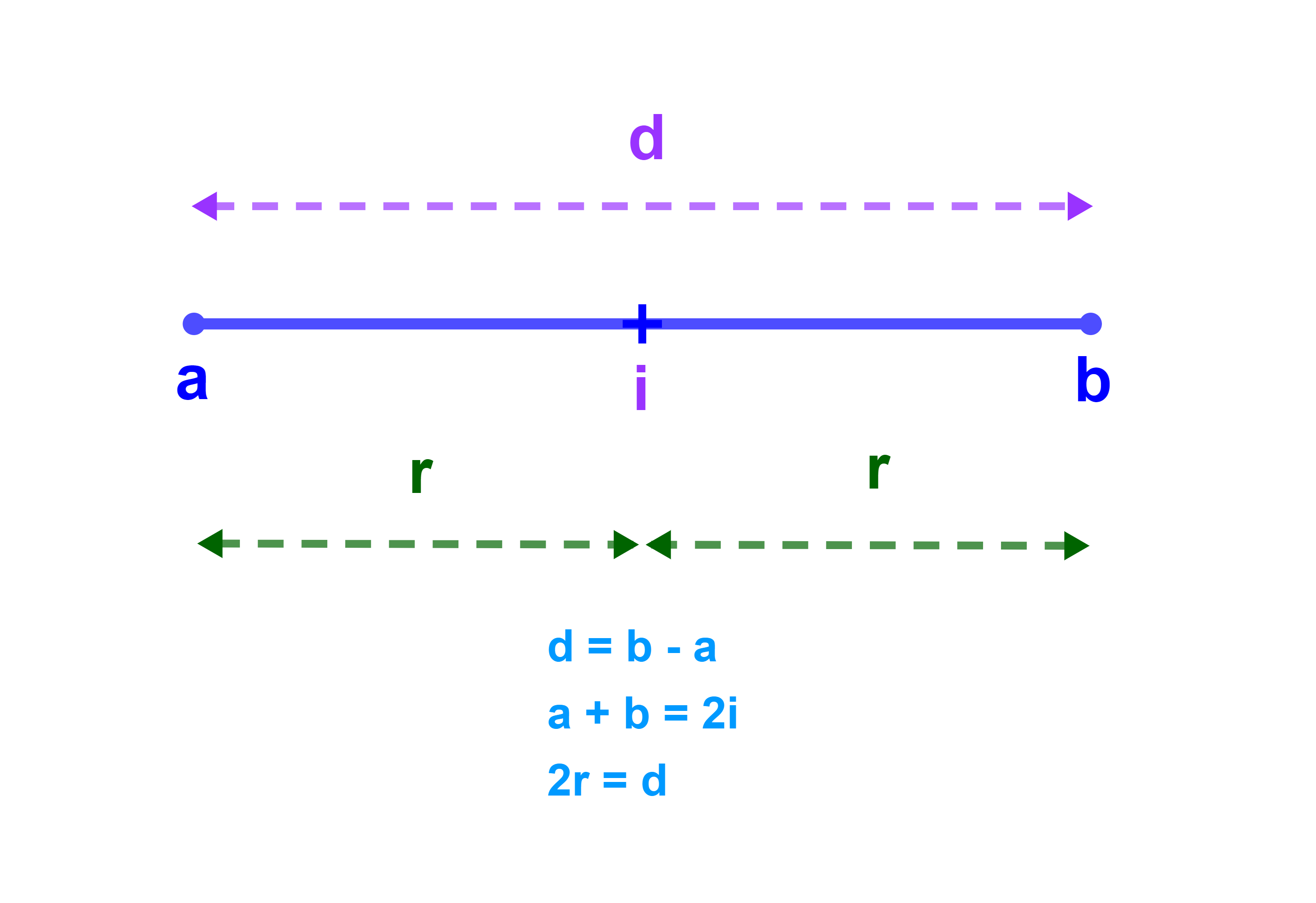
Soit I=[2;12] un intervalle.
Déterminer le centre et le rayon de I.

Correction

On désigne par i au centre et par r au rayon

{	i =	2+12	= 7
		2
	r =	12-2	= 5
		2

donc 7 est le centre de I et 5 son rayon.

Exercice 5 tp

1) Soit I un intervalle de centre 10 et de rayon 12. Déterminer I.
2) Soit J=]5;b[ de rayon 7. Déterminer b et le centre i.

Correction

1) méthode 1
On sait que b-a=d=2×12=24
et a+b=2i=2×10=20.
On résout le système suivant

{	-a + b = 24
	a + b = 20

en additionnant membre à membre les deux membres des équations on obtient
2b=24+20=44 donc b=22.

Puis on remplace la valeur de b dans l'une des deux équations
a+22=20 donc a=-2 ainsi I=[-2;22].
méthode 2
a=i-r=10-12=-2
et b=i+r=10+12=22.
2) On a J=]5;b[ et r=7
donc b-5=2r=14 ainsi b=19
et on a a+b=2i ou encore 5+19=2i
ou encore 2i=24 donc i=24÷2=12.