1- المتجهات

1.1 مفهوم متجهة

1.1.1 تقديم

➀ ما معنى مستوى ?

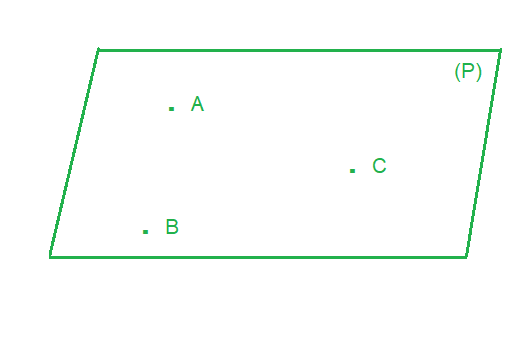
المستوى هو مجموعة غير منتهية من النقط بحيث اذا اعتبرنا اربع نقط مختلفة A و B و C و D منه فان المستقيمين (AB) و (CD) متوازيان أو متقاطعان.
➁ ما معنى متجهة ?
↗
(a) نقطتان مختلفتان A و B تحددان اتجاها للمستقيم (AB).
(b) توجيه القطعة [AB] يحدد منحى .
(c) طول القطعة [AB] يحدد المنظم.

1.1.2 تعريف

تعرف المتجهة ب
1) اتجاه.
2) منحى.
3) المنظم أو المسافة.

ترميز
1) تمثل المتجهة بحرف فوقه سهم u^→ أو حرفان AB^→ .
2) الكتابة ||u^→|| تمثل منظم المتجهة u^→.

3) لتكن A و B نقطتين من المستوى.
(a) اذا كان u^→=AB^→ فان منظم المتجهة u^→ هو مسافة A الى B
ونكتب ||u^→||=||AB^→||=AB.

(b) اذا كانت A=B فان المتجهة AA^→ تسمى المتجهة المنعدمة ونرمز لها ب O^→.
(c) ||u^→||=0 يعني u^→=O^→.

1.2 تساوي متجهتين

1.2.1 تعريف

لتكن u^→ و v^→ متجهتين.
u^→ و v^→ متساويتان ونكتب u^→=v^→ اذا كانت لهما
1) نفس الاتجاه.
2) نفس المنحى.
3) نفس المنظم.

بعبارة أخرى
u^→ و v^→ متساويتان اذا كانتا ممثلثين بقطعتين موجهتين ومتوازيتين ولهما نفس المسافة.

1.2.2 خاصية

لتكن A و B و C و D أربع نقط من المستوى.
AB^→=DC^→ يكافئ ABCD متساوي الأضلاع.

1.3 متجهات متقابلة

1.3.1 تعريف

نقول ان u^→ و v^→ متجهتان متقابلتان ونكتب u^→=-v^→ اذا كان لهما نفس الاتجاه ونفس المنظم ومنحيين متقابلين.

1.3.2 التمثيل