1- التماثل المركزي

1.1 تعريف وتمثيل هندسي

1.1.1 تعريف

لتكن O نقطة من المستوى.
التحويل الهندسي الذي يربط كل نقطة M من المستوى بنقطة M' بحيث O منتصف القطعة [MM'] يسمى التماثل المركزي مركزه O ونرمز له ب S_O.

بتعبير آخر S_O(M)=M' يعني O منتصف [MM'].

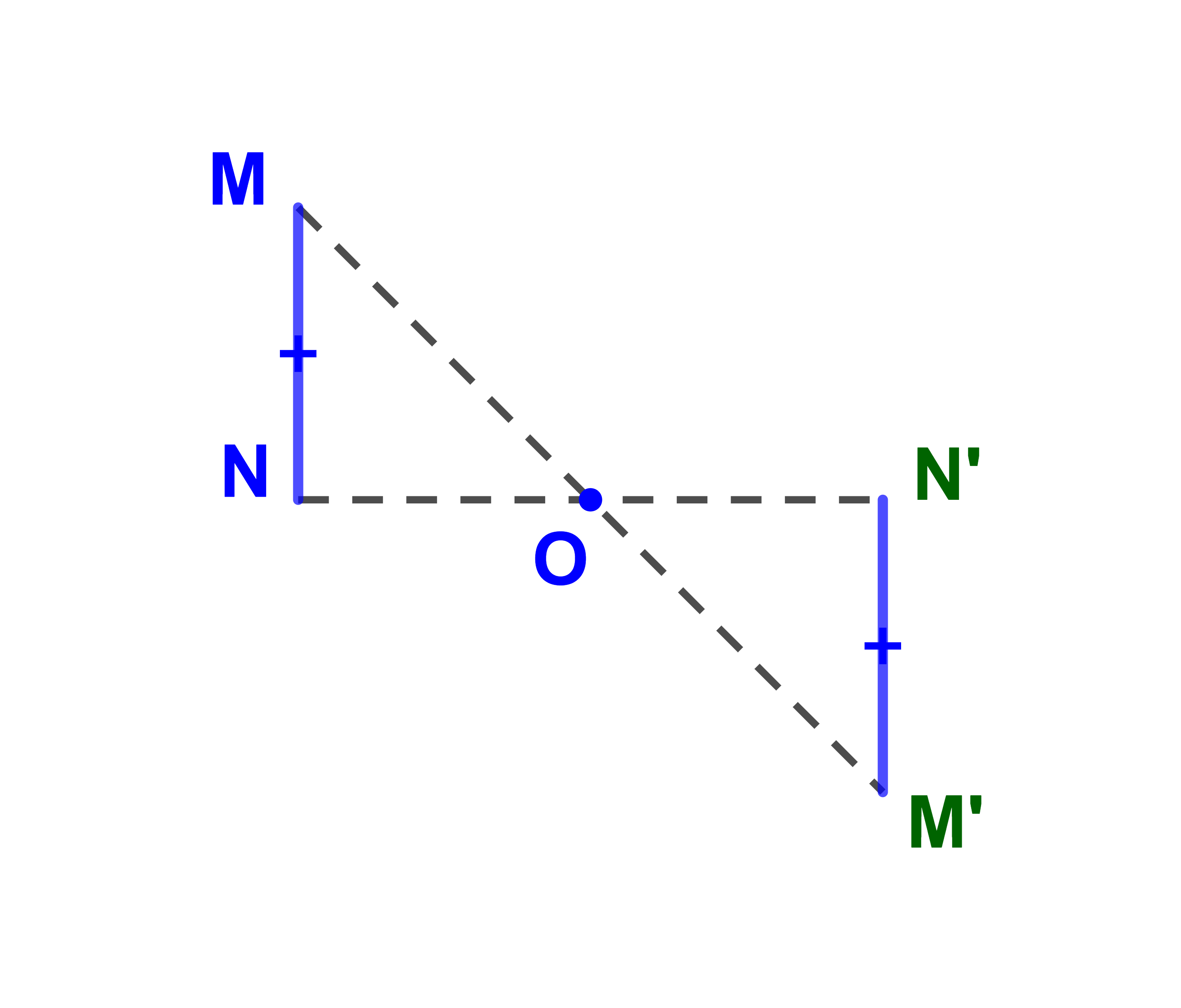
1.1.2 التمثيل المبياني

لتكن M نقطة و M' صورتها بتماثل مركزي S_O.

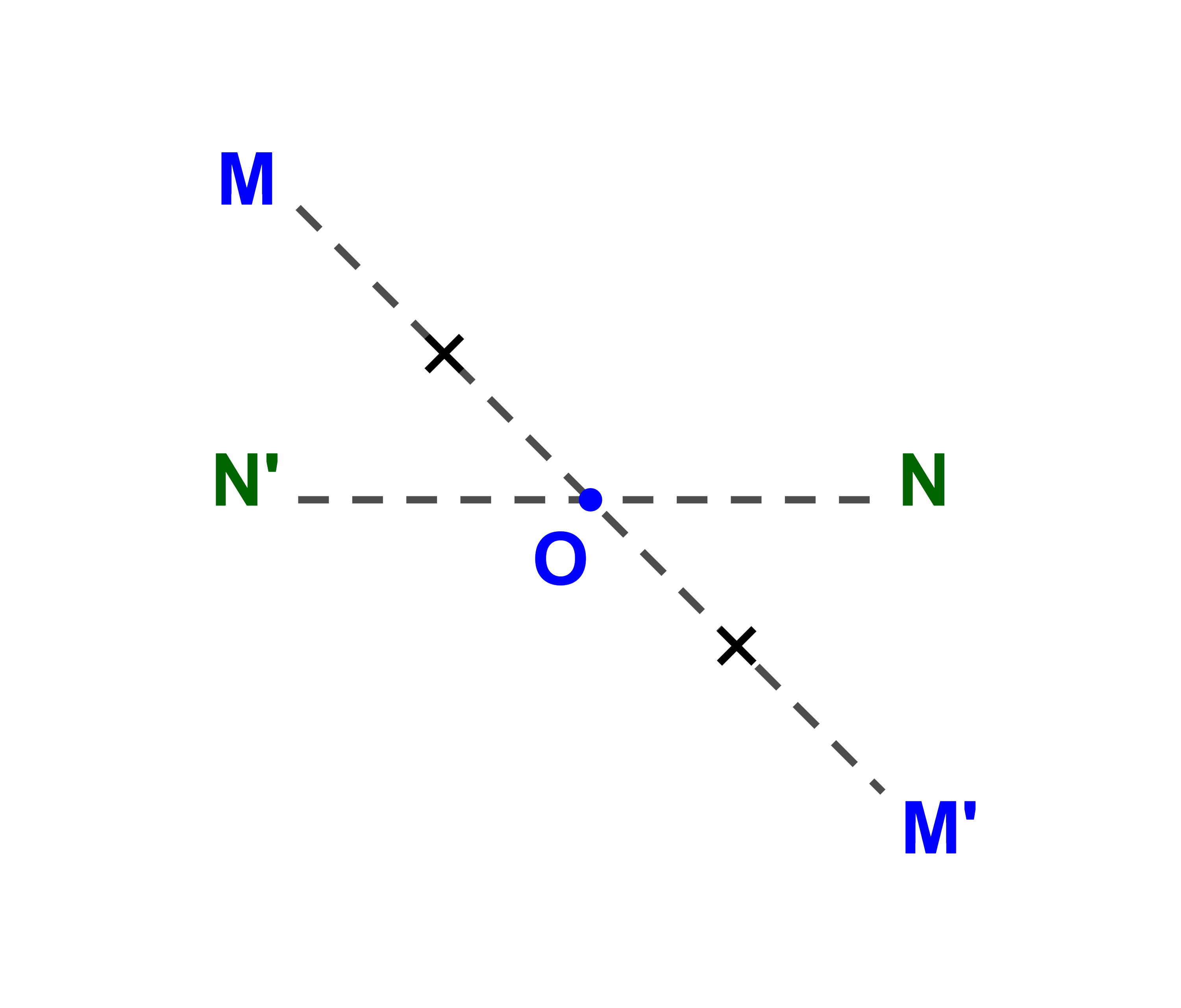
ملاحظة
التماثل المركزي يقبل نقطة صامدة واحدة وهي المركز O.

2) I نقطة صامدة بتحويل T يعني T(I)=I.

تمرين 1 tp

ليكن EFG مثلثا قائما في F.
انشئ المثلث E'F'G' صورة المثلث EFG بالتماثل المركزي الذي مركزه E وحدد طبيعته.

1.1.3 الخاصية المميزة لتماثل مركزي

يكون تحويل T تماثلا مركزيا اذا وفقط اذا كان
لكل نقطتين M و N لدينا M'N'^→=-MN^→
بحيث M'=T(M) و N'=T(N).

1.2 الحفاظ على معامل استقامية متجهتين

1.2.1 تقاطع

1) u^→ و v^→ متجهتان ستقيميتان يعني يوجد عدد حقيقي k بحيث v^→=ku^→.
2) توجد ثلاث نقط A و B و C بحيث
u^→=AB^→ و v^→=AC^→
اذن AC^→=kAB^→.

حسب الخاصية المميزة لتماثل مركزي فان
A'B'^→=-AB^→ و A'C'^→=-AC^→
اذن -A'C'^→=-kA'B'^→
ومنه فان A'C'^→=kA'B'^→
(المعامل k لا يتغير).

1.2.2 خاصية

التماثل المركزي يحافظ على معامل استقامية متجهتين.

1.2.3 نتائج

التماثل المركزي يحافظ على استقامية النقط وعلى منتصف قطعة

1.2.4 المسافة والتماثل المركزي

خاصية
ليكن S تماثلا مركزيا.
مسافة نقطتين هي نفس مسافة صورتاهما بالتماثل المركزي S.
بتعبير آخر اذا كان S(A)=A' و S(B)=B'
فان A'B'=AB.

نتيجة التماثل المركزي يحافظ على المسافة.