Exercice 1 tp

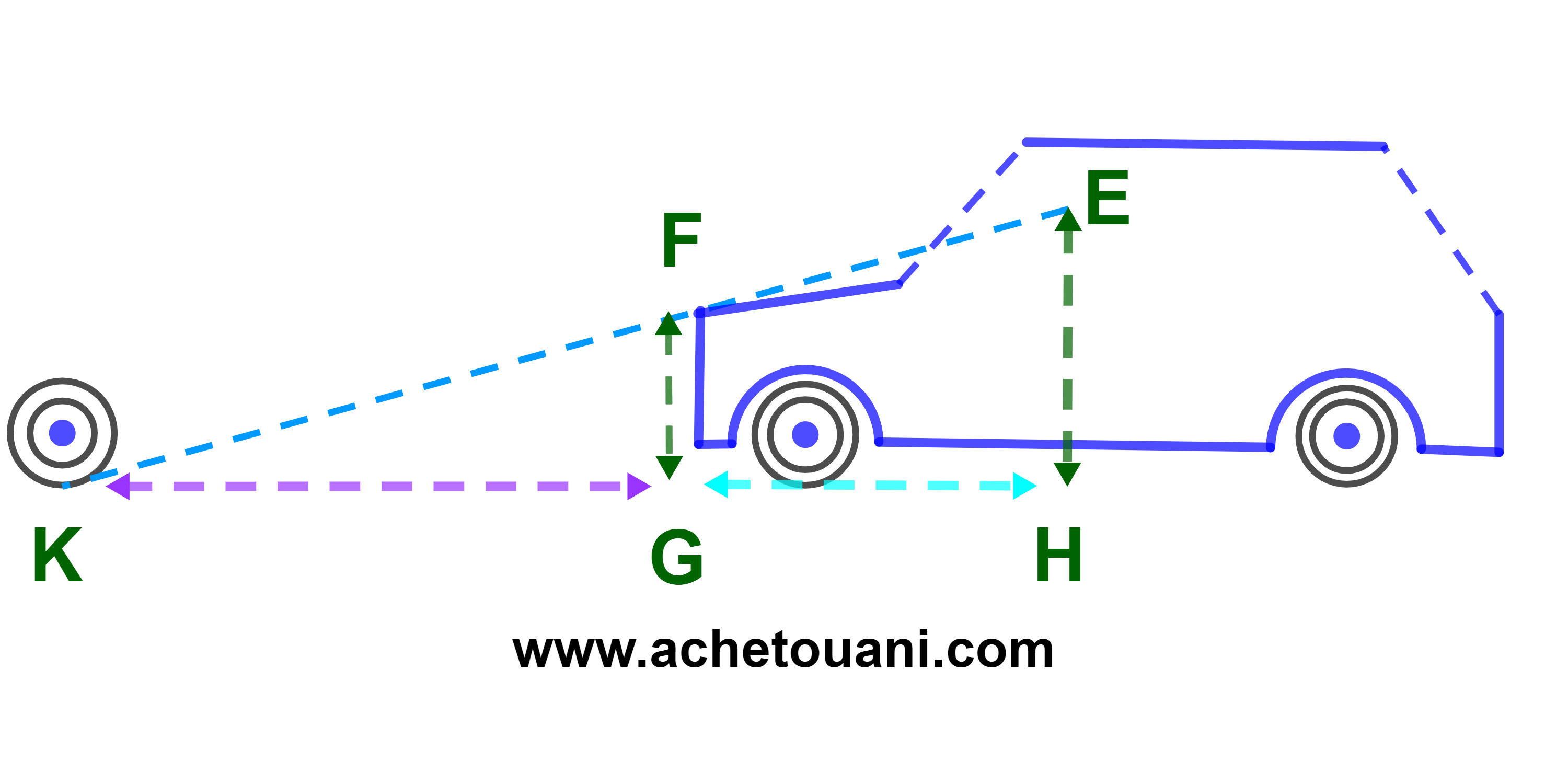
Un automobiliste veut se tenir derrière un véhicule garé au signal devant lui et regarder ses roues arrière.
Il s'arrete quand son regard est droit avec elles exactement avec l'avant de sa voiture.
On suppose que la distance séparant son regard et la surface de la terre est EH=135cm
la hauteur de l'avant de sa voiture est de FG=80cm.

La distance entre l'avant de sa voiture et la projection de vue sur la terre est GH=220cm.
1) Calculer KG la distance entre l'avant de sa voiture et les roues arrière de la voiture garée.
2) Calculer tan(KG;KF).

Correction

Les triangles KFG et KEH sont orthogonaux respéctivement en G et H donc

tan(x) =	FG	=	EH
	KG		KH

donc

80	=	135
KG		KG + 220

signifie 80(KG+220)=135KG
Signifie 135KG-80KG=80×220
donc KG=320cm.

2) Valeur aprochée de l'angle (KG ; KF).

tan(x) =	FG	=	1
	KG		4

signifie tan(KG ; KF)=0,25.
En utilisant une calculatrice scientifique
on obtient tan^-1(0,25)≃14,03°
ainsi (KG;KF)≃14,03°≃0,24rad.

Exercice 2 tp

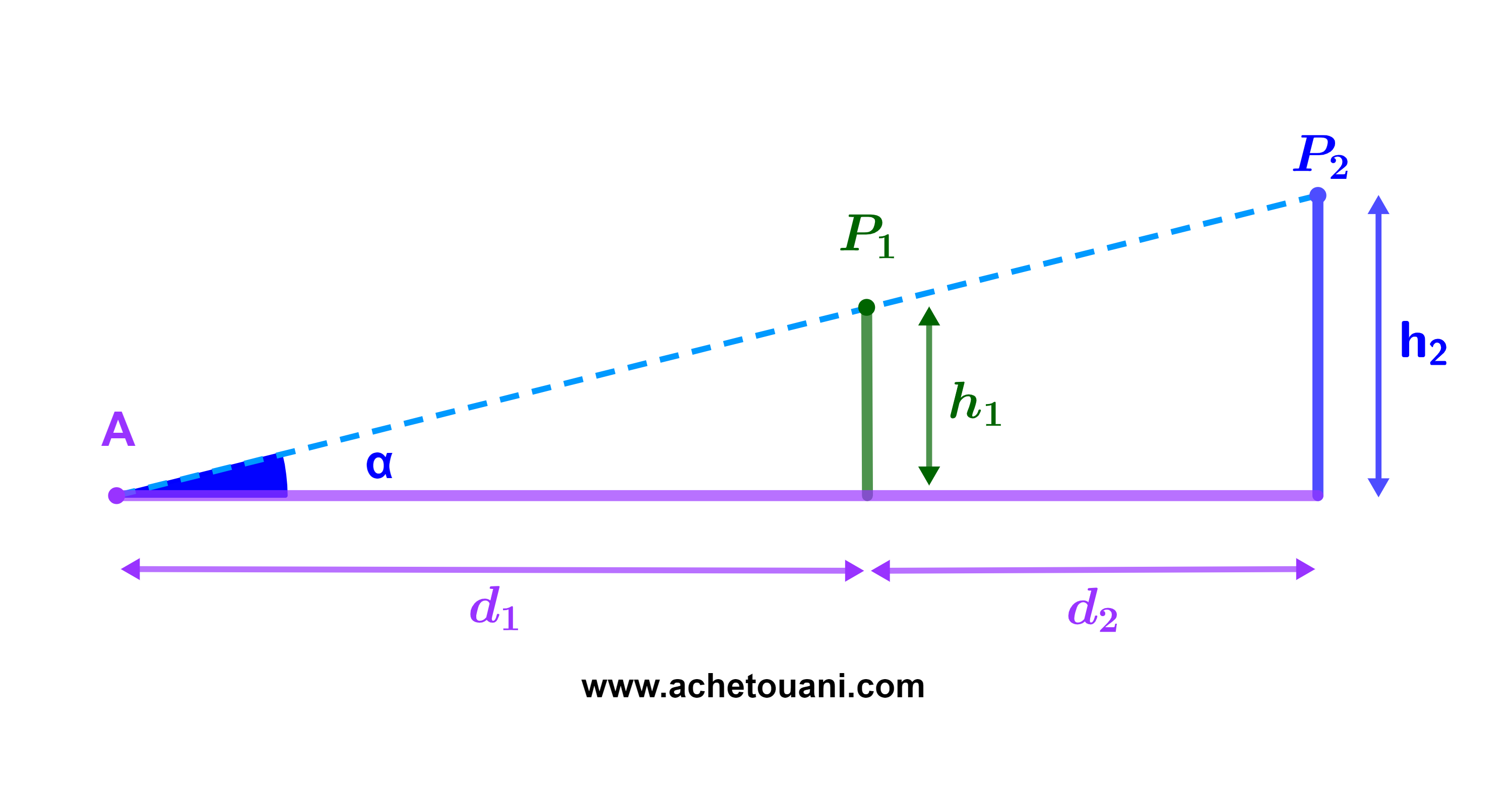
Soient P1 et P2 deux poteaux electriques.
d2=12m la distance entre eux.
Leurs sommets et un point A au sol soient sur la même droite (D).
Si le coefficient directeur de la droite (D) est 0,25 (ou encore tan(α)=0,25) et h1=5m est la hauteur du poteau P1.
1) Calculer d1 la distance entre A et P1.
2) Calculer h2 la hauteur du poteau P2.