Exercice 1 tp

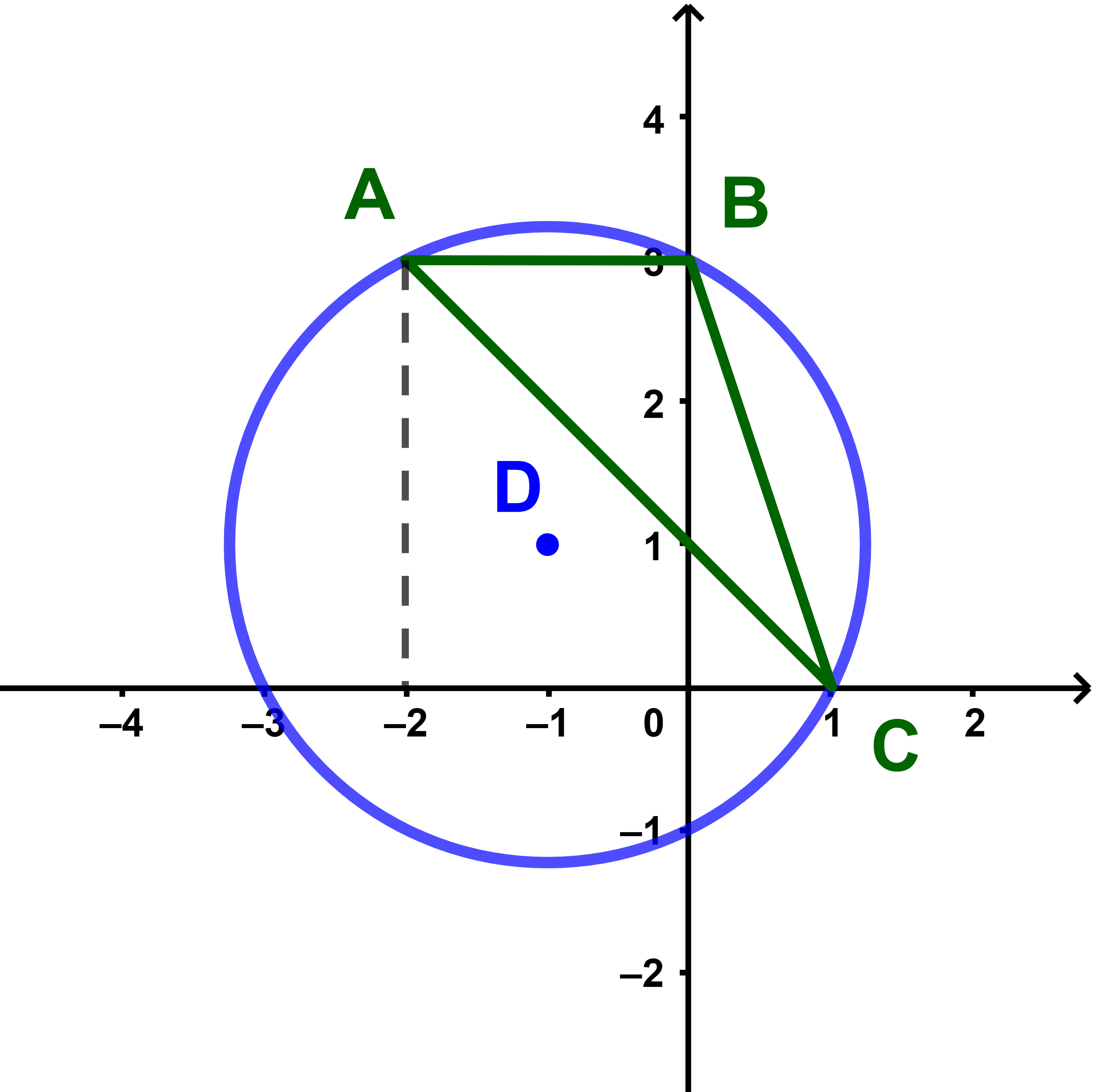
Le plan ℙ est rapporté à un repère orthonormé (O;i^→;j^→). On considère dans ℙ les points A(-2;3); B(0;3); C(1;0) et D(-1;1).
1) Représenter ces points dans le repère.
2) Montrer que D est le centre du cercle circonscrit au triangle (ABC).

3) Quelle est la nature du triangle (DBC)?
4) Calculer la mesure de l'angle (AC;AB)?

Exercice 2 tp

1) On considère le cercle suivant

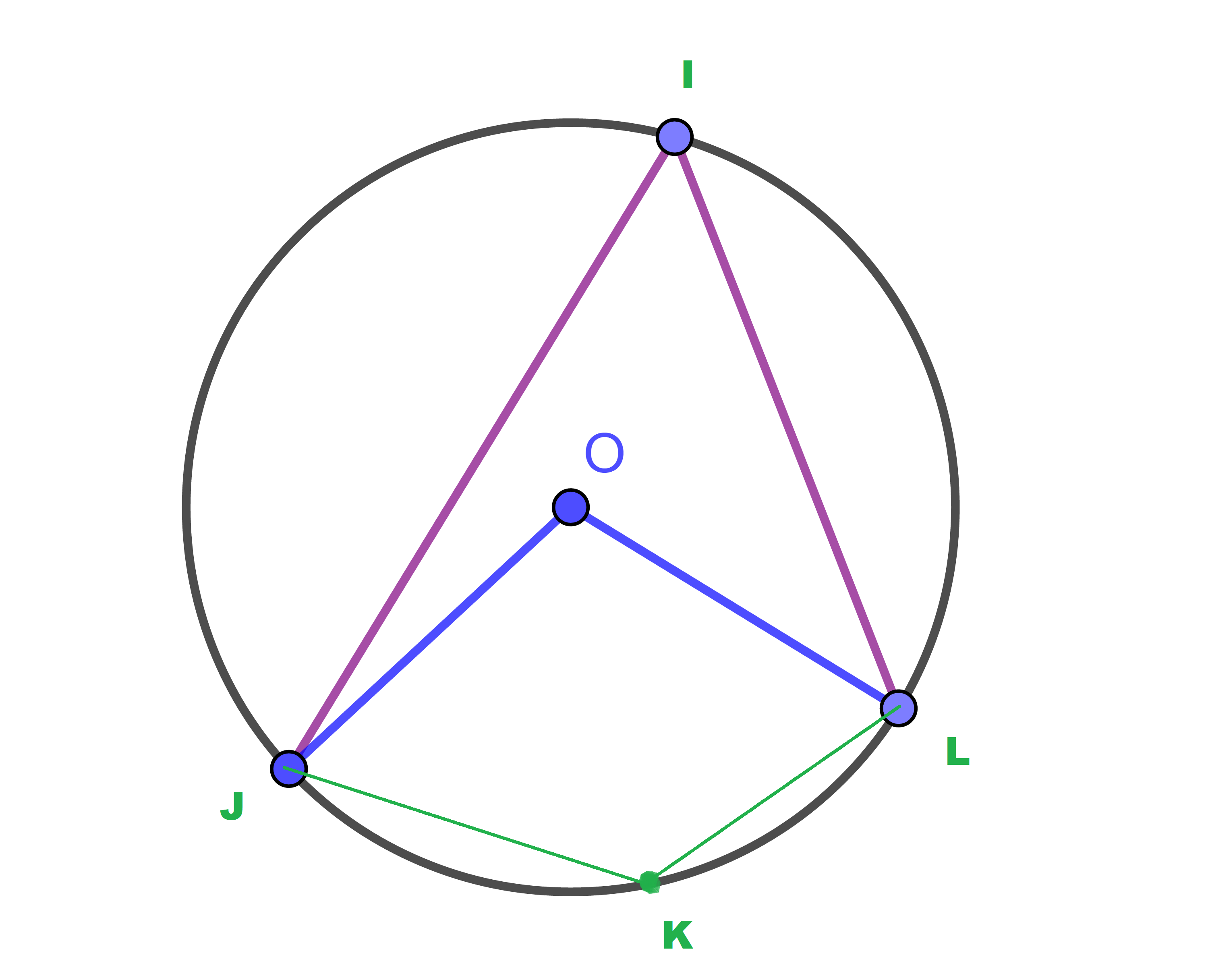
Si [LOJ]=110°
donner une mesure de l'angle [JKL].

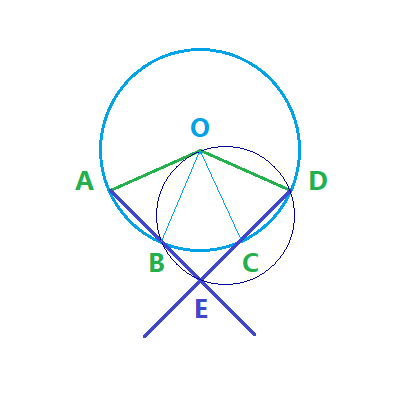
2) Soit A; B; C; D des points du cercle trigonométrique de centre O tel que les deux arcs arc(AB) et arc(CD) sont de même mesure et les deux-demi droites [AB) et [CD) se coupent au point E.
Construire la figure et montrer que O; B; E; D sont cocycliques.

Correction

1) On a [LOJ]=2[LIJ] et IJKL est circulaire
alors [LIJ]+[JKL]=π=180°
donc [JKL]=180°-55°=125°.

Rappel Le quadrilatère OBED est circulaire signifie
[DOB]+[BED]=π=180°.
ou
[EDO]+[OBE]=π=180°.

2) Pour cette question on utilise
[EDO]+[OBE]=π=180°

on pose x= [EDO] et y=[OBE]
(a) OD=OC donc le triangle OCD est isocèle de sommet O
ainsi 2x+[DOC]=π (relation 1).
(b) OA=OB donc le triangle OAB isocèle de sommet O ainsi 2[ABO]+[BOA]=π
et puisque arc(AB)=arc(CD)
alors [BOA]=[DOC].
On a donc 2[ABO]+[BOA]=π
signifie que 2[ABO]+[DOC]=π (relation 2).

On déduit de (1) et (2) que
2x+[DOC] = 2[ABO]+[DOC]
ou encore x=[ABO]
On a [ABO]+[OBE]=π
donc x+y=π et cela signifie que OBED est circulaire ou encore les points O; B; E; D sont cocycliques.