1- التناسبية

1.1 التناسب المباشر

1.1.1 انشطة

مثال 1
اتمم جدول التناسب التالي

المسافة ب كم	140	100	...	80
الزمن بالدقيقة	70	...	40	...

تصحيح

140	→	70 mn
100	→	t mn

يمكن تطبيق القاعدة الثلاثية اذن t=50 دقيقة.

140	→	70
80	→	t

اذن d=40 كم.
لدينا اذن

140	=	80
70		40

نقول ان الاعداد 140 ; 70 ; 80 ; 40 في هذا الترتيب متناسبة ونقول ايضا ان 140 و 80 متناسبة مع 70 و 40.

مثال 2
لدينا

24	= 3		12	= 3
8			4

اذن

24	=	12	= 3
8		4

نقول اذن 24 و 8 و 12 و 4 في هذا الترتيب متناسبة
ونقول ايضا 24 و 12 متناسبة مع 8 و 4
(مع احترام الترتيب ).

1.1.2 تعريف

نقول ان الاعداد غير المنعدمة d و c و b و a في هذا الترتيب متناسبة اذا

a	=	c
b		d
ad = bc او

امثلة
1) 15 ; 20 ; 7,5 ; 10 متناسبة
لأن 15.10=20.7,5 (150=150)
2) 24 ; 8 ; 30 ; 10 متناسبة
لان 24.10=8.30 (240=240).

ملاحظة
1) معادلة مستقيم مار من اصل المعلم تكتب على الشكل y=mx حيث m ميله.
ماذا يمكن القول عن اراتيب النقط M(a;b) ; N(c;d) لمستقيم (D) مار من اصل المعلم ((D): y=mx) ?

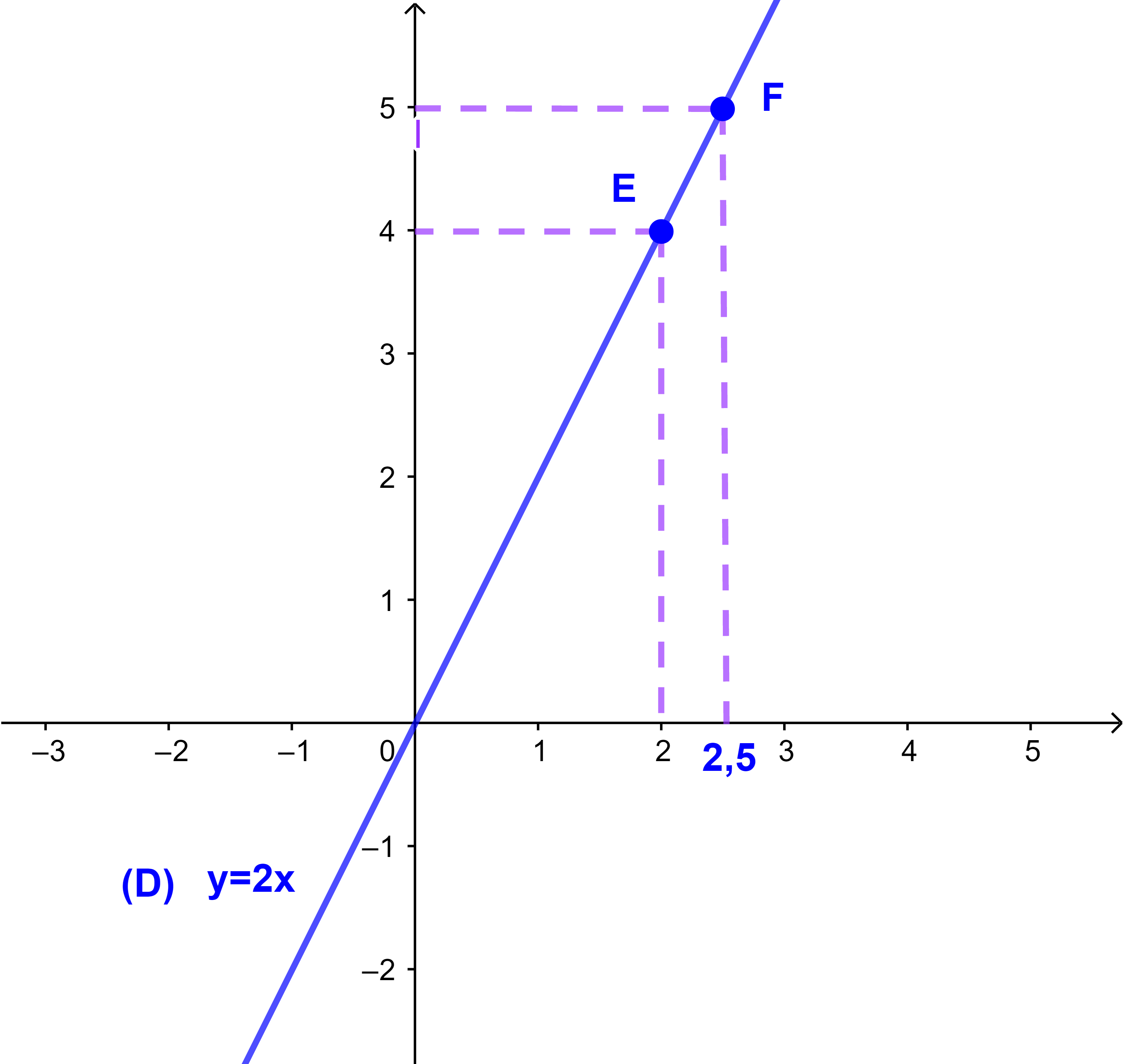
مثال نعتبر المستقيم (D): y=2x.
تحقق ان E(2 ; 4) و F(2,5 ; 5) تنتميان الى المستقيم (D).

تصحيح 1) نبين ان E تنتمي الى (D).
نضع x=2 و y=4 لذينا y=2x اذن 4=2.2 وهذا يعني ان الزوج (2;4) يحقق معادلة المستقيم (D) ومنه فان E تنتمي الى (D).
2) نبين ان F تنتمي الى (D).
نضع x=2,5 و y=5 لذينا y=2x اذن 5 = 2.2,5 وهذا يعني ان الزوج (2,5 ; 5) يحقق معادلة المستقيم (D) ومنه فان F تنتمي الى (D).

4.(2,5)=2.5=10 اذن 4 و 5 متناسبة مع 2 و 2,5.

نتائج أراتيب نقط مستقيم مار من أصل المعلم متناسبة مع الأفاصيل.
بتعبير آخر اذا كانت A(a;b) و B(c;d) تنتميان الى مستقيم معادلته تكتب على الشكل y=mx فان

b	=	d
a		c

مثال نعتبر المستقيم (D): y=4x النقطتان E(3;12) و F(2;8) تنتميان الى (D) اذن 12 و 8 متناسبة مع 3 و 2.

12	=	8
3		2