1- الاشتقاق في نقطة والاشتقاق على مجال

1.1 الاشتقاق في نقطة

1.1.1 المعامل الموجه لمستقيم تذكير

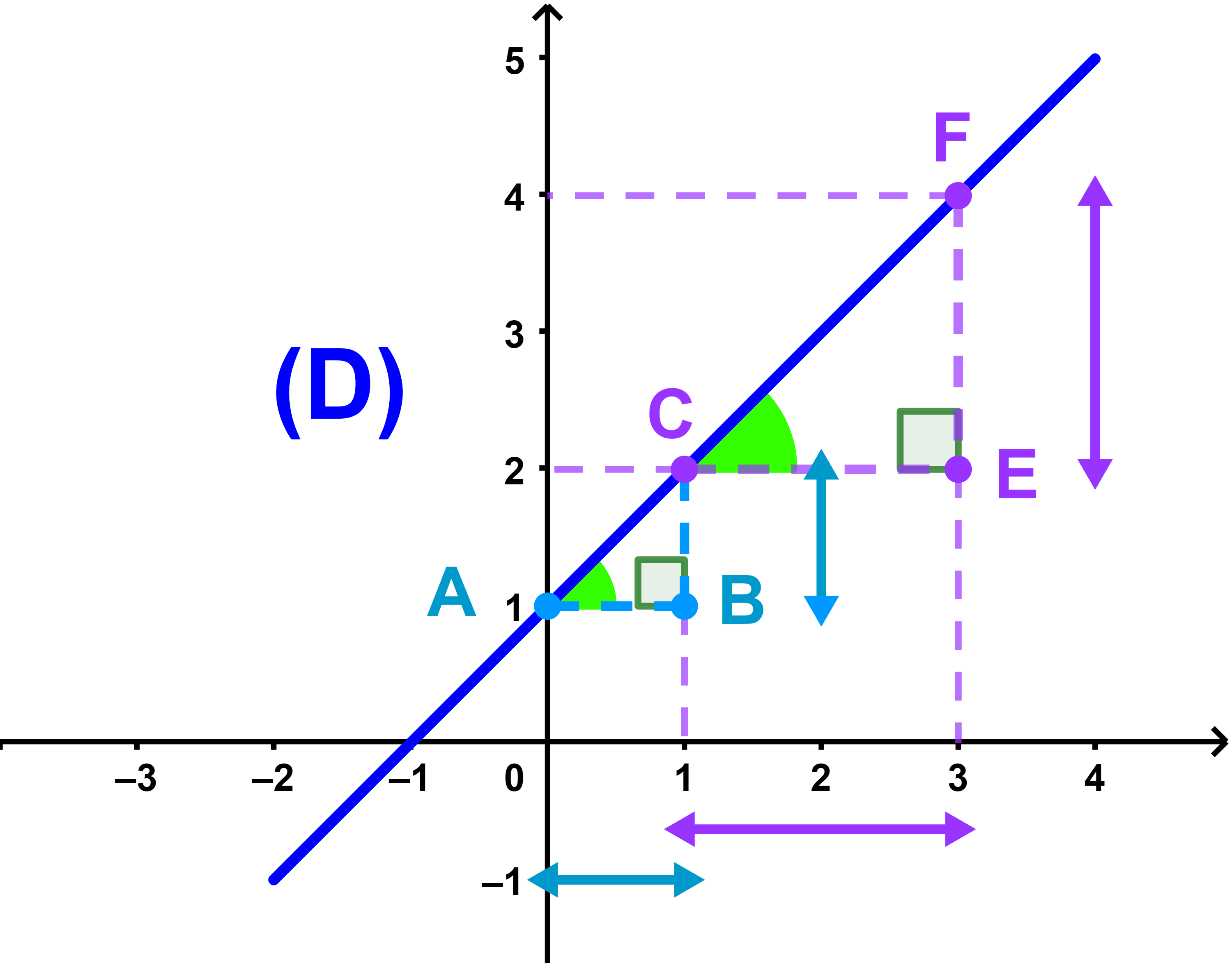
لتكن A و C نقطتين مختلفتين من مستقيم (D).
النسبة التالية

m =	yC - yA
	xC - xA

هي ميل أو المعامل الموجه للمستقيم (D).

y=mx+p هي المعادلة المختصرة للمستقيم (D).
p هو الارتوب عند الأصل.

1.1.2 تعريف

لتكن f دالة عددية معرفة على مجال I و a∈I نقول ان الدالة f قابلة للاشتقاق في نقطة a يعني يوجد عدد حقيقي L بحيث

lim x→a	f(x) - f(a)		= L
	x-a

العدد L يسمة العدد المشتق للدالة f في النقطة a ونرمز له ب f '(a).

lim x→a	f(x) - f(a)		= f '(a)
	x-a

1.1.3 التاويل الهندسي ومعادلة المماس

تقديم
لتكن f دالة قابلة للاشتقاق في a اذن

lim x→a	f(x) - f(a)		= f '(a)
	x-a

(C) المنحنى الممثل لها f في معلم (O;i^→;j^→) و A(a;f(a))∈(C). اذا كانت M(x;y)∈(C) فان العدد

f(x) - f(a)
x-a

هو المعامل الموجه للمستقيم (AM).

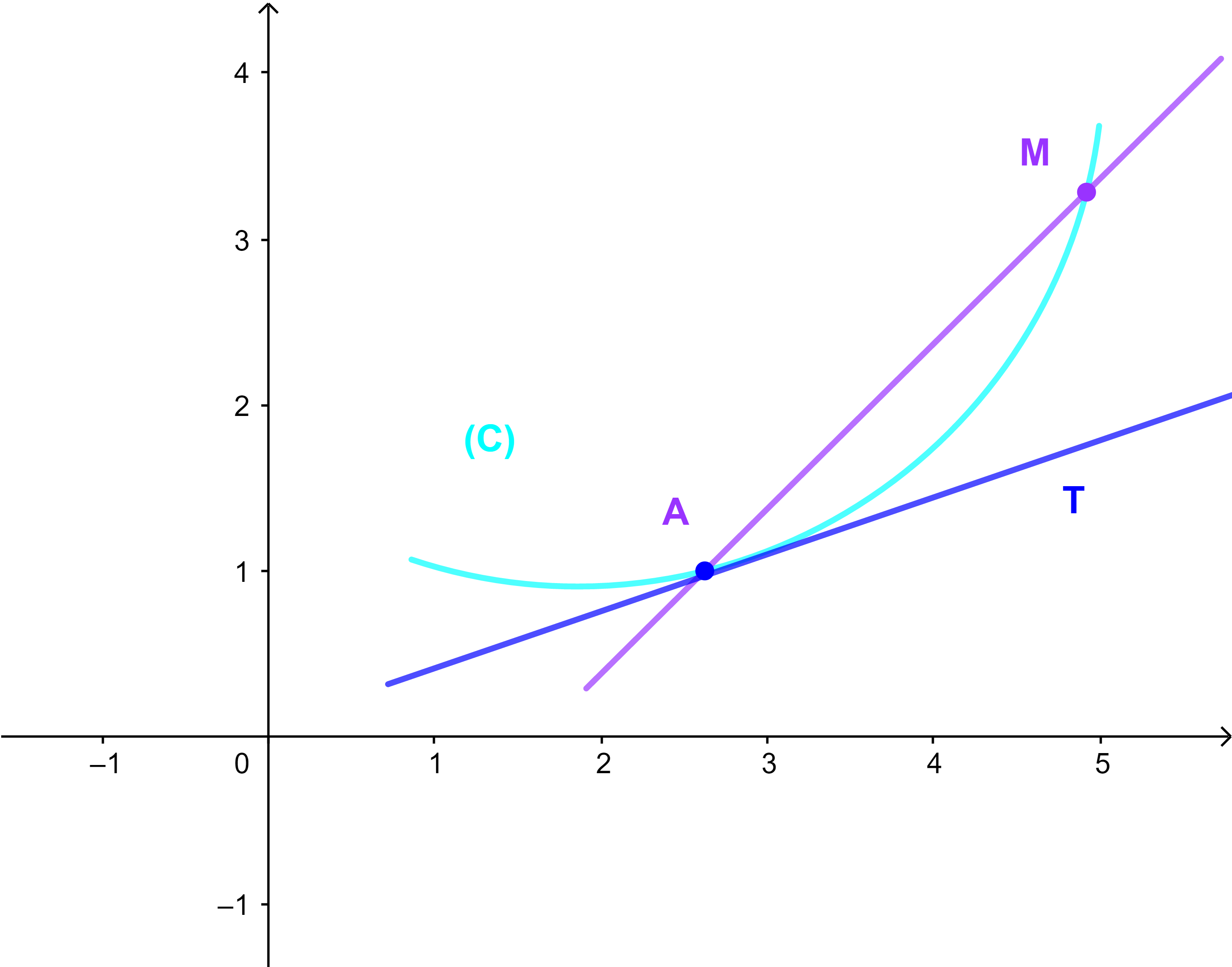
واذا كانت النقطة M تتغير وضعيتها على المنحنى الى ان تنطبق مع النقطة A فان المستقيم (AM) ياخذ وضعية المستقيم الوحيد (T) الذي يمس المنحنى في النقطة A=M.

ميل المستقيم (T) العدد

lim x→a	f(x) - f(a)		= f '(a)
	x-a

المستقيم (T) يسمى مماسا معادلته
y=f'(a)(x-a)+f(a).

خاصية وتعريف
لتكن f دالة عددية معرفة على مجال I حيث a∈I و (C) المنحنى الممثل للدالة f في معلم
اذا كانت f قابلة للاشتقاق في النقطة a فان (C) يقبل مماسا (T) في النقطة ذات الأفصول a ميله f'(a).

معادلة المماس (T) تكتب على الشكل
y=f'(a)(x-a)+f(a) وتسمى معادلة المماس (T).

مثال لتكن f دالة عددية بحيث f(x)=x².
1) بين أن f قابلة للاشتقاق في النقطة 5.
2) حدد معادلة المماس لمنحنى الدالة f في النقطة ذات الأقصول 5.

تصحيح
1) لدينا (5∈D) و f(5)=5²=25.

lim x→5	f(x) - f(5)	=	lim x→5	x² - 25
	x-5			x-5

=	lim x→5	(x-5)(x+5)
		x-5
=	lim x→5	x + 5 = 10

اذن الدالة f قابلة للاشتقاق في 5 وعددها المشتق عند 5 هو f'(5)=10.
بما أن الدالة f قابلة للاشتقاق في 5 فان المنحنى (C) يقبل مماسا (T) معادلته تكتب على الشكل
y=f'(5)(x-5)+f(5)=10(x-5)+25
وبالتالي معادلة المماس (T): y=10x-25.