3.2 مطارف دالة قابلة للاشتقاق

3.2.1 القيمة الدنيا والقيمة القصوى تذكير

تعريف 1
f دالة عددية معرفة على مجال I القيمة الدنيا لدالة عددية f على المجال I اصغر قيمة صور عناصر المجال I بواسطة الدالة f.
وبتعبير آخر
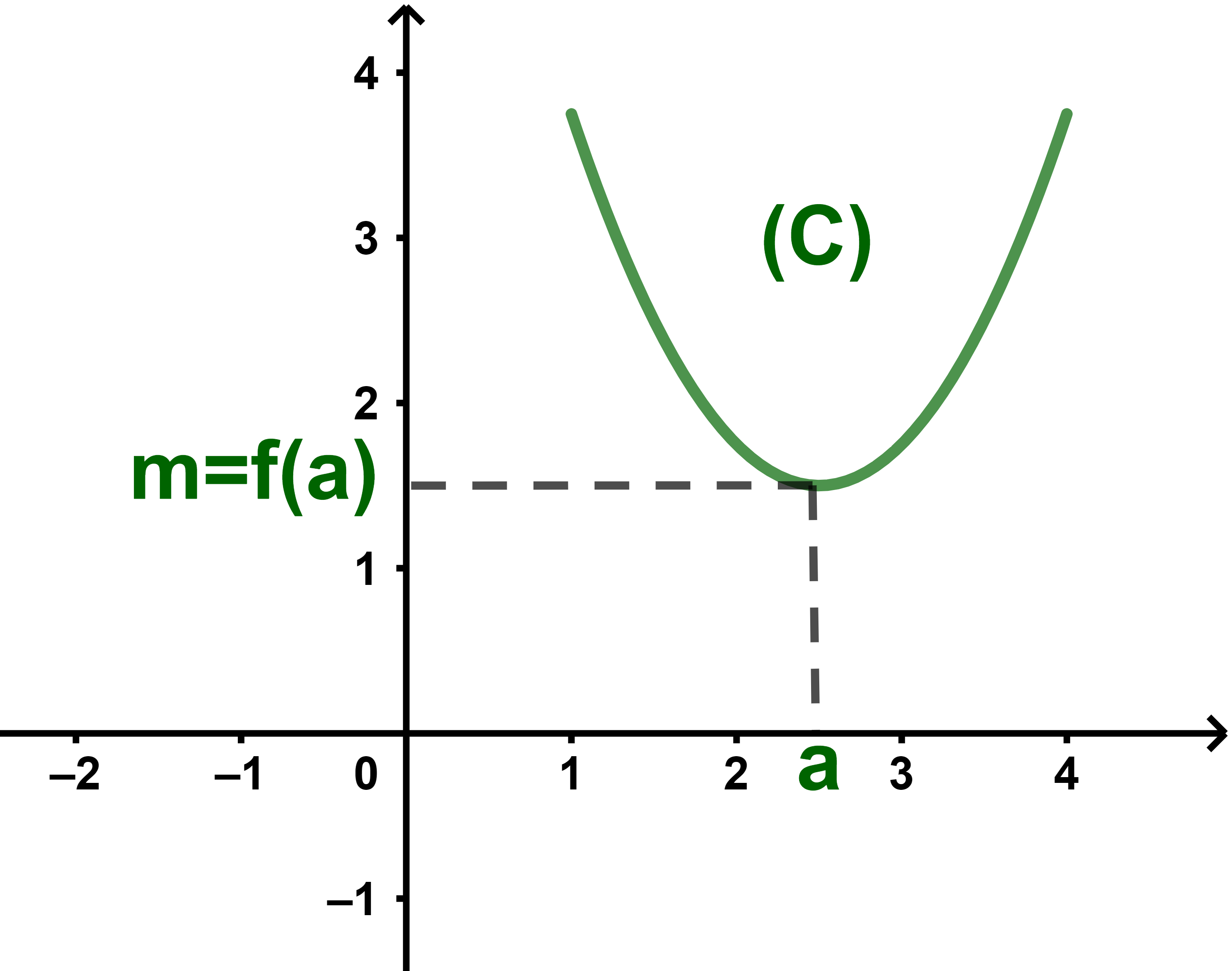
m قيمة دنيا ل f على I اذا وجد عدد حقيقي a في المجال I بحيث لكل x∈I لدينا f(x)≥m=f(a).

تعريف 2
لتكن f دالة عددية معرفة على مجال I. القيمة القصوى لدالة عددية f على المجال I اكبر قيمة صور عناصر المجال I بواسطة الدالة f.
وبتعبير آخر
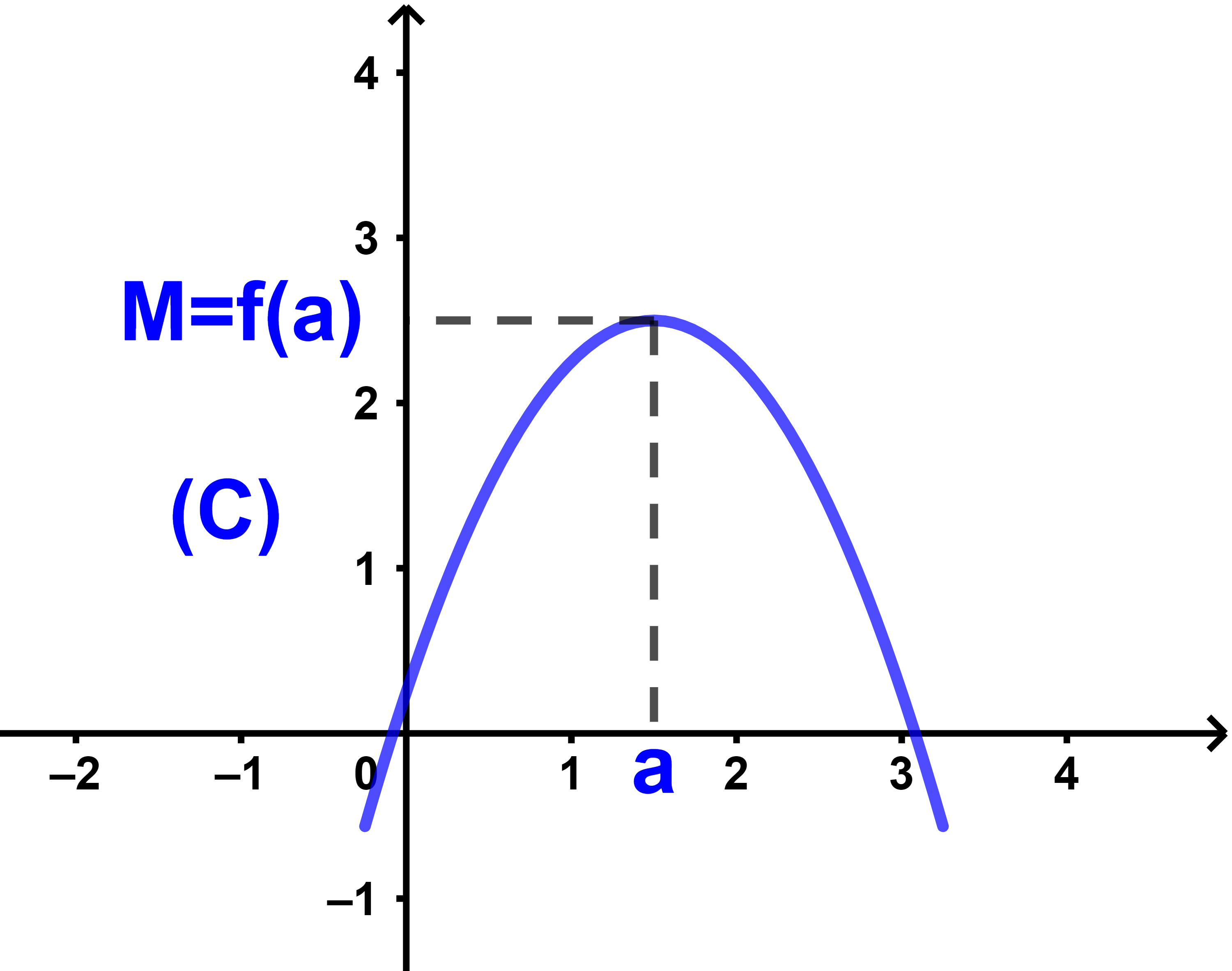
M قيمة قصوى ل f على I اذا وجد عدد حقيقي a في المجال I بحيث لكل x∈I لدينا f(x)≤M=f(a).

تعريف 3
لتكن f دالة عددية معرفة على مجال I و a∈I.
نقول ان f(a) مطراف للدالة f على I اذا كان قيمة قصوى او قيمة دنيا للدالة f على المجال I.

3.2.2 خاصية 1

لتكن f دالة قابلة للاشتقاق على I و a∈I.
اذا كانت f تقبل مطرافا عند a فان f'(a)=0.

ملاحظة
العكس ليس دائما صحيحا ناخذ مثالا f(x)=x³.
لدينا f'(x)=3x² اذن f'(0)=0
ولكن f لا تقبل مطرافا عند 0 لان 0 ليس قيمة دنيا وليس قيمة قصوى.

3.2.3 خاصية 2

لتكن f دالة قابلة للاشتقاق على مجال I و a∈I.
اذا كانت f' تنعدم في a وتتغير اشارتها بجوار a فان f(a) مطراف للدالة f.